2023年北师大版数学八年级下学期期末模拟试卷（4）

试卷更新日期：2023-05-31 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O，下列等式一定正确的是（）

A、 $A D = C D$ B、 $A C = B D$ C、 $A B = C D$ D、 $A D = A O$

查看试题解析
3. 如图， $Δ A B C$ 中， $A C = 6$ ， $B C = 8$ ， $A B = 10$ ． $A D$ 为 $Δ A B C$ 的角平分线， $C D$ 的长度为（）

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{10}{3}$

查看试题解析
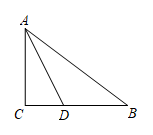4. 下列因式分解正确的是（）

A、x²-y²＝（x-y）² B、a²+a+1＝（a+1）² C、2xy-6x＝2x（y-3） D、a²+4a+21＝a（a+4）+21

查看试题解析
5. 若不等式组 ${\begin{array}{l} x > a \\ x \geq - 3 \end{array}$ 的解集为 $x > a$ ，则下列各式正确的是（）

A、 $a < 3$ B、 $a \leq 3$ C、 $a > - 3$ D、 $a \geq - 3$

查看试题解析
6. 如图， $∠ C = 90 °$ ，将直角三角形 $A B C$ 沿着射线 $B C$ 方向平移 $5 c m$ ，得三角形 $A^{'} B^{'} C^{'}$ $，$ 已知 $B C = 3 c m ， A C = 4 c m$ ，则阴影部分的周长为（）

A、 $16 c m$ B、 $18 c m$ C、 $20 c m$ D、 $22 c m$

查看试题解析
7. 下列各分式正确的是（）

A、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ B、 $\frac{x^{6}}{x^{3}} = x^{2}$ C、 $\frac{x^{2} - 5 x}{x^{2} - 10 x + 25} = \frac{x}{x - 5}$ D、 $- \frac{x + 1}{x - y} = \frac{x - 1}{x - y}$

查看试题解析
8. 根据图象，可得关于x的不等式k₁x＜k₂x+b的解集是（）

A、x＜2 B、x＞2 C、x＜3 D、x＞3

查看试题解析
9. 下面是教师出示的作图题．
已知：线段a，h，小明用如图所示的方法作 $△ A B C$ ，使 $A B = a$ ， $A B$ 上的高 $C P = h$ ．
作法：①作射线 $A M$ ，以点A为圆心、※为半径画弧，交射线 $A M$ 于点B；②分别以点A，B为圆心、△为半径画弧，两弧交于点D，E；③作直线 $D E$ ，交 $A B$ 于点P；④以点P为圆心、 $\oplus$ 为半径在 $A M$ 上方画弧，交直线 $D E$ 于点C，连接 $A C$ ， $B C$ ．
对于横线上符号代表的内容，下列说法错误的是（）

A、※代表“线段a的长” B、△代表“任意长” C、△代表“大于 $\frac{1}{2} a$ 的长” D、 $\oplus$ 代表“线段h的长”

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C$ ， $M$ ， $N$ 分别是 $A B$ ， $A C$ 的中点， $D$ ， $E$ 为 $B C$ 上的点，连接 $D N$ ， $E M$ ．若 $A B = 13$ cm， $B C = 10$ cm， $D E = 5$ cm，则图中阴影部分面积为（）

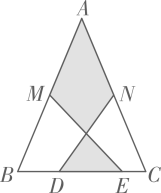A、25cm² B、35cm² C、30cm² D、42cm²

查看试题解析

二、填空题（每空3分，共15分）

11. 若式子 $\frac{\sqrt{x + 3}}{x - 2}$ 有意义，则x的取值范围是

查看试题解析
12. 分解因式 $2 x^{2} - 8 x + 8 =$ ．

查看试题解析
13. 如图， $∠ B A C = 30 °$ ， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ D E$ ，已知 $D E = 1$ ，则 $A E =$ .

查看试题解析
14. 如图，已知 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 280 °$ ，那么 $∠ 5$ 的度数为

查看试题解析
15. 已知a和b两个有理数，规定一种新运算“*”为：a*b＝ $\frac{a - b}{a + b}$ （其中a+b≠0），若m* $(- \frac{5}{4})$ ＝ $- \frac{3}{5}$ ，则m＝.

查看试题解析

三、作图题（共7分）

16. 如图所示的正方形网格中，△ABC 的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：

（1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△ $A B_{1} C_{1}$ ，画出△ $A B_{1} C_{1}$ ；
（2）作出△ABC关于坐标原点O成中心对称的△ $A_{2} B_{2} C_{2}$ .
（3）作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△ $A_{2} B_{2} C_{2}$ 的内部（不含落在△ $A_{2} B_{2} C_{2}$ 的边上），请直接写出x的取值范围 ▲ .（提醒：每个小正方形边长为1个单位长度）

查看试题解析

四、解答题（共6题，共48分）

17. 解不等式（组）.

(1)、解不等式： $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} > 1$ ，

(2)、解不等式组 ${\begin{array}{l} x - 4 < 3 (x - 2) \\ \frac{1 + 2 x}{3} + 1 \geq x \end{array}$ ，并把它的解集表示在数轴上.

查看试题解析
18.

(1)、计算： $6 + (\sqrt{5} + 1) (\sqrt{5} - 1)$ ．

(2)、下面是夏红同学对题目的计算过程，请认真阅读并完成相应的任务．
题目：已知 $x = \sqrt{2}$ ，求 $x + 1 - \frac{x^{2}}{x - 1}$ 的值．

原式 $= \frac{(x + 1) (x - 1) - x^{2}}{x - 1}$ 第一步

$= \frac{x^{2} - 1 - x^{2}}{x - 1}$      第二步

$= \frac{- 1}{x - 1}$         第三步

所 $x = \sqrt{2}$ 代入上式，得

原式 $= \frac{- 1}{\sqrt{2} - 1}$      第四步

$= \frac{- 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$    第五步

$= - 1$ ．         第六步

任务一：填空：

①在化简步骤中，第步是进行分式的通分．

②第步开始出错，这一错误的原因是．

任务二：请直接写出该题计算后的正确结果．

查看试题解析
19. 如图，在 $▱ A B C D$ 中，E，F是对角线 $A C$ 上的两点，且 $A E = C F$ ．

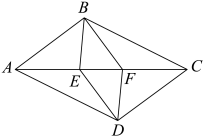(1)、求证：四边形 $B E D F$ 是平行四边形；

(2)、若 $A B ⊥ B F$ ， $A B = 8$ ， $B F = 6$ ， $A C = 16$ ．求线段 $E F$ 长．

查看试题解析
20. 我们学习了一元一次不等式（组）的解法，请阅读学习一元二次不等式的解题思想方法，并以此解决后面的问题．
课题学习：如何解一元二次不等式？
例题：解一元二次不等式 $x^{2} - 4 > 0$ ．
解：将 $x^{2} - 4$ 分解因式
$x^{2} - 4 = (x + 2) (x - 2)$
∵ $x^{2} - 4 > 0$
∴ $(x + 2) (x - 2) > 0$
根据有理数的乘法法则：“两数相乘，同号得正”，
则有：（1） ${\begin{array}{l} x + 2 > 0 \\ x - 2 > 0 \end{array}$ 或（2） ${\begin{array}{l} x + 2 < 0 \\ x - 2 < 0 \end{array}$
解不等式组（1）得： $x > 2$
解不等式组（2）得： $x < - 2$
∴ $(x + 2) (x - 2) > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ．
即：一元二次不等式 $x^{2} - 4 > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ．
课题总结：解一元二次不等式的过程，体现了数学的化归思想及分类讨论思想．
问题解决：

(1)、解一元二次不等式 $x^{2} - 3 x > 0$

(2)、类比一元二次不等式的解题思想方法，直接写出分式不等式 $\frac{2 x + 1}{x - 5} < 0$ 的解集为：．

查看试题解析
21. 某服装店老板到厂家选购A、B两种品牌的夏季服装，每袋A品牌服装进价比B品牌服装每袋进价多25元，若用4000元购进A种服装的数量是用1500元购进B种服装数量的2倍．

(1)、求A、B两种品牌服装每套进价分别是多少元？

(2)、若A品牌服装每套售价为150元，B品牌服装每套售价为100元，服装店老板决定一次性购进两种服装共100套，两种服装全部售出后，要使总的获利不少于3500元，则最少购进A品牌服装多少套？

查看试题解析
22. 如图，在Rt△ACB中，∠ACB=90°，D为AB中点，点E在直线BC上(点E不与点B，C重合)，连接DE，过点D作DF⊥DE交直线AC于点F，连接EF．

(1)、如图(a)，当点F与点A重合时，请直接写出线段EF与BE的数量关系：

(2)、如图(b)，当点F不与点A重合时，证明：AF²+BE²=EF²；

(3)、若AC=5，BC=3，EC=1，请直接写出线段AF的长．

查看试题解析