2023年北师大版数学八年级下学期期末模拟试卷(2)
试卷更新日期:2023-05-31 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 要使分式有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列标志中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、4. 若 , 则下列关系式不成立的是( )A、 B、 C、 D、5. 如图,中,是的平分线,则周长为( )
3. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、4. 若 , 则下列关系式不成立的是( )A、 B、 C、 D、5. 如图,中,是的平分线,则周长为( ) A、20 B、24 C、32 D、406. 如果把中的x与y都扩大为原来的5倍,那么这个代数式的值( )A、不变 B、扩大为原来的5倍 C、缩小为原来的 D、扩大为原来的10倍7. 下列不能判断一个四边形是平行四边形的是( )A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等,且另一组对边平行的四边形8. 3月4日,太原市住建局宣布,本市2022年计划改造老旧小区604个,涉及户数11.6万户.某小区计划在改造时给80户住户安装天然气,住户需共同承担整体初装费30000元,另需缴纳入户费500元/户.根据惠民政策,政府给予该小区住户一定的补贴,这样平均每户的实际费用不超过800元.若设政府给每户的补贴为x元,则x满足的不等式为( )
A、20 B、24 C、32 D、406. 如果把中的x与y都扩大为原来的5倍,那么这个代数式的值( )A、不变 B、扩大为原来的5倍 C、缩小为原来的 D、扩大为原来的10倍7. 下列不能判断一个四边形是平行四边形的是( )A、一组对边平行且相等的四边形 B、两组对边分别相等的四边形 C、对角线互相平分的四边形 D、一组对边相等,且另一组对边平行的四边形8. 3月4日,太原市住建局宣布,本市2022年计划改造老旧小区604个,涉及户数11.6万户.某小区计划在改造时给80户住户安装天然气,住户需共同承担整体初装费30000元,另需缴纳入户费500元/户.根据惠民政策,政府给予该小区住户一定的补贴,这样平均每户的实际费用不超过800元.若设政府给每户的补贴为x元,则x满足的不等式为( ) A、 B、 C、 D、9. 如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC=8,BD=12,E、F分别为BO、CO上两点,且BE=CF,连接AE、DF,则△ABE与△CDF的面积比为( )
A、 B、 C、 D、9. 如图,平行四边形ABCD中,对角线AC、BD交于点O,且AC=8,BD=12,E、F分别为BO、CO上两点,且BE=CF,连接AE、DF,则△ABE与△CDF的面积比为( )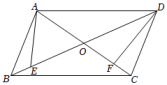 A、 B、 C、 D、10. 如图已知中, , , 边上的中线 , 则的面积为( ) .
A、 B、 C、 D、10. 如图已知中, , , 边上的中线 , 则的面积为( ) . A、30 B、130 C、60 D、120
A、30 B、130 C、60 D、120二、填空题(每空3分,共15分)
-
11. 分解因式: .12. 已知一个多边形的每一个内角都是140°,则这个多边形的边数为13. 如图,直线和相交于点 , 则不等式的解集为.
 14. 如图,平行四边形ABCD的周长是12cm,对角线AC,BD相交于点O,OE⊥BD交AD于点E;则△ABE的周长为cm.
14. 如图,平行四边形ABCD的周长是12cm,对角线AC,BD相交于点O,OE⊥BD交AD于点E;则△ABE的周长为cm. 15. 如图,在中,、分别是、的中点, , 是上一点,连结、 ,若 , , 则的长为 .
15. 如图,在中,、分别是、的中点, , 是上一点,连结、 ,若 , , 则的长为 .
三、计算题(共2题,共13分)
-
16. 解下列不等式组,并在数轴上表示出不等式组的解集:(1)、(2)、17. 先化简: , 然后在-2,-1,2三个数中给a选择一个你喜欢的数代入求值.
四、作图题(共9分)
-
18. 如图,△ABC的三个顶点的坐标分别为A (-3,1),B(0,3),C(0,1).

⑴将△ABC向下平移3个单位长度,得△A'B'C,画出△A'B'C;
⑵写出点B'的坐标:
⑶将△ABC以点C为旋转中心顺时针旋转90°,得△A"B"C,画出△A"B"C.
五、解答题(共4题,共33分)
-
19. 某汽车网站对两款售价相同,续航里程相同的汽车做了一次评测,一款为燃油车,另一款为纯电新能源车.得到相关数据如下:
燃油车
纯电新能源车
油箱容积:48升
电池容量:90千瓦时
油价:8元/升
电价:0.6元/千瓦时
续航里程:a千米
续航里程:a千米
每千米行驶费用:元
每千米行驶费用:____元
(1)、用含a的代数式表示新能源车的每千米行驶费用元(结果为最简);(2)、若燃油车每千米行驶费用比纯电新能源车多0.55元.①请分别求出这两款车的每千米行驶费用;
②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元.问:每年行驶里程超过多少千米时,新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
20. 在中, , D是斜边上的一点,作 , 垂足为E,延长到F,连结 , 使. (1)、求证:四边形是平行四边形;(2)、连接 , 若平分 , , 求四边形的面积.21. 入夏以来,居民用电量持续攀升.为鼓励居民节约用电,某市从6月起,启用夏季收费政策,该政策有两种用电收费方法:
(1)、求证:四边形是平行四边形;(2)、连接 , 若平分 , , 求四边形的面积.21. 入夏以来,居民用电量持续攀升.为鼓励居民节约用电,某市从6月起,启用夏季收费政策,该政策有两种用电收费方法:分时电表
普通电表
峰时(9:00﹣22:00)
谷时(22:00到次日9:00)
电价0.62元/kW•h
电价0.82元/kW•h
电价0.42元/kW•h
小亮所在数学学习小组提出以下问题:家庭使用分时电表是不是一定比普通电表合算呢?他们进行了以下研究:
(1)、设某家庭某月用电总量akW•h(a为常数),其中峰时用电xkW•h,用分时电表计价时总价为y1元,普通计价时总价为y2元.求出y1、y2与用电量之间的关系式;(2)、请判断使用分时电表是不是一定比普通电表更合算?(3)、小亮家所在小区的电表今年已经全部换成分时电表.若小亮家6月份用电250kW•h,其中峰时用电100kW•h,试用(2)中的结论,分析小亮家使用分时电表是否合算.22. 在中, , , 将绕点B顺时针旋转得到 , 交于点E,分别交 , 于点D、F. (1)、如图1,在旋转过程中,猜想线段与满足的数量关系并加以证明;(2)、如图2,当时,试判断四边形的形状,并证明;(3)、在(2)的条件下,求线段的长.
(1)、如图1,在旋转过程中,猜想线段与满足的数量关系并加以证明;(2)、如图2,当时,试判断四边形的形状,并证明;(3)、在(2)的条件下,求线段的长.
-