浙江省杭州市淳安县2022-2023学年九年级下学期期中数学试题
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列四个数中,最小的数是( )A、 B、 C、1 D、02. 苹果的单价为元/千克,香蕉的单价为元/千克,买2千克苹果和3千克香蕉共需( )A、元 B、元 C、元 D、元3. 袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有和四种规格,小朦同学已经取了和两根木棍,那么第三根木棍不可能取( )A、 B、 C、 D、4. 《九章算术》中记载了一个问题,大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的 , 那么乙也共有钱50.问:甲,乙两人各带了多少钱?设甲,乙两人持钱的数量分别为x,y,则可列方程组为( )A、 B、 C、 D、5. 千岛湖某青年志愿者协会的10名志愿者,一周的社区志愿服务时间如表所示:
时间/h
2
3
4
5
6
人数
1
3
2
3
1
关于志愿者服务时间的描述正确的是( )
A、众数是6 B、中位数是4 C、平均数是3 D、方差是16. 在中, , 、、所对的边分别是a、b、c.则下列各式中,正确的是( )A、 B、 C、 D、7. 已知一次函数 , 其中y的值随x的值增大而减小,则m的取值范围是( )A、 B、 C、 D、8. 如图,矩形中, , , M为线段上一动点,于点P,于点Q,则的最小值是( ) A、 B、3 C、 D、9. 已知点、是二次函数图象上的两个点,若当时,y随x的增大而减小,则m的取值范围是( )A、 B、 C、 D、10. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
A、 B、3 C、 D、9. 已知点、是二次函数图象上的两个点,若当时,y随x的增大而减小,则m的取值范围是( )A、 B、 C、 D、10. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )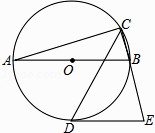 A、 B、2 C、2 D、3
A、 B、2 C、2 D、3二、填空题
-
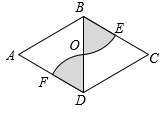
11. 计算: .12. 一组数据: , 则这组数据的方差是 .13. 如图,菱形中,分别以点B,D为圆心,以长为半径画弧,分别交边于点E,F.若 , 则图中阴影部分的面积为 . (结果不取近似值)
 14. 在△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,tan∠BPC= .
14. 在△ABC中,AB=AC=5,BC=8,若∠BPC=∠BAC,tan∠BPC= . 15. 已知函数y与自变量x的部分对应值如表:
15. 已知函数y与自变量x的部分对应值如表:x
…
-5
-2
2
5
…
y
…
-2
m
5
n
…
下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,且图象开口向下,则 . 其中正确的是 . (填写正确的序号)
16. 如图,在矩形中, , 点F、G分别在边上,沿将四边形翻折得到四边形 , 且点E落在边上,交于点H.若 , 则的长为.
三、解答题
-
17. 用消元法解方程组时,两位同学的消元方法如下:
小吴解法:由 , 得 .
小严解法:由②,得③
把①代入③,得 .
(1)、上述两位同学的消元过程是否有误,请判断.(2)、请选择一种你喜欢的方法,解出方程组.18. 千岛湖某学校想知道学生对“大下姜”,“沪马公园”,“月光之恋”等旅游景点的了解程度,随机抽查了部分学生进行问卷调查,问卷有四个选项(每位被调查的学生必须且只能选一项):A.不知道,B.了解较少,C.了解较多,D.十分了解.将问卷调查的结果绘制成如下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题: (1)、本次调查了多少名学生?(2)、根据调查信息补全条形统计图;(3)、该校共有1800名学生,请你估计“十分了解”的学生共有多少名?(4)、在被调查“十分了解”的学生中,有四名同学普通话较好,他们中有2名男生和2名女生,学校想从这四名同学中任选两名同学,做家乡旅游品牌的宣传员,请你用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.19. 如图,在方格子中,有一条线段 , 两个端点在格点上,请利用网格和无刻度的直尺作图,保留痕迹,不写作法.
(1)、本次调查了多少名学生?(2)、根据调查信息补全条形统计图;(3)、该校共有1800名学生,请你估计“十分了解”的学生共有多少名?(4)、在被调查“十分了解”的学生中,有四名同学普通话较好,他们中有2名男生和2名女生,学校想从这四名同学中任选两名同学,做家乡旅游品牌的宣传员,请你用列表法或画树状图法,求出被选中的两人恰好是一男一女的概率.19. 如图,在方格子中,有一条线段 , 两个端点在格点上,请利用网格和无刻度的直尺作图,保留痕迹,不写作法. (1)、如图1中,在线段上作出一点C,使得;(2)、如图2中,在线段上作出一点D,使得 .20. 已知一次的图象与反比例函数的图象相交.(1)、判断是否经过点 .(2)、若的图象过点 , 且 .
(1)、如图1中,在线段上作出一点C,使得;(2)、如图2中,在线段上作出一点D,使得 .20. 已知一次的图象与反比例函数的图象相交.(1)、判断是否经过点 .(2)、若的图象过点 , 且 .①求的函数表达式.
②当时,比较 , 的大小.
21. 如图所示,的顶点、在⊙上,顶点在⊙外,边与⊙相交于点 , , 连接、 , 已知.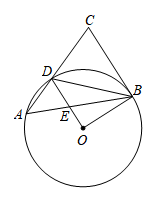 (1)、求证:直线是⊙的切线;(2)、若线段与线段相交于点 , 连接.
(1)、求证:直线是⊙的切线;(2)、若线段与线段相交于点 , 连接.①求证:;
②若 , 求⊙的半径的长度.
