广东省广州市黄埔广附教育集团联考2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列值中,能满足在实数范围内有意义的是( )A、x=2019 B、x=2020 C、x=2021 D、x=20224. 下列命题中是假命题的是( )A、△ABC中,若∠B=∠C-∠A,则△ABC是直角三角形 B、△ABC中,若a2=(b+c)(b-c),则△ABC是直角三角形 C、△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形 D、△ABC中,若a∶b∶c=5∶4∶3,则△ABC是直角三角形5. 《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为 尺,则可列方程为( )A、 B、 C、 D、6. 如图,平行四边形ABCD的对角线AC、BD相交于点O,已知AD=5,BD=8,AC=6,则△OBC的面积为( )
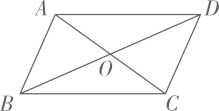 A、5 B、6 C、8 D、127. 已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A+∠B=180°8. 下列命题的逆命题是真命题的是( )A、如果两个角是直角,那么它们相等 B、如果两个实数相等,那么它们的平方相等 C、如果一个四边形是菱形,那么它的四条边都相等 D、如果一个四边形是矩形,那么它的对角线相等9. 如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长( )
A、5 B、6 C、8 D、127. 已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是( )A、AB=CD B、AD=BC C、AD∥BC D、∠A+∠B=180°8. 下列命题的逆命题是真命题的是( )A、如果两个角是直角,那么它们相等 B、如果两个实数相等,那么它们的平方相等 C、如果一个四边形是菱形,那么它的四条边都相等 D、如果一个四边形是矩形,那么它的对角线相等9. 如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长( ) A、只与AB、CD的长有关 B、只与AD、BC的长有关 C、只与AC、BD的长有关 D、与四边形ABCD各边的长都有关10. 如图,平面内三点A、B、C, , ,以 为对角线作正方形 ,连接 ,则 的最大值是 ( )
A、只与AB、CD的长有关 B、只与AD、BC的长有关 C、只与AC、BD的长有关 D、与四边形ABCD各边的长都有关10. 如图,平面内三点A、B、C, , ,以 为对角线作正方形 ,连接 ,则 的最大值是 ( ) A、5 B、7 C、 D、
A、5 B、7 C、 D、二、填空题
-
11. 如图所示:数轴上点A所表示的数为a,则a的值是 .
 12. 平行四边形一个内角的角平分线分对边为3和4两部分,则平行四边形的周长为 .13. 使 成立的条件是.14. 由于四边形具有不稳定性,如图,将正方形ABCD向下挤压变形后得到菱形 . 若 , 则菱形与原正方形ABCD的面积之比为
12. 平行四边形一个内角的角平分线分对边为3和4两部分,则平行四边形的周长为 .13. 使 成立的条件是.14. 由于四边形具有不稳定性,如图,将正方形ABCD向下挤压变形后得到菱形 . 若 , 则菱形与原正方形ABCD的面积之比为 15. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的面积分别是3、5、2、3,则正方形E的边长是 .
15. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的面积分别是3、5、2、3,则正方形E的边长是 . 16. 如图,在中, , , 分别以的三边为边向外作三个正方形 , , , 连接.过点作的垂线 , 垂足为 , 分别交 , 于点 , .若 , , 则四边形的面积是.
16. 如图,在中, , , 分别以的三边为边向外作三个正方形 , , , 连接.过点作的垂线 , 垂足为 , 分别交 , 于点 , .若 , , 则四边形的面积是.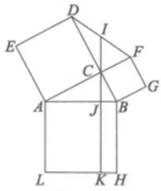
三、解答题
-
17. 计算:(1)、;(2)、 .18. 如图所示,在四边形中, , 且 .
 (1)、求的度数;(2)、若 , 求的值.19. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)、求的度数;(2)、若 , 求的值.19. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,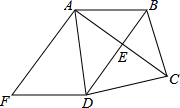 (1)、证明ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.20. 如图,将两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是否为菱形?请说明理由.
(1)、证明ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.20. 如图,将两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是否为菱形?请说明理由. 21. 小明在解决问题:已知a= ,求2a2﹣8a+1的值,他是这样分析与解答的:
21. 小明在解决问题:已知a= ,求2a2﹣8a+1的值,他是这样分析与解答的:∵a= .
∴a﹣2=﹣ .
∴(a﹣2)2=3,即a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)、计算: =;(2)、计算: +…+ ;(3)、若a= ,求2a2﹣8a+1的值.22. 如图1,在四边形中,和相交于点O,.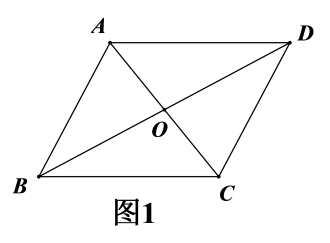
 (1)、求证:四边形是平行四边形;(2)、如图2,E,F,G分别是的中点,连接 , 若 , 求的周长.23. 如图1,为线段上一动点,分别过点B、D作 , , 连接、 . 已知 , , , 设 .
(1)、求证:四边形是平行四边形;(2)、如图2,E,F,G分别是的中点,连接 , 若 , 求的周长.23. 如图1,为线段上一动点,分别过点B、D作 , , 连接、 . 已知 , , , 设 . (1)、用含的代数式表示的长为;(2)、求的最小值;(3)、根据(2)中的规律和结论,请模仿图1在网格中(图2)构图并求代数式的最小值.
(1)、用含的代数式表示的长为;(2)、求的最小值;(3)、根据(2)中的规律和结论,请模仿图1在网格中(图2)构图并求代数式的最小值.

