广东省广州市白云区六校联考2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 如果二次根式有意义,那么x的取值范围是( )A、 B、 C、 D、2. 下列二次根式中与是同类二次根式的是( )A、 B、 C、 D、3. 下列运算,结果正确的是( )A、 B、 C、 D、4. 以下列各组数为边长,能组成直角三角形的是( )A、4,5,3 B、 , 2, C、2,2,2 D、1,2,25. 如图,在中, , D为边的中点, , 则长为( )
 A、2 B、3 C、4 D、66. 某游客为爬上千米高的山顶看日出,先用小时爬了千米休息小时后,用小时爬上山顶.游客爬山所用时间与山高间的函数关系用图形表示是( )A、
A、2 B、3 C、4 D、66. 某游客为爬上千米高的山顶看日出,先用小时爬了千米休息小时后,用小时爬上山顶.游客爬山所用时间与山高间的函数关系用图形表示是( )A、 B、
B、 C、
C、 D、
D、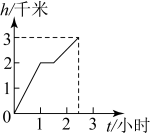 7. 顺次连接一个平行四边形的各边中点所得四边形的形状是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,平行四边形中,对角线、交于点E, , , , 则这个平行四边形面积为( )
7. 顺次连接一个平行四边形的各边中点所得四边形的形状是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,平行四边形中,对角线、交于点E, , , , 则这个平行四边形面积为( ) A、24 B、40 C、20 D、129. 如图,将边长分别是4,8的矩形纸片折叠,使点C与点A重合,则的长是( )
A、24 B、40 C、20 D、129. 如图,将边长分别是4,8的矩形纸片折叠,使点C与点A重合,则的长是( )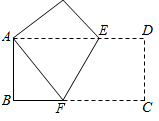 A、2 B、3 C、 D、410. 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )
A、2 B、3 C、 D、410. 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )①;②与EGD全等的三角形共有2个;③S四边形ODEG=S四边形ABOG;④由点A、B、D、E构成的四边形是菱形;
 A、①③④ B、①④ C、①②③ D、②③④
A、①③④ B、①④ C、①②③ D、②③④二、填空题
-
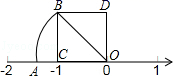
11. 计算: = .12. 如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 .
 13. 在△ABC中,D,E分别是边AB,AC的中点,若DE=2,则BC= .14. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则斜边AB= .
13. 在△ABC中,D,E分别是边AB,AC的中点,若DE=2,则BC= .14. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则斜边AB= .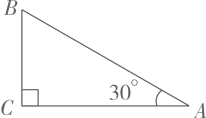 15. 如图,在矩形中,于E, , 则的度数为度.
15. 如图,在矩形中,于E, , 则的度数为度. 16. 如图,正方形ABCO和正方形DEFO的顶点A、E、O在同一直线l上,且 , , 给出下列结论:① , ② , ③△COF的面积 , ④ , 其中正确的是 .
16. 如图,正方形ABCO和正方形DEFO的顶点A、E、O在同一直线l上,且 , , 给出下列结论:① , ② , ③△COF的面积 , ④ , 其中正确的是 .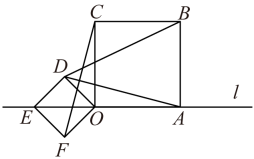
三、解答题
-
17.18. 在平面直角坐标系中画出函数的图象.在图象上标出横坐标为-4的点A,并写出它的坐标;
…
-3
-2
-1
0
1
2
3
…
…
…
19. 如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.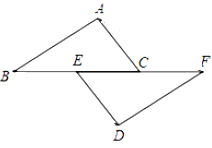 (1)、求证:△ABC≌△DFE;
(1)、求证:△ABC≌△DFE;
(2)、连接AF、BD,求证:四边形ABDF是平行四边形.20. 我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m. (1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?21. 如图,在四边形中, , , 点自点向以的速度运动,到点即停止.点自点向以的速度运动,点点即停止,点同时出发,设运动时间为 .
(1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?21. 如图,在四边形中, , , 点自点向以的速度运动,到点即停止.点自点向以的速度运动,点点即停止,点同时出发,设运动时间为 . (1)、当为何值时,四边形是平行四边形?(2)、当为何值时,四边形是平行四边形?22. 如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕.
(1)、当为何值时,四边形是平行四边形?(2)、当为何值时,四边形是平行四边形?22. 如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕. (1)、求CM的长;(2)、求梯形ABCE的面积.23. 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60˚的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
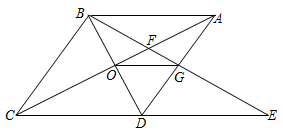
(1)、求CM的长;(2)、求梯形ABCE的面积.23. 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60˚的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.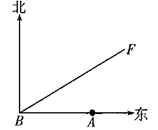 (1)、A城是否受到这次台风的影响?为什么?(2)、若A城受到这次台风影响,则A城遭受这次台风影响有多长时间?24. 如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)、A城是否受到这次台风的影响?为什么?(2)、若A城受到这次台风影响,则A城遭受这次台风影响有多长时间?24. 如图1,对角线互相垂直的四边形叫做垂美四边形.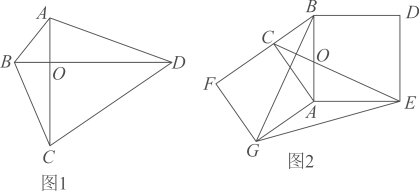 (1)、概念理解:给出下列图形:①平行四边形;②矩形;③菱形;④正方形.其中一定是“垂美四边形”的是(填序号);(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.求证:AB2+CD2=AD2+BC2;(3)、解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC= , AB=3
(1)、概念理解:给出下列图形:①平行四边形;②矩形;③菱形;④正方形.其中一定是“垂美四边形”的是(填序号);(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.求证:AB2+CD2=AD2+BC2;(3)、解决问题:如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC= , AB=3①请问四边形CGEB是垂美四边形吗?并说明理由;
②求GE的长.
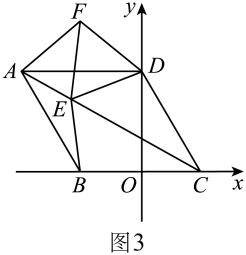
25. 如图1,四边形为菱形, , , , 且 . (1)、点B坐标为 , 点A坐标为 , 四边形的面积为;(2)、点E在线段上运动,为等边三角形.
(1)、点B坐标为 , 点A坐标为 , 四边形的面积为;(2)、点E在线段上运动,为等边三角形.①如图2,求证: , 并求的最小值;

②如图3,点E在线段上运动时,点F的横坐标是否发生变化?若不变,请求出点F的横坐标.若变化,请说明理由.