天津市河西区2022—2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 化简的结果为( )A、 B、 C、 D、2. 剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 由下列长度组成的各组线段中,能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列计算正确的是( )A、 B、 C、 D、5. 矩形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角相等 D、对角线互相垂直平分6. 若有点 , 点 , 则的长度为( )A、 B、 C、 D、7. 在平行四边形中, , 则的度数为( )
3. 由下列长度组成的各组线段中,能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列计算正确的是( )A、 B、 C、 D、5. 矩形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角相等 D、对角线互相垂直平分6. 若有点 , 点 , 则的长度为( )A、 B、 C、 D、7. 在平行四边形中, , 则的度数为( )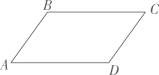 A、 B、 C、 D、8. 通过描点画图,画出了函数的图象如图所示,可以看到直线从左到右上升,即当自变量x由小变大时,函数y随x的增大而( )
A、 B、 C、 D、8. 通过描点画图,画出了函数的图象如图所示,可以看到直线从左到右上升,即当自变量x由小变大时,函数y随x的增大而( )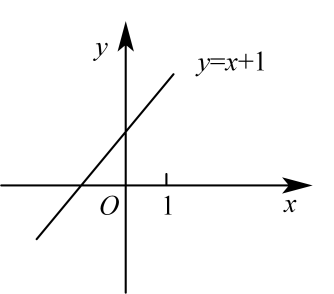 A、增大 B、减小 C、不变 D、有时增大有时减小9. 如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A、增大 B、减小 C、不变 D、有时增大有时减小9. 如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( ) A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间10. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )
A、-4和-3之间 B、3和4之间 C、-5和-4之间 D、4和5之间10. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )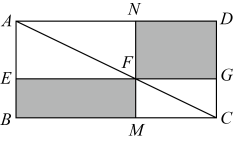 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 4的算术平方根是 .12. 边长为1的正方形的对角线长是 .13. 计算的结果为 .14. 如果实数x、y满足 , 则的平方根为 .15. 如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为.
 16. 如图,已知菱形的边长为 , , E为的中点,F为的中点,则的长等于 .
16. 如图,已知菱形的边长为 , , E为的中点,F为的中点,则的长等于 .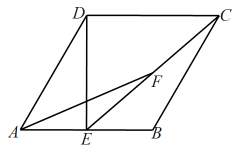
三、解答题
-
17. 计算:(1)、(2)、18. 已知 , , 求代数式的值.19. 如图,是一个正方形花园,公园内修建了两条小路和 , 且 , 那么这两条小路的长度相等吗?为什么?
 20. 已知:如图,在每个边长都为的小正方形网格中,点A,B,C都在格点上,连接 , , .
20. 已知:如图,在每个边长都为的小正方形网格中,点A,B,C都在格点上,连接 , , .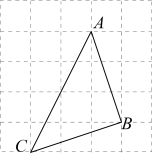 (1)、 的长为;的长为;(直接写出答案即可)(2)、 的周长为;(直接写出答案即可)(3)、请你利用图中的网格,在图中找到一个点D,并连接和 , 使得四边形是正方形.21. 如图,平行四边形中,点E,F分别在边 , 上, , . 连接 , .
(1)、 的长为;的长为;(直接写出答案即可)(2)、 的周长为;(直接写出答案即可)(3)、请你利用图中的网格,在图中找到一个点D,并连接和 , 使得四边形是正方形.21. 如图,平行四边形中,点E,F分别在边 , 上, , . 连接 , .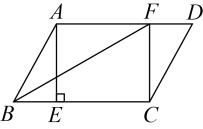 (1)、求证:四边形是矩形;(2)、若 , , 平分 , 求的长.22. 在“看图说故事”活动中,某学习小组结合图象(如下图)设计了一个问题情境.
(1)、求证:四边形是矩形;(2)、若 , , 平分 , 求的长.22. 在“看图说故事”活动中,某学习小组结合图象(如下图)设计了一个问题情境.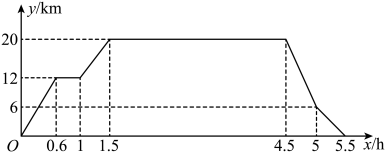
已知学校、书店、博物馆依次在同一条直线上,李华从学校出发,先骑行到书店,在书店停留了小时;然后去博物馆,在博物馆参观了3小时后回学校.给出的图象反映了这个过程中李华高学校的距离与离开学校的时间之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填空:①学校离书店的距离为;书店到博物馆的距离为;
②李华从博物馆骑行回学校用的时间为;
③李华从学校到书店骑行的平均速度为;
(2)、李华从博物馆回学校途中,是先快后慢,还是先慢后快?为什么?23. 将一个矩形纸片OABC放置在平面直角坐标系中,点O(0,0),点A(3,0),点C(0,6),点P在矩形的边OC上,折叠该纸片,使折痕所在的直线经过点P , 并与x轴的正半轴相交于点Q , 且 , 点O的对应点落在第一象限.设 .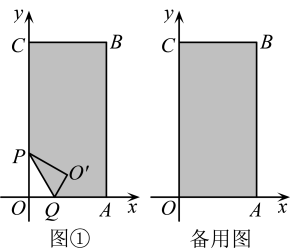 (1)、如图①,当时,求的大小和点的坐标;(2)、当点恰好落在AB边上时,求重合部分的面积.
(1)、如图①,当时,求的大小和点的坐标;(2)、当点恰好落在AB边上时,求重合部分的面积.