山西省晋中市平遥县2022-2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
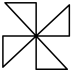 B、
B、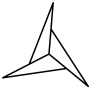 C、
C、 D、
D、 2. 公元前500年,古希腊毕达哥拉斯(Pythagoras)学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实:边长为1的正方形的对角线的长度是不可公度的,即不能表示成两个整数之比.这个发现是基于一个表述直角三角形三条边长之间关系的定理,请问这个定理被称为( )A、勾股定理 B、韦达定理 C、费马大定理 D、阿基米德折弦定理3. 关于x的一元一次不等式组的解集如图所示,则它的解集是( )
2. 公元前500年,古希腊毕达哥拉斯(Pythagoras)学派的弟子希帕索斯(Hippasus)发现了一个惊人的事实:边长为1的正方形的对角线的长度是不可公度的,即不能表示成两个整数之比.这个发现是基于一个表述直角三角形三条边长之间关系的定理,请问这个定理被称为( )A、勾股定理 B、韦达定理 C、费马大定理 D、阿基米德折弦定理3. 关于x的一元一次不等式组的解集如图所示,则它的解集是( ) A、 B、 C、 D、4. 如图,在平面内将绕着直角顶点C逆时针旋转得到 . 若 , , 则线段的长为( )
A、 B、 C、 D、4. 如图,在平面内将绕着直角顶点C逆时针旋转得到 . 若 , , 则线段的长为( ) A、5 B、6 C、7 D、85. 等腰三角形的周长为 , 其中一边长为 , 则其腰长为( )A、 B、或 C、 D、以上都不对6. 如图所示,A , B , C , D四人在公园玩跷跷板,根据图中的情况,这四人体重从小到大排列的顺序为( )
A、5 B、6 C、7 D、85. 等腰三角形的周长为 , 其中一边长为 , 则其腰长为( )A、 B、或 C、 D、以上都不对6. 如图所示,A , B , C , D四人在公园玩跷跷板,根据图中的情况,这四人体重从小到大排列的顺序为( ) A、 B、 C、 D、7. 在平面直角坐标系中,将点向右平移2个单位长度再向上平移3个单位长度后得到的点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 把一些书分给同学,设每个同学分x本.若____;若分给11个同学,则书有剩余.可列不等式8(x+6)>11x , 则横线的信息可以是( )A、分给8个同学,则剩余6本 B、分给6个同学,则剩余8本 C、如果分给8个同学,则每人可多分6本 D、如果分给6个同学,则每人可多分8本9. 如图,在中,平分 , , 垂足为点E . 若的面积为16, , 则的长为( )
A、 B、 C、 D、7. 在平面直角坐标系中,将点向右平移2个单位长度再向上平移3个单位长度后得到的点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 把一些书分给同学,设每个同学分x本.若____;若分给11个同学,则书有剩余.可列不等式8(x+6)>11x , 则横线的信息可以是( )A、分给8个同学,则剩余6本 B、分给6个同学,则剩余8本 C、如果分给8个同学,则每人可多分6本 D、如果分给6个同学,则每人可多分8本9. 如图,在中,平分 , , 垂足为点E . 若的面积为16, , 则的长为( ) A、2 B、3 C、4 D、610. 某企业次定购买A,B两种型号的污水处理设备共8台,具体情况如下表:
A、2 B、3 C、4 D、610. 某企业次定购买A,B两种型号的污水处理设备共8台,具体情况如下表:A型
B型
价格(万无台)
12
10
月污水处理能力(吨月)
200
160
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低1380吨,该企业有哪些购买方案呢?这解决这个问题,高购买A型污水处理设备x台,所列不等式组正确的是
A、 B、 C、 D、二、填空题
-
11. “x的5倍与y的差大于1”用不等式表示为.12. 如图,点A、B分别在x轴和y轴上, , , 若将线段平移至 , 则的值为 .
 13. 如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为.
13. 如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为. 14. 对于任意实数a、b , 定义一种运算:a※ . 例如,2※ . 请根据上述的定义解决问题:若不等式3※ , 则不等式的正整数解是__.15. 如图,的点在直线l上, , 若点P在直线l上运动,当成为等腰三角形时,则度数是 .
14. 对于任意实数a、b , 定义一种运算:a※ . 例如,2※ . 请根据上述的定义解决问题:若不等式3※ , 则不等式的正整数解是__.15. 如图,的点在直线l上, , 若点P在直线l上运动,当成为等腰三角形时,则度数是 .
三、解答题
-
16.(1)、解不等式: .(2)、解不等式组: , 并将解集在数轴上表示出来.17. 如图,方格纸中的每个小方格都是边长为个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点C的坐标 .
 (1)、把向上平移个单位后得到对应的 , 请你画出 .(2)、以点A为旋转中心,画出把逆时针旋转所得的 .(3)、以原点O为对称中心,画出关于原点O对称的 , 并写出点的坐标.18. 为建设“醉美泸州”,泸州市绿化改造工程正如火如荼进行,某施工队计划购买甲、乙两种树苗共400棵对蜀泸大道某路段进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元,若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?19. 在① , ② , ③请你在这三个条件中选择其中一个,补充在下面的问题中横线上,并完成问题的解答.
(1)、把向上平移个单位后得到对应的 , 请你画出 .(2)、以点A为旋转中心,画出把逆时针旋转所得的 .(3)、以原点O为对称中心,画出关于原点O对称的 , 并写出点的坐标.18. 为建设“醉美泸州”,泸州市绿化改造工程正如火如荼进行,某施工队计划购买甲、乙两种树苗共400棵对蜀泸大道某路段进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元,若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?19. 在① , ② , ③请你在这三个条件中选择其中一个,补充在下面的问题中横线上,并完成问题的解答.问题:如图,在中, , 点D在边上(不与点A,点B重合),点E在边上(不与点A,点C重合),连接 , , 与相交于点F.若 ,求证: .
 20. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点A在第二象限内作 , 且 .
20. 如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点A在第二象限内作 , 且 . (1)、如图,求线段的长度;(2)、如图,将向右平移得到 , 点A的对应点始终在x轴上,当点C的对应点正好落在直线上,求此时的坐标.
(1)、如图,求线段的长度;(2)、如图,将向右平移得到 , 点A的对应点始终在x轴上,当点C的对应点正好落在直线上,求此时的坐标. 21. 阅读下面解题过程,再解答后面的问题.
21. 阅读下面解题过程,再解答后面的问题.学习了一元一次不等式组的解法,老师给同学们布置了一个任务,请大家探究并求出不等式 的解集.
小丽类比有理数的乘法法则,根据“同号两数相乘,积为正”可以得到:①或② , 解不等式组①得 , 解不等式组②得 , 所以原不等式解集为或 . 请你仿照上述方法,求不等式的的解集.
22. 小宇遇到了这样一个问题:已知:如图, ,点A,B分别在射线OM,ON上,且满足 .
求作:线段OB上的一点C,使 的周长等于线段 的长.
以下是小宇分析和求解的过程,请补充完整:首先画草图进行分析,如图1所示,若符合题意得点C已经找到,即 得周长等于OB的长,那么由 ,可以得到 .
对于这个式子,可以考虑用截长得办法,在BC上取一点D,使得 ,那么就可以得到 .
若连接AD,由 . (填推理依据).可知点C在线段AD得垂直平分线上,于是问题得解法就找到了.
请根据小宇得分析,在图2中完成作图(尺规作图,不写做法,保留作图痕迹).
 23. 综合实践
23. 综合实践在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成的,在相对位置变化的同时,始终存在一对全等三角形.兴趣小组成员经过研讨给出定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,可以形象地看作两双手,所以通常称为“手拉手模型”.如图1,与都是等腰三角形,其中 , 则 .
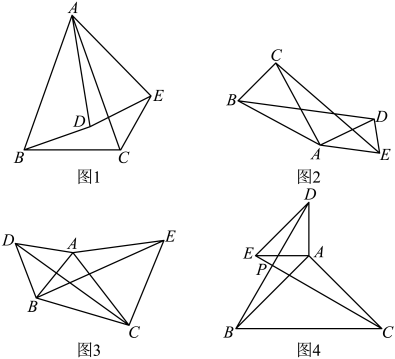 (1)、【初步把握】如图2,与都是等腰三角形, , , 且 , 则有 .(2)、【深入研究】如图3,已知 , 以为边分别向外作等边和等边 , 并连接BE , , 求证: .(3)、【拓展延伸】如图4,在两个等腰直角三角形和中, , , , 连接 , , 交于点P , 请判断和的关系,并说明理由.
(1)、【初步把握】如图2,与都是等腰三角形, , , 且 , 则有 .(2)、【深入研究】如图3,已知 , 以为边分别向外作等边和等边 , 并连接BE , , 求证: .(3)、【拓展延伸】如图4,在两个等腰直角三角形和中, , , , 连接 , , 交于点P , 请判断和的关系,并说明理由.