山西省晋中市2022-2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 若x是非负数,则用不等式可表示为( )A、 B、 C、 D、2. 下列汽车标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 以下列各组线段为边作三角形,不能作出直角三角形的是( )A、6,8,10 B、5,12,13 C、1,2, D、 , ,4. 不等式的解集在数轴上可表示为( )A、
3. 以下列各组线段为边作三角形,不能作出直角三角形的是( )A、6,8,10 B、5,12,13 C、1,2, D、 , ,4. 不等式的解集在数轴上可表示为( )A、 B、
B、 C、
C、 D、
D、 5. 如图,经过水平向右平移后得到 , 若 , , 则平移的距离为( )
5. 如图,经过水平向右平移后得到 , 若 , , 则平移的距离为( )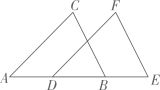 A、 B、 C、 D、6. 不等式组的最大整数解为( )A、3 B、2 C、0 D、-27. 如图,已知 , 与交于点O,添加一个适当的条件后,仍不能使得成立的是( )
A、 B、 C、 D、6. 不等式组的最大整数解为( )A、3 B、2 C、0 D、-27. 如图,已知 , 与交于点O,添加一个适当的条件后,仍不能使得成立的是( ) A、 B、 C、 D、8. 某校在一次外出郊游中,把学生编为9个组,若每组比预定的人数多人,则学生总数超过人;若每组比预定的人数少人,则学生总数不到人,那么每组预定的学生人数为( )A、21人 B、22人 C、23人 D、24人9. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 点恰好落在边上,且 , 则的度数为( )
A、 B、 C、 D、8. 某校在一次外出郊游中,把学生编为9个组,若每组比预定的人数多人,则学生总数超过人;若每组比预定的人数少人,则学生总数不到人,那么每组预定的学生人数为( )A、21人 B、22人 C、23人 D、24人9. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 点恰好落在边上,且 , 则的度数为( ) A、 B、 C、 D、10. 如图,的顶点 , , 点C在y轴的正半轴上, , 将向右平移得到 , 若直线经过点C,则点的坐标为( )
A、 B、 C、 D、10. 如图,的顶点 , , 点C在y轴的正半轴上, , 将向右平移得到 , 若直线经过点C,则点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 命题“如果 , 那么”的逆命题是命题(填“真”或“假”).12. 若点A(a,3)与点B(﹣4,b)关于原点对称,则a﹣b= .13. 如图,射线是的平分线,C是射线上一点,于点F . 若D是射线上一点,且 , 则的面积是 .
 14. 若不等式组无解,则a的取值范围是 .15. 如图,在中,D为边上一点,且平分 , 过A作于点若 , , , , 则 .
14. 若不等式组无解,则a的取值范围是 .15. 如图,在中,D为边上一点,且平分 , 过A作于点若 , , , , 则 .
三、解答题
-
16.(1)、解不等式:;(2)、解不等式组: .17. 如图,在中, .
 (1)、请用直尺和圆规作边上的垂直平分线 , 交于点D,交于点E.(要求:不写作法,标明字母并保留作图痕迹)(2)、在(1)中所作图的基础上,连接 , 若 , , 求的长.18. 如图,一次函数的图象与轴交于点B,与正比例函数的图象交于点 .
(1)、请用直尺和圆规作边上的垂直平分线 , 交于点D,交于点E.(要求:不写作法,标明字母并保留作图痕迹)(2)、在(1)中所作图的基础上,连接 , 若 , , 求的长.18. 如图,一次函数的图象与轴交于点B,与正比例函数的图象交于点 . (1)、求的面积;(2)、利用函数图象直接写出当时,x的取值范围.19. 如图,在平面直角坐标系中,的顶点C的坐标为 .
(1)、求的面积;(2)、利用函数图象直接写出当时,x的取值范围.19. 如图,在平面直角坐标系中,的顶点C的坐标为 . (1)、画出 , 使得与关于原点O对称,并写出的坐标;(2)、以O为旋转中心,将逆时针旋转得到 , 画出并写出的坐标.20. 阅读与思考
(1)、画出 , 使得与关于原点O对称,并写出的坐标;(2)、以O为旋转中心,将逆时针旋转得到 , 画出并写出的坐标.20. 阅读与思考请阅读下列材料,并完成相应的任务,
两点间的距离公式:如果平面直角坐标系内有两点 , , 那么两点间的距离 , 例如:若点 , , 则 .
(1)、已知 , , 求A,B两点间的距离;(2)、已知 , , , 判断的形状.21. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?22. 综合与实践问题情境:在综合实践课上,同学们探究“全等的等腰直角三角形图形变化问题”.
如图1,已知 , 点C与点E重合,其中 , .
 (1)、将图1中的两个全等的和按如图2所示方式摆放,点B落在上,所在直线交所在直线于点M,连接 , 求证; .(2)、将图1中的绕点A按逆时针方向旋转(如图),然后分别延长 , , 它们相交于点F,连接 . 求证:为等边三角形.(3)、将图1中的绕点A按顺时针方向旋转(如图),线段和相交于点F,连接 , 求线段的长.23. 综合与探究
(1)、将图1中的两个全等的和按如图2所示方式摆放,点B落在上,所在直线交所在直线于点M,连接 , 求证; .(2)、将图1中的绕点A按逆时针方向旋转(如图),然后分别延长 , , 它们相交于点F,连接 . 求证:为等边三角形.(3)、将图1中的绕点A按顺时针方向旋转(如图),线段和相交于点F,连接 , 求线段的长.23. 综合与探究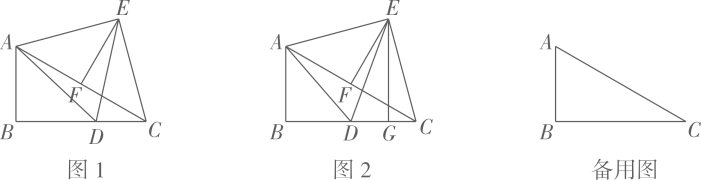
如图1,在中, , , , D为边上一动点,以为边在其右侧作等边三角形 , F为的中点,连接 , .
(1)、求证:;(2)、如图2,当D为的中点时,过点E作于点G,求的面积;(3)、若点D从点B处运动到点C处,直接写出点E所经过的路径长.