山西省大同市灵丘县2022―2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 若代数式有意义,则实数x的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 下列运算中正确的是( )A、 B、 C、 D、4. 以下列长度作为三边构建三角形,能构成直角三角形的是( )A、2,3,4 B、 , , 5 C、2,2, D、1,2,5. 下列命题的逆命题是假命题的是( )A、平行四边形的对角线互相平分 B、矩形的两条对角线相等 C、两直线平行,内错角相等 D、菱形的四条边都相等6. 如图,在中,D、E分别是、边的中点,已知的周长为18,则的周长为( )
 A、6 B、8 C、9 D、127. 如图,位于第一象限中,已知顶点A、C的坐标分别为 , , 则顶点B的坐标为( )
A、6 B、8 C、9 D、127. 如图,位于第一象限中,已知顶点A、C的坐标分别为 , , 则顶点B的坐标为( )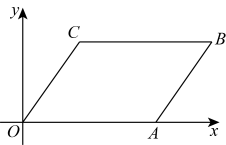 A、 B、 C、 D、8. 正方形的对角线长为 , 则其周长为( )A、8 B、 C、 D、169. 如图,在菱形中, , 对角线 , 则菱形的面积是( )
A、 B、 C、 D、8. 正方形的对角线长为 , 则其周长为( )A、8 B、 C、 D、169. 如图,在菱形中, , 对角线 , 则菱形的面积是( ) A、 B、 C、 D、10. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )
A、 B、 C、 D、10. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )①;②;③;④;⑤
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
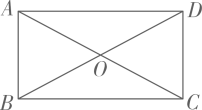
11. 已知a,b,c是三角形三边长,则化简.12. 在平面直角坐标系中,点到原点的距离是 .13. 如图,已知ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使ABCD成为一个矩形.你添加的条件是 .
 14. 如图,将一个平行四边形木框变形为矩形 , 其面积增加了一倍,则原平行四边形中最小的内角度数是 .
14. 如图,将一个平行四边形木框变形为矩形 , 其面积增加了一倍,则原平行四边形中最小的内角度数是 . 15. 如图,正方形边长为 , 点E为边中点,沿直线折叠,点C落在点F处,延长交于点G,连接 , 则的面积为 .
15. 如图,正方形边长为 , 点E为边中点,沿直线折叠,点C落在点F处,延长交于点G,连接 , 则的面积为 .
三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 如图,中,平分 , 平分 , 求证:四边形是平行四边形.
 18. 黄金分割比例是使矩形最具美感的比例,即矩形的宽与长之比为 , 这样的矩形被称为黄金矩形,如古希腊的帕特农神庙其立面就接近于黄金矩形,小华想设计一张版面为黄金矩形的海报,已知海报的宽为 , 则海报的长应设计为多少?19. 如图,正方形网格图中,每个小正方形的边长都是1.
18. 黄金分割比例是使矩形最具美感的比例,即矩形的宽与长之比为 , 这样的矩形被称为黄金矩形,如古希腊的帕特农神庙其立面就接近于黄金矩形,小华想设计一张版面为黄金矩形的海报,已知海报的宽为 , 则海报的长应设计为多少?19. 如图,正方形网格图中,每个小正方形的边长都是1. (1)、在图中分别画出线段 , , ;(2)、判断以 , , 三条线段为边能否构成直角三角形,并说明理由.20. 如图,正方形中,点E为对角线上的一点, , , 垂足分别为F,G,已知 , , 求的长度.
(1)、在图中分别画出线段 , , ;(2)、判断以 , , 三条线段为边能否构成直角三角形,并说明理由.20. 如图,正方形中,点E为对角线上的一点, , , 垂足分别为F,G,已知 , , 求的长度. 21. 在进行二次根式的化简时,我们有时会遇到形如的式子,对于这类式子我们可以进一步将其化简,使其分母转化为有理数,这一过程叫做分母有理化.
21. 在进行二次根式的化简时,我们有时会遇到形如的式子,对于这类式子我们可以进一步将其化简,使其分母转化为有理数,这一过程叫做分母有理化.例如:
(1)、用上述方法化简;(2)、计算: .22. 综合与实跷通过对《平行四边形》一章内容的学习,我们可以认识到矩形、菱形都是特殊的平行四边形,它们除了具有平行四边形的性质外,还有各自的特殐性质,联系前面学过的三角形知识,我们会发现矩形和菱形中能得到很多特殊的三角形,因此在解决矩形、菱形问题时经常会用到特殊三角形的知识.请你运用所学的知识解答下面的题目.
如图所示,在中, , D、E两点分别为、两边的中点,过点C作的平行线,与的延长线相交于点F,连接 .
 (1)、求证:四边形是菱形;(2)、当满足什么条件时,四边形是正方形?请说明理由.23. 综合与探究
(1)、求证:四边形是菱形;(2)、当满足什么条件时,四边形是正方形?请说明理由.23. 综合与探究折纸是一种艺术,其中也包含了高超的技术,数学折纸活动有益于开发智力,拓展思维,在折纸活动中体会数学知识的内涵,理解数学知识的应用,可以让我们感悟到严谨的数学之美,八(4)班数学兴趣小组的同学们在活动课进行了折纸问题探究.

【方法提示】
数学折纸问题的解决通常结合轴对称和全等的相关知识性质,要关注折叠前后对应的边和对应的角等一些不变的关系.
【动手操作】
如图,将一张矩形纸片沿长边进行折叠(已知),使点C落在边上,折痕为(点E在边上,点F在边上),折叠后点C,D的对应点分别为点G,H.
【问题探究】
(1)、判断图中四边形的形状,并证明你的结论.(2)、随着点C落在不同的位置,折痕位置也在变化,若矩形纸片中 , , 求线段长度的取值范围.