山西省大同市2022-2023学年八年级下学期数学期中教学质量监测试卷

试卷更新日期：2023-05-29 类型：期中考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥1 B、x＞1 C、x＜1 D、x≤1

查看试题解析
2. 如图，菱形 $A B C D$ 中，若 $∠ C = 100 °$ ，则 $∠ A B D$ 的度数是（）

A、 $10 °$ B、 $40 °$ C、 $50 °$ D、 $80 °$

查看试题解析
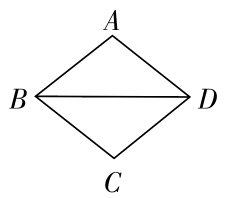3. 下列长度的三条线段中，能组成等腰直角三角形的是（）

A、1，2，2 B、 $\sqrt{2}$ ， $\sqrt{2}$ ， 1 C、3，4，5 D、 $\sqrt{3}$ ， $\sqrt{3}$ ， $\sqrt{6}$

查看试题解析
4. 图1是三角形空地，计划用栅栏分成两部分种植不同的植物如图2，则栅栏AB的长度是（）

A、2m B、3m C、4m D、1m

查看试题解析
5. 下列计算正确的是（）

A、 ${(3 \sqrt{3})}^{2} = 3 \times 3 = 9$ B、 $\sqrt{{(- \frac{2}{5})}^{2}} = \frac{2}{5}$ C、 $\sqrt{9 + 16} = \sqrt{9} + \sqrt{16}$ D、 $\sqrt{(- 9) \times (- 16)} = \sqrt{- 9} \times \sqrt{- 16}$

查看试题解析
6. 化简二次根式除了利用二次根式的运算法则外，还可以借助图形解译和验证．如化简 $\sqrt{8}$ ，我们可以构造如图所示的图形，其中图1是一个面积为8的正方形，图2是一个面积为2的正方形，根据两图的关系我们可以得到 $\sqrt{8} = 2 \sqrt{2}$ ．这种分析问题的方法所体现的数学思想是（）

A、分类讨论思想 B、从一般到特殊思想 C、数形结合思想 D、类比思想

查看试题解析
7. 如图所示，在四边形 $A B C D$ 中，已知 $∠ 1 = ∠ 2$ ，添加下列一个条件，不能判断四边形 $A B C D$ 成为平行四边形的是（　　）

A、 $∠ D = ∠ B$ B、 $A B ∥ C D$ C、 $A D = B C$ D、 $A B = D C$

查看试题解析
8. 毕达哥拉斯树也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树状图形，其中所有的四边形都是正方形，所有的三角形都是直角三角形．如图，若正方形A，B，C，D的边长分别是2，3，1，2，则正方形G的边长是（）

A、8 B、 $2 \sqrt{2}$ C、 $3 \sqrt{2}$ D、5

查看试题解析
9. 如图，△ABC是边长为2的等边三角形，将△ABC沿射线BC向右平移到△DCE ，连接AD ， BD ，下列结论错误的是（）

A、AD＝BC B、BD⊥DE C、四边形ACED是菱形 D、四边形ABCD的面积为4 $\sqrt{3}$

查看试题解析
10. 如图，在墙角处放着一个长方体木柜（木柜与墙面和地面均没有缝腺），一只蚂蚁从柜角 $A$ 处沿着木柜表面爬到柜角 $C_{1}$ 处．若 $A B = 3$ ， $B C = 4$ ， $C C_{1} = 5$ ，则蚂蚁爬行的最短路程是（）

A、 $\sqrt{74}$ B、 $3 \sqrt{10}$ C、 $\sqrt{89}$ D、12

查看试题解析

二、填空题

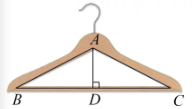
11. 将二次根式 $\sqrt{48}$ 化为最简二次根式的结果是

查看试题解析
12. 计算 $4 \sqrt{2} (\sqrt{2} + 1)$ 的结果是．

查看试题解析
13. 如图所示的衣架可以近似看成一个等腰三角形ABC，其中 $A B = A C = 25 c m$ ，底边BC的长 $48 c m$ ，那么衣架的高 $A D =$ $c m$ .

查看试题解析
14. 如图，平行四边形 $A B C D$ 的周长是 $18 c m$ ， $A C$ ， $B D$ 相交于点 $O$ ， $O E ⊥ B D$ 交 $A D$ 于点 $E$ ，则 $△ A B E$ 的周长是 $c m$ ．

查看试题解析
15. 如图，点G是正方形 $A B C D$ 对角线 $C A$ 的延长线上任意一点，以线段 $A G$ 为边作一个正方形 $A E F G$ ，线段 $E B$ ， $G D$ 相交于点H ，若 $A B = 2 ， A G = \sqrt{2}$ ，则 $E B$ ＝__．

查看试题解析

三、解答题

16. 计算

(1)、 $\sqrt{\frac{1}{6}} \times \sqrt{96} \div \sqrt{6}$ ；

(2)、 $\sqrt{80} - \sqrt{8} - \sqrt{45} + 4 \sqrt{\frac{1}{2}}$ ．

查看试题解析
17. 已知 $x = 2 + \sqrt{3}$ ， $y = 2 - \sqrt{3}$ ，求下列各式的值：

(1)、 $\frac{1}{x} + \frac{1}{y}$

(2)、 $x^{2} + y^{2}$ ．

查看试题解析
18. 如图，在正方形网格中，每个小正方形的边长均为1，小正方形的顶点叫做格点．

(1)、在图1中，以格点为端点，画线段 $M N = \sqrt{29}$ ；

(2)、在图2中，以格点为顶点，画正方形 $A B C D$ ，使它的面积为10

查看试题解析
19. 有一块矩形木块，木工采用如图方式，求木板上截出两个面积分别为18dm²和32dm²的正方形木板，求剩余木料的面积．

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A B = 6 cm$ ， $B C = 10 cm$ ， $∠ B =60 °$ ，点G是 $C D$ 的中点．点E是 $A D$ 边上的动点，连接 $E G$ 并延长交 $B C$ 的延长线交于点F，连接 $C E$ ， $D F$ ．

(1)、求证：四边形 $C E D F$ 是平行四边形．

(2)、当 $A E =$ $cm$ 时，四边形 $C E D F$ 是菱形．

查看试题解析
21. 某校为迎接六十周年校庆，准备将一块三角形空地 $A B C$ 进行规划．如图，点D是 $B C$ 边上的一点．经测量， $A B = 26 m$ ， $A D = 24 m$ ， $B D = 10 m$ ， $A C$ 比 $C D$ 长 $12 m$ ．

(1)、求 $△ A B D$ 的面积；

(2)、求 $A C$ 的长．

查看试题解析
22. 阅读下面材料，并完成相应的任务．
三等分角是古希腊三大几何问题之一．如图，任意 $∠ A B C$ 可被看作是矩形 $A C B D$ 的对角线 $B A$ 与边 $B C$ 的夹角，以点B为端点的射线 $B F$ 交 $A C$ 于点E，交 $D A$ 的延长线于点F．若 $E F = 2 A B$ ，则 $∠ C B F$ 是 $∠ A B C$ 的一个三等分角．

证明：如图，取 $E F$ 的中点G，连接 $A G$ ．

∵四边形 $A C B D$ 是矩形，∴ $∠ D A C = 90 °$ ， $A D ∥ B C$ ． ∴ $∠ E A F = 180 ° - ∠ D A C = 90 °$ ．

在 $Rt △ A E F$ 中，∵点G是 $E F$ 的中点，∴ $A G = \frac{1}{2} E F$ ， $F G = \frac{1}{2} E F$ ， $A G = F G$ ．

……

(1)、任务一：上而证明过程中得出“ $A G = \frac{1}{2} E F$ ”的依据是；

(2)、任务二：完成材料证明中的剩余部分．

查看试题解析
23. 如图，在矩形 $A B C D$ 中， $A D = 6$ ， $A B = 8$ ．

(1)、如图1，点E，F分别在边 $A B$ ， $C D$ 上，分别沿 $D E$ ， $B F$ 折叠 $△ D A E$ 和 $△ B C F$ ，点A的对应点G与点C的对应点H均落在对角线 $B D$ 上．
①试判断四边形 $B E D F$ 的形状，并说明理由；

②求 $H G$ 的长．

(2)、如图2，点P是 $C D$ 上一点，连接 $P A$ ，点E，F分别在边 $A D$ ， $A B$ 上，分别沿 $P E$ ， $P F$ 折叠 $△ P D E$ 和四边形 $P C B F$ ，点B的对应点是点 $B^{'}$ ，点D的对应点 $D^{'}$ 与点 $C$ 的对应点 $C^{'}$ 均落在 $P A$ 上，连接 $D^{'} F$ ，且点E， $D^{'}$ ， $F$ 三点在同一条直线上．
①判断四边形 $B^{'} C^{'} D^{'} F$ 的形状，并说明理由；

②直接写出四边形 $B^{'} C^{'} D^{'} F$ 的面积

查看试题解析