山东省枣庄市峄城区2022-2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列与2022年冬奥会相关的图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知a,b,c,d是实数,若 , , 则( )A、 B、 C、 D、3. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、4. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
2. 已知a,b,c,d是实数,若 , , 则( )A、 B、 C、 D、3. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、4. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、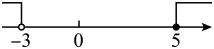 B、
B、 C、
C、 D、
D、 5. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
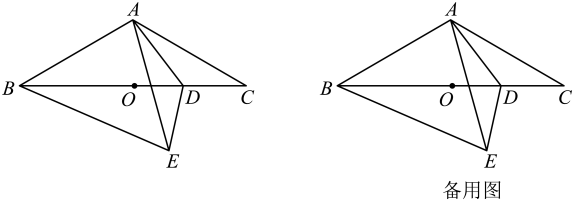
5. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )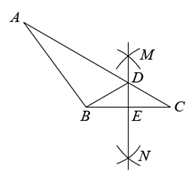 A、25 B、22 C、19 D、186. 如图,已知在锐角△ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连结EB,EC.若∠EBC=45°,BC=6,则△EBC的面积是( )
A、25 B、22 C、19 D、186. 如图,已知在锐角△ABC中,AB=AC,AD是△ABC的角平分线,E是AD上一点,连结EB,EC.若∠EBC=45°,BC=6,则△EBC的面积是( ) A、12 B、9 C、6 D、7. 如图,在中,的平分线交于点D , DE//AB , 交于点E , 于点F , , 则下列结论错误的是( )
A、12 B、9 C、6 D、7. 如图,在中,的平分线交于点D , DE//AB , 交于点E , 于点F , , 则下列结论错误的是( ) A、 B、 C、 D、8. 如图,边长为1的正方形网格图中,点 , 都在格点上,若 , 则的长为( )
A、 B、 C、 D、8. 如图,边长为1的正方形网格图中,点 , 都在格点上,若 , 则的长为( )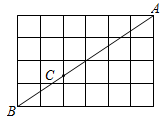 A、 B、 C、 D、9. 如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( )
A、 B、 C、 D、9. 如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( ) A、2cm B、3cm C、4cm D、5cm10. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( )
A、2cm B、3cm C、4cm D、5cm10. 活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如已知△ABC中,∠A=30°, AC=3,∠A所对的边为 , 满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为( ) A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题
-
11. 某品牌护眼灯的进价为240元,商店以320元的价格出售.“五一节”期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该护眼灯最多可降价元.
 12. 关于x的不等式组 恰有3个整数解,则a的取值范围是.13. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.
12. 关于x的不等式组 恰有3个整数解,则a的取值范围是.13. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.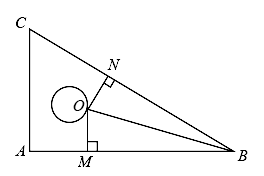 14. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.
14. 如图.在 中, , .以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于 长为半径作弧,在 内两弧相交于点P;作射线AP交BC于点F,过点F作 ,垂足用G.若 ,则 的周长等于cm.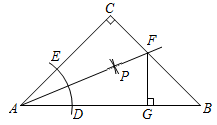 15. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.
15. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.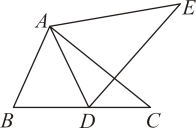 16. 如图,在中, . 把沿方向平移 , 得到 , 连结 , 则四边形的周长为 .
16. 如图,在中, . 把沿方向平移 , 得到 , 连结 , 则四边形的周长为 .
三、解答题
-
17. 解不等式 ,并在数轴上表示解集.
 18. 解不等式组 . 请结合题意完成本题的解答(每空只需填出最后结果).
18. 解不等式组 . 请结合题意完成本题的解答(每空只需填出最后结果).解:
( 1 )解不等式①,得_▲_ .
( 2 )解不等式②,得_▲_ .
( 3 )把不等式①和②的解集在数轴上表示出来.

( 4 )所以原不等式组解集为_▲_ .
19. 如图,△ 是等边三角形, 在直线 上, .

求证: .
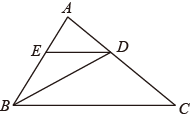
20. 如图,在的方格纸中,已知格点P , 请按要求画格点图形(顶点均在格点上). (1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转后的图形.21. 如图, BD 是 △ABC的角平分线, DE∥BC ,交 AB 于点E.
(1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转后的图形.21. 如图, BD 是 △ABC的角平分线, DE∥BC ,交 AB 于点E.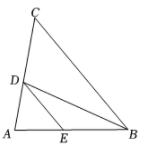 (1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.22. 某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元.(1)、求篮球和足球的单价分别是多少元;(2)、学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么有哪几种购买方案?
(1)、求证: .(2)、当AB=AC时,请判断 CD 与ED的大小关系,并说明理由.22. 某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元.(1)、求篮球和足球的单价分别是多少元;(2)、学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么有哪几种购买方案?