山东省青岛市城阳区2022-2023学年八年级下学期数学期中试卷

试卷更新日期：2023-05-29 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $a > b$ ，则下列不等式成立的是（）

A、 $a - 2 < b - 2$ B、 $2 a > 2 b$ C、 $- 2 a > - 2 b$ D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
2. 不等式 $2 x - 1 < 3$ 的正整数解是（）

A、 $x < 2$ B、 $x > 2$ C、 $1$ D、 $2$

查看试题解析
3. 下列四个图形中，能通过基本图形平移得到的有（）个图形

A、 $4$ B、 $3$ C、 $2$ D、 $1$

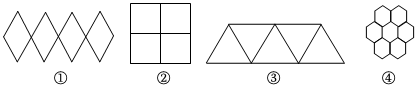查看试题解析
4. 到三角形三条边的距离都相等的点是这个三角形的（　　）

A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点

查看试题解析
5. 不等式的解在数轴上如图所示，则这个不等式的解是（　　）

A、 $x > - 1$ B、 $x \geq - 1$ C、 $x < - 1$ D、 $x \leq - 1$

查看试题解析
6. 下列不等式组中，解集是2＜x＜3的不等式组是( 　)

A、 $\{\begin{matrix} x > 3 \\ x > 2 \end{matrix}$ B、 $\{\begin{matrix} x > 3 \\ x < 2 \end{matrix}$ C、 $\{\begin{matrix} x < 3 \\ x > 2 \end{matrix}$ D、 $\{\begin{matrix} x < 3 \\ x < 2 \end{matrix}$

查看试题解析
7. 下列说法中错误的是（）

A、中心对称图形的对称中心只有 $1$ 个，而轴对称图形的对称轴可能不止一条 B、等边三角形是轴对称图形，不是中心对称图形 C、图形在平移过程中，图形上的每一点都移动了相同的距离 D、图形在旋转过程中，图形上的每一点都绕旋转中心转过了同样长的路程

查看试题解析
8. 如图， $△ A D E$ 是由 $△ A B C$ 绕A点旋转得到的，若 $∠ C = 45 ° ， ∠ B = 90 ° ， ∠ C A D = 8 °$ ，则旋转角的度数为（）

A、 $98 °$ B、 $60 °$ C、 $53 °$ D、 $45 °$

查看试题解析

二、填空题

9. 不等式 $1 - 3 x < 13$ 的解集是．

查看试题解析
10. 等腰三角形的顶角为70°，则一腰上的高与底边所成的角的度数是度．

查看试题解析
11. 已知关于x的不等式 $x - a \geq - 3$ 的解集在数轴上表示如图，则a的值为．

查看试题解析
12. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 ° ， ∠ B = 30 ° ， C D ⊥ A B$ 于D ，若 $A B = 16 cm$ ，则 $A D =$ $cm$ ．

查看试题解析
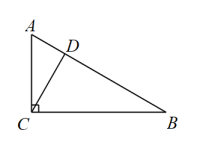13. 已知一次函数 $y = a x + b$ (a、b是常数，且 $a \neq 0$ )在平面直角坐标系中的图象如图所示，那么不等式 $a x + b < 2$ 的解集为．

查看试题解析
14. 某文艺团体为“希望工程”募捐组织了一场义演，共有 $50$ 元和 $70$ 元两种门票，某公司需购买 $100$ 张门票，且票价为 $70$ 元的票数不少于票价为 $50$ 元的票数的两倍，则购买这些门票最少需要元．

查看试题解析
15. 如图， $△ A B C$ 中， $C D$ 平分 $∠ A C B$ ， $B E ⊥ C D$ ， $∠ A = ∠ A B E$ ，若 $B D = 5$ ， $B C = 15$ ，则 $A C$ 的长为．

查看试题解析
16. 已知在同一平面直角坐标系中，一次函数 $y = \frac{2}{3} x + \frac{5}{6}$ 与 $y = - \frac{1}{2} x + 2$ 的图像如图所示，那么不等式 $\frac{2}{3} x + \frac{5}{6} > - \frac{1}{2} x + 2$ 的解集为．

查看试题解析

三、解答题

17. 用直尺、圆规作图，不写作法，但要保留作图痕迹．
已知： $△ A B C$ ；

求作：在 $△ A B C$ 内确定一点P ，使点P到顶点A、B距离相等，且到边 $A B$ 、 $A C$ 的距离也相等．

查看试题解析
18. 解不等式与不等式组：

(1)、解不等式 $\frac{3 - x}{2} > x + 3$ ，并把它的解集表示在数轴上．

(2)、求不等式组 ${\begin{array}{l} 2 x - 1 < 3 x + 1 \\ x + 2 < 5 \end{array}$ 的整数解．

(3)、解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$ ．

查看试题解析
19. 在平面直角坐标系中， $△ A B C$ 的位置如图所示，根据要求画出图形：

(1)、将 $△ A B C$ 向右平移6个单位，得到 $△ A_{1} B_{1} C_{1}$ ，画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A_{1} B_{1} C_{1}$ 绕点 $A_{1}$ 顺时针旋转 $90 °$ ，得到 $△ A_{2} B_{2} C_{2}$ ，画出旋转后的 $△ A_{2} B_{2} C_{2}$

查看试题解析
20. 春风四月暖，阅读正当时，某校今年4月开展“点燃读书激情，共建书香校园”活动，计划用3000元购买一批名著和辞典作为奖品，其中名著每套70元，辞典每本50元，现已购买名著24套，学校最多还能购买多少本辞典？

查看试题解析
21. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 90 °$ ， $B D$ 是 $△ A B C$ 的角平分线， $D E ⊥ B C$ 于点E， $E C = 4 cm$ ，求 $B C$ 的长度．

查看试题解析
22. 近年来，我国快递市场不断增长业务量，某快递公司为了提高快递分拣的速度，决定采购机器人来代替人工分拣，经市场调查发现，甲型机器人每台6万元，乙型机器人每台4万元，已知甲型和乙型机器人每台每小时分拣的快递件数分别为1200件和1000件，该公司计划采购这两种型号的机器人共8台，并且使这8台机器人每小时分拣的快递件数总和不少于8300件，则该公司至少需要投入多少万元才能完成采购计划？

查看试题解析
23. 如图，在等腰 $△ A B C$ 中，两条高线 $A D$ 和 $C E$ 交于点F， $A F = 2 C D$ ．

(1)、你能在图中找到一对全等三角形吗？请说明理由；

(2)、图中哪个三角形可以通过旋转得到另一个三角形？请说明是怎样旋转的．

查看试题解析
24. 某校组织学生“探寻红色印记，传承红色基因”为主题的研学旅行，全程导游讲解使学生增长见识，参加旅行的人数估计为30至50人(包含30人和50人)，甲、乙两家旅行社的服务质量相同，且报价都是每人1000元，经过协商，甲旅行社表示可给予每人八折优惠，且导游讲解免费；乙旅行社表示可给予每人七五折优惠，但需支付导游讲解费用共2000元，设该校有x人参加这次研学旅行，选择甲旅行社所需费用为 $y_{1}$ 元，选择乙旅行社所需费用为 $y_{2}$ 元．

(1)、求出 $y_{1}$ 与x之间的函数关系式， $y_{2}$ 与x之间的函数关系式．

(2)、若该校共有50人要参加此次旅游，则选择哪家旅行社可以使总费用较低？请说明理由．

(3)、计算说明人数在什么范围内，选乙旅行社合算．

查看试题解析