山东省济宁市任城区2022-2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 正方形具有而菱形不一定具有的性质是( )A、四条边都相等 B、对角线互相垂直且平分 C、对角线平分一组对角 D、对角线相等3. 一元二次方程 的根是( )
A、 B、 C、 , D、 ,4. 代数式有意义,则的取值范围是( )A、 B、 C、且 D、且5. 如图,矩形的对角线相交于点O , , 已知 , 则四边形的周长为( ) A、 B、 C、 D、6. 下列各式计算正确的是( )A、 B、 C、 D、7. 用配方法解方程x2+8x+7=0,则配方正确的是( )
A、 B、 C、 D、6. 下列各式计算正确的是( )A、 B、 C、 D、7. 用配方法解方程x2+8x+7=0,则配方正确的是( )
A、(x+4)2=9 B、(x-4)2=9 C、(x-8)2=16 D、(x+8)2=578. 若是一元二次方程,则m的值为( )A、2 B、 C、 D、9. 如图,在矩形中无重叠放入面积分别为16cm2和12 cm2的两张正方形纸片,则图中空白部分的面积为( ) A、 B、 C、 D、10. 如图,已知正方形ABCD边长是6,点P是线段BC上一动点,过点D作DE⊥AP于点E . 连接EC , 若 , 则△CDE的面积是( )
A、 B、 C、 D、10. 如图,已知正方形ABCD边长是6,点P是线段BC上一动点,过点D作DE⊥AP于点E . 连接EC , 若 , 则△CDE的面积是( ) A、18 B、 C、 D、14.4
A、18 B、 C、 D、14.4二、填空题
-
11. 若关于x的一元二次方程的一个根是 , 则k等于 .12. 写出一个与是同类二次根式的最简二次根式 . (不与原数相等)13. 在菱形ABCD中, , ,延长AB、CD,作矩形AECF,则矩形的边CE的长度是 .
 14. 若某等腰三角形的底和腰的长分别是一元二次方程的两根,则这个等腰三角形的周长是 .15. 如图,在菱形中, , , 是边的中点,P、M分别是 , 上的动点,连接、 , 则的最小值是 .
14. 若某等腰三角形的底和腰的长分别是一元二次方程的两根,则这个等腰三角形的周长是 .15. 如图,在菱形中, , , 是边的中点,P、M分别是 , 上的动点,连接、 , 则的最小值是 .
三、解答题
-
16. 计算: .17. 用配方法解 .18. 已知关于x的一元二次方程 .(1)、当时,请求出方程的解;(2)、试说明方程总有两个实数根.19. 已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.
 (1)、求证:四边形ACDE是平行四边形;(2)、若∠AFC=2∠B.求证:四边形ACDE是矩形.20. 某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,求增加了多少行?21. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)、求证:四边形ACDE是平行四边形;(2)、若∠AFC=2∠B.求证:四边形ACDE是矩形.20. 某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,求增加了多少行?21. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE. (1)、求证:四边形ABCD是菱形;(2)、若AB= , BD=2,求OE的长.22. 阅读下面的材料,解决问题:
(1)、求证:四边形ABCD是菱形;(2)、若AB= , BD=2,求OE的长.22. 阅读下面的材料,解决问题:像、、、……,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,和、与、与等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.我们把通过适当的变形化去分母中根号的运算叫做分母有理化.
例如:;;
(1)、计算:;;(2)、计算:;(3)、比较和的大小,并说明理由.23. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .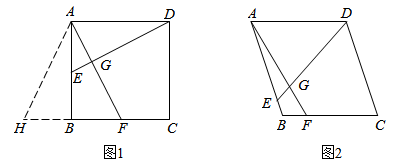 (1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.
(1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.类比迁移:如图2,在菱形 中,点 分别在 边上, 与 相交于点 , ,求 的长.