山东省德州市夏津县2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-05-29 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{a + 2} \cdot \sqrt{a - 2} = \sqrt{a^{2} - 4}$ ，则a的取值范围是（　　）

A、 $a \geq 2$ B、 $a \geq - 2$ C、 $a \geq 24$ D、 $2 \geq a \geq - 2$

查看试题解析
2. 下列运算正确的是（）

A、 $4 \sqrt{3} \times 2 \sqrt{6} = 24 \sqrt{2}$ B、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ C、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ D、 $\sqrt{{(2 - \sqrt{5})}^{2}} = 2 - \sqrt{5}$

查看试题解析
3. 若实数 $m$ 、 $n$ 满足 $| m - 3 | + \sqrt{n - 4} = 0$ ，且 $m$ 、 $n$ 恰好是 $R t △ A B C$ 的两条边长，则第三条边长为（）．

A、5 B、 $\sqrt{7}$ C、5或 $\sqrt{7}$ D、以上都不对

查看试题解析
4. 根据下列条件不能判定三角形是直角三角形的是（　　）

A、 $∠ A ： ∠ B ： ∠ C = 2 ： 3 ： 5$ B、 $a ： b ： c = 5 ： 3 ： 4$ C、 $a = \sqrt{5} ， b = \sqrt{2} ， c = \sqrt{3}$ D、 $∠ A + ∠ B = 2 ∠ C$

查看试题解析
5. 葛藤是一种多年生草本植物，为获得更多的雨露和阳光，其茎蔓常绕着附近的树干沿最短路线盘旋而上．如果把树干看成圆柱体，它的底面周长是50cm，当一段葛藤绕树干盘旋2圈升高为2.4m时，这段葛藤的长是（）m．

A、3 B、2.6 C、2.8 D、2.5

查看试题解析
6. 如图，四边形ABCD的对角线交于点O ，下列哪组条件不能判断四边形ABCD是平行四边形（）

A、OA＝OC ， OB＝OD B、AB＝CD ， AO＝CO C、AB＝CD ， AD＝BC D、∠BAD＝∠BCD ， AB∥CD

查看试题解析
7. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{（ a - 1 ）^{2}}$ - $\sqrt{（ a - b ）^{2}}$ +b的结果是（　　）

A、1 B、b+1 C、2a D、1-2a

查看试题解析
8. 如图，D，E，F分别是 $△ A B C$ 各边的中点， $A H$ 是高，如果 $D E = 6 cm$ ，那么 $H F$ 的长为（）

A、 $6 cm$ B、 $5 cm$ C、 $4 cm$ D、 $3 cm$

查看试题解析
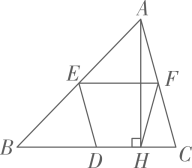9. 如图，在矩形ABCD中，AB＝8，BC＝4.将矩形沿AC折叠，CD′与AB交于点F，则AF：BF的值为（）

A、2 B、 $\frac{5}{3}$ C、 $\frac{5}{4}$ D、 $\sqrt{3}$

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $A D > A B$ ，以点A为圆心， $A B$ 为半径画弧与 $A D$ 交于点F，然后以大于 $\frac{1}{2} B F$ 为半径，分别以B，F为圆心画弧交于点G，连接 $A G$ 交 $B C$ 于点E，若 $B F = 6$ ， $A B = 4$ ，则 $A E$ 的长为（）

A、 $\sqrt{7}$ B、 $2 \sqrt{7}$ C、5 D、10

查看试题解析
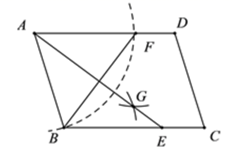11. 如图，菱形ABCD的周长为24，∠ABD＝30°，Q是BC的中点，则PC+ PQ的最小值是（　　）

A、6 B、3 $\sqrt{3}$ C、3 $\sqrt{5}$ D、6 $\sqrt{3}$

查看试题解析
12. 如图，正方形 $A B C D$ 中，点E、F、H分别是 $A B$ 、 $B C$ 、 $C D$ 的中点， $C E$ 、 $D F$ 交于G ，连接 $A G$ 、 $H G$ ．下列结论：① $C E ⊥ D F$ ；② $A G ＝ A D$ ；③ $∠ C H G ＝ ∠ D A G$ ；④ $H G = \frac{1}{2} A D$ ，其中正确的有（　　）

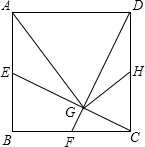A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知x= $\sqrt{5}$ +2，代数x²﹣4x+11的值为．

查看试题解析
14. 已知 $\sqrt{12 n}$ 是整数，则满足条件的最小正整数n为．

查看试题解析
15. 如图，平行四边形 $A B C D$ 中，对角线 $A C 、 B D$ 相交于点 $O$ ，若 $A B = 2 ， B C = 3 ， ∠ A B C = 60^{°}$ ，则图中阴影部分的面积是.

查看试题解析
16. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 ° ， A B = 5 ， A C = 12$ ，点D是 $B C$ 上的一个动点，过点D分别作 $D M ⊥ A B$ 于点M ， $D N ⊥ A C$ 于点N ，连接 $M N$ ，则线段 $M N$ 的最小值为．

查看试题解析
17. 已知：在 $▱ A B C D$ 中， $A E$ 为 $B C$ 边上的高，且 $A E = 12$ ，若 $A B = 15$ ， $A C = 13$ ，则 $▱ A B C D$ 的面积为.

查看试题解析
18. 如图是高空秋千的示意图，小明从起始位置点A处绕着点O经过最低点B，最终荡到最高点C处，若∠AOC=90°，点A与点B的高度差AD=1米，水平距离BD=4米，则点C与点B的高度差CE为米。

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{27} \div \sqrt{3} - \sqrt{\frac{2}{3}} \times \sqrt{12} + \sqrt{18}$ ；

(2)、 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) - {(\sqrt{3} + 2)}^{2}$

查看试题解析
20. 先化简，再求值： $(\frac{x^{2}}{x - 2} + \frac{4}{2 - x}) \div \frac{x^{2} + 4 x + 4}{x}$ .其中 $x = \sqrt{2} - 2$ .

查看试题解析
21. 如图，点E、F是平行四边形ABCD对角线AC上两点， $B E ∥ D F$ .

(1)、求证： $A F = C E$ ；

(2)、若 $A C = 8$ ， $B C = 6$ ， $∠ A C B = 30 °$ ，求平行四边形ABCD的面积.

查看试题解析
22. 如图，一架 $2.5 m$ 长的梯子 $A B$ 斜靠在一竖直墙 $A O$ 上，这时 $A O$ 为 $2.4 m$ .

(1)、求 $O B$ 的长度；

(2)、如果梯子底端 $B$ 沿地面向外移动 $0.8 m$ 到达点 $C$ ，那么梯子顶端 $A$ 下移多少 $m$ ？

查看试题解析
23. 如图，在矩形ABCD中， $A B = 8$ cm， $B C = 16$ cm，点P从点D出发向点A运动，运动到A停止，同时，点Q从点B出发向点C运动，运动到点C即停止，点P ， Q的速度都是1cm/s．连接PQ ， AQ ， CP ．设点P ， Q运动的时间为ts．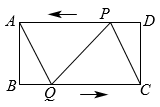

(1)、当t为何值时，四边形ABQP是矩形；

(2)、当t为何值时，四边形AQCP是菱形；

(3)、分别求出（2）中菱形AQCP的周长和面积．

查看试题解析
24. 著名数学教育家G·波利亚，有句名言：“发现问题比解决问题更重要”，这句话启发我们：要想学会数学，就需要观察，发现问题，探索问题的规律性东西，要有一双敏锐的眼睛．请先阅读下列材料，再解决问题：
数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去里面的一层根号．例如： $\sqrt{3 + 2 \sqrt{2}} = \sqrt{1 + 2 \times 1 \times \sqrt{2} + 2} = \sqrt{1^{2} + 2 \times 1 \times \sqrt{2} + {(\sqrt{2})}^{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$ ．

解决问题：

(1)、在括号内填上适当的数： $\sqrt{14 + 6 \sqrt{5}} = \sqrt{9 + 2 \times 3 \times \sqrt{5} + ①} = \sqrt{{(3 + ②)}^{2}} = ③$
①：， ②：， ③ ．

(2)、根据上述思路，求出 $\sqrt{28 - 10 \sqrt{3}} + \sqrt{7 + 4 \sqrt{3}}$ 的值．

查看试题解析
25. 如图： $△ A B D ， △ A P E$ 和 $△ B P C$ 均为直线AB同侧的等边三角形，点P在 $△ A B D$ 内．

(1)、求证：四边形PEDC为平行四边形；

(2)、当点P同时满足条件：① $P A = P B$ 和② $∠ A P B = 150 °$ 时，猜想四边形PEDC是什么特殊的四边形，并说明理由；

(3)、若 $△ A P B$ 中， $A B = 3 ， P A = \sqrt{5} ， P B = 2$ ，求四边形PEDC的面积．

查看试题解析