江西省宜春市2022-2023学年八年级下学期数学期中试卷

试卷更新日期：2023-05-29 类型：期中考试

进入出卷网下载

一、单选题

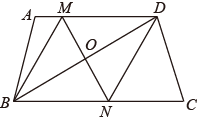
1. 一次函数y＝x﹣1的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{2}{5}}$ B、 $\sqrt{8 x}$ C、 $\sqrt{x^{2} - y^{2}}$ D、 $\sqrt{6 x^{3}}$

查看试题解析
3. 下列各式计算正确的是（　　）

A、 $\sqrt{2} - 2 \sqrt{2} = - \sqrt{2}$ B、 $\sqrt{8 a^{2}} = 4 a$ （a＞0） C、 $\sqrt{(- 4) \times (- 9)} = \sqrt{- 4} \times \sqrt{- 9}$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$

查看试题解析
4. 如图，在 $▱ A B C D$ 中， $B F$ 平分 $∠ A B C$ ，交 $A D$ 于点F ， $C E$ 平分 $∠ B C D$ ，交 $A D$ 于点E ， $A B = 6$ ， $E F = 2$ ，则 $B C$ 的长为（）

A、4 B、6 C、8 D、10

查看试题解析
5. 长方形花园长 $80$ 米，宽比长短 $20$ 米，把对角线修成一条小路，这条小路的长为（）

A、 $60$ 米 B、 $100$ 米 C、 $130$ 米 D、 $150$ 米

查看试题解析
6. 已知正比例函数 $y = k x (k \neq 0)$ 的图象过点 $(2 ， 3)$ ，把正比例函数 $y = k x (k \neq 0)$ 的图象平移，使它过点 $(1 ， - 1)$ ，则平移后的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 计算 $\sqrt{27} - 6 \sqrt{\frac{1}{3}}$ 的结果是.

查看试题解析
8. 若 $\sqrt{3}$ 的整数部分为x，小数部分为y，则 $\sqrt{3} x - y$ 的值是．

查看试题解析
9. 用一条长为 $24 cm$ 的铁丝围成一个斜边长为 $10 cm$ 的直角三角形，则两条直角边的长分别是 $cm$ 和 $cm$ ．

查看试题解析
10. 如图所示的网格是正方形网格，则 $∠ P A B ＋ ∠ P B A$ ＝°（点A，B，P是网格线交点）.

查看试题解析
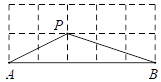11. 如图，在四边形ABCD中，点P是对角线BD的中点，点E、F分别是AB、CD的中点，AD=BC，∠PEF=30°，则∠PFE的度数是．

查看试题解析
12. 如图，在▱ $A B C D$ 中， $A B = 4 cm$ ， $A D = 12 cm$ ，点P在边 $A D$ 上以每秒 $1 cm$ 的速度从点A向点D运动，点Q在边 $B C$ 上以每秒 $3 cm$ 的速度从点C出发，在 $C B$ 间往返运动．两个点同时出发，当点P到达点D时停止运动（同时点Q也停止运动）．在这段时间内，当运动时间为时，线段 $P Q ∥ A B$ ．

查看试题解析

三、解答题

13. 计算：

(1)、 $(\sqrt{8} + \sqrt{3}) \times \sqrt{6} - \sqrt{\frac{1}{2}}$ ；

(2)、 $\sqrt{1.6} \div \sqrt{1 \frac{1}{5}} - {(2023)}^{0} + | \sqrt{3} - 2 |$ ．

查看试题解析
14. 先化简，再求值： $\frac{4 (x^{2} - x)}{x - 1}$ +（x-2）²-6 $\cdot$ $\sqrt{\frac{x^{2}}{9}}$ ，其中，x= $\sqrt{5}$ +1．

查看试题解析
15. 如图1，荡秋千是中国古代北方少数民族创造的一种运动．有一天，小明在公园里游玩，如图2，他发现秋千静止时，踏板离地的垂直高度 $D E = 1 m$ ，将它往前推送 $6 m$ （水平距离 $B C = 6 m$ ）时，秋千的踏板离地的垂直高度 $B F = C E = 3 m$ ，秋千的绳索始终拉得很直，求绳索 $A D$ 的长度？

查看试题解析
16. 如图，在□ABCD中，点E在BC上，AB=BE ， BF平分∠ABC交AD于点F ，请用无刻度的直尺画图（保留作图痕迹，不写画法）.

(1)、在图1中，过点A画出△ABF中BF边上的高AG；

(2)、在图2中，过点C画出C到BF的垂线段CH.

查看试题解析
17. 小军到某景区游玩，他从景区入口处步行到达小憩屋，休息片刻后继续前行，此时观光车从景区入口处出发的沿相同路线先后到达观景点，如图， $l_{1}$ ， $l_{2}$ 分别表示小军与观光车所行的路程 $y (m)$ 与时间 $x (\min)$ 之间的关系.
根据图象解决下列问题：

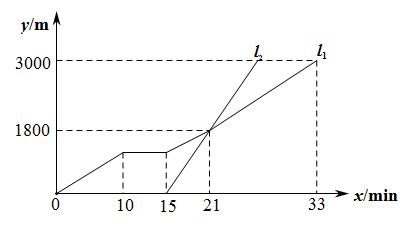(1)、观光车出发分钟追上小军；

(2)、求 $l_{2}$ 所在直线对应的函数表达式；

(3)、观光车比小军早几分钟到达观景点？请说明理由.

查看试题解析
18. 如图，在 $△ A B C$ 中， $A C = \sqrt{3}$ ， $A B = \sqrt{2}$ ， E是边 $B C$ 的中点，且 $A E = \frac{\sqrt{5}}{2}$ ．求证： $△ A B C$ 是直角三角形．

查看试题解析
19. 如图，在四边形ABCD中， $A D ∥ B C$ ，对角线 $B D$ 的垂直平分线与边 $A D$ 、 $B C$ 分别相交于点M、N ．

(1)、求证：四边形 $B N D M$ 是菱形；

(2)、若菱形 $B N D M$ 的周长为 $52 ， M N = 10$ ，求菱形 $B N D M$ 的面积．

查看试题解析
20. 如图，直线 $A B$ 过点 $A (- 1 ， 5)$ ， $P (2 ， a)$ ， $B (3 ， - 3)$ ．

(1)、求直线 $A B$ 的函数解析式和a的值；

(2)、直线 $A B$ 分别与x轴，y轴交于点C，D，求点C，D的坐标；

(3)、求 $△ A O P$ 的面积

查看试题解析
21. 如图，已知锐角 $△ A B C$ 中， $C D ， B E$ 分别是 $A B ， A C$ 边上的高， $M ， N$ 分别是线段 $B C ， D E$ 的中点．

(1)、求证： $M N ⊥ D E$ ；

(2)、若 $∠ A B C = 70 ° ， ∠ A C B = 50 °$ ，连结 $D M ， M E$ ，求 $∠ D M E$ 的度数；

(3)、猜想 $∠ D M E$ 与 $∠ A$ 之间的关系，并证明你的猜想．

查看试题解析