河北省唐山市乐亭县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 对下面问题的调查,适合用普查方式的是( ).A、了解我国七年级学生的视力情况 B、了解一批圆珠笔芯的使用寿命 C、对“天舟五号”货运飞船零部件的检查 D、中央电视台春节联欢晚会的收视率2. 在平面直角坐标系中,点一定在( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,把两根木条AB和AC的一端A用螺栓固定在一起,木条AC自由转动至位置.在转动过程中,下面的量是常量的为( )
 A、的度数 B、BC的长度 C、C的面积 D、AC的长度4. 为了解我校初三年级所有同学的数学成绩,从中抽出500名同学的数学成绩进行调查,抽出的500名考生的数学成绩是( )A、总体 B、样本 C、个体 D、样本容量5. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
A、的度数 B、BC的长度 C、C的面积 D、AC的长度4. 为了解我校初三年级所有同学的数学成绩,从中抽出500名同学的数学成绩进行调查,抽出的500名考生的数学成绩是( )A、总体 B、样本 C、个体 D、样本容量5. 如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )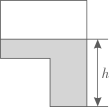 A、
A、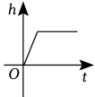 B、
B、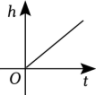 C、
C、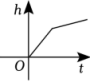 D、
D、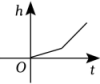 6. 函数中,自变量x的取值范围是( )A、 B、且 C、 D、且7. 小亮同学想要统计最受本班学生欢迎的北京冬奥会运动项目,以下是打乱的统计步骤.①根据统计表绘制条形统计图;②制作调查问卷,对全班同学进行问卷调查;③从条形统计图中分析出最受欢迎的冬奥会项目;④整理问卷调查数据并绘制统计表.正确的统计步骤顺序是( )A、④③②① B、②①③④ C、②④①③ D、②④③①8. 在平面直角坐标系中,点在y轴上,则点A的坐标为( )A、 B、 C、 D、9. 一组数据的最大值是100,最小值是45,若选取组距为10,则这组数据可分成( )A、6组 B、7组 C、8组 D、9组10. 若点 , 关于x轴对称,则a , b的值分别为( )A、 , B、 , C、 , D、 ,11. 在平面直角坐标系中,将点 向右平移 个单位长度后得到的点的坐标为( )A、 B、 C、 D、12. 如图,在x轴,y轴上分别截取 , , 使 , 再分别以点A , B为圆心,以大于长为半径画弧,两弧交于点P . 若点P的坐标为 , 则a的值为( ).
6. 函数中,自变量x的取值范围是( )A、 B、且 C、 D、且7. 小亮同学想要统计最受本班学生欢迎的北京冬奥会运动项目,以下是打乱的统计步骤.①根据统计表绘制条形统计图;②制作调查问卷,对全班同学进行问卷调查;③从条形统计图中分析出最受欢迎的冬奥会项目;④整理问卷调查数据并绘制统计表.正确的统计步骤顺序是( )A、④③②① B、②①③④ C、②④①③ D、②④③①8. 在平面直角坐标系中,点在y轴上,则点A的坐标为( )A、 B、 C、 D、9. 一组数据的最大值是100,最小值是45,若选取组距为10,则这组数据可分成( )A、6组 B、7组 C、8组 D、9组10. 若点 , 关于x轴对称,则a , b的值分别为( )A、 , B、 , C、 , D、 ,11. 在平面直角坐标系中,将点 向右平移 个单位长度后得到的点的坐标为( )A、 B、 C、 D、12. 如图,在x轴,y轴上分别截取 , , 使 , 再分别以点A , B为圆心,以大于长为半径画弧,两弧交于点P . 若点P的坐标为 , 则a的值为( ). A、1 B、 C、3 D、13. 将的三个顶点的纵坐标不变,横坐标均乘以后得到 , 则( ).A、与关于x轴对称 B、与关于y轴对称 C、与关于原点对称 D、向x轴的负方向平移了一个单位14. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度h(米)与小强出发后的时间t(分钟)的函数关系如图所示,下列结论正确的是:( )
A、1 B、 C、3 D、13. 将的三个顶点的纵坐标不变,横坐标均乘以后得到 , 则( ).A、与关于x轴对称 B、与关于y轴对称 C、与关于原点对称 D、向x轴的负方向平移了一个单位14. 小强和爷爷去爬山,爷爷先出发一段时间后小强再出发,途中小强追上了爷爷并最终先爬到山顶,两人所爬的高度h(米)与小强出发后的时间t(分钟)的函数关系如图所示,下列结论正确的是:( ) A、爷爷比小强先出发20分钟 B、小强爬山的速度是爷爷的2倍 C、表示的是爷爷爬山的情况,表示的是小强爬山的情况 D、山的高度是480米15. 在平面直角坐标系中,第一象限内的点到y轴的距离是5,则a的值为( )A、 B、2或 C、2 D、816. 如图1,在中, , 点D是的中点,动点P从点C出发沿运动到点B , 设点P的运动路程为x , 的面积为y , y与x的函数图象如图2所示,则的长为( ).
A、爷爷比小强先出发20分钟 B、小强爬山的速度是爷爷的2倍 C、表示的是爷爷爬山的情况,表示的是小强爬山的情况 D、山的高度是480米15. 在平面直角坐标系中,第一象限内的点到y轴的距离是5,则a的值为( )A、 B、2或 C、2 D、816. 如图1,在中, , 点D是的中点,动点P从点C出发沿运动到点B , 设点P的运动路程为x , 的面积为y , y与x的函数图象如图2所示,则的长为( ). A、 B、10 C、5 D、
A、 B、10 C、5 D、二、填空题
-
17. 某校对1000名学生的身高进行了测量,身高在(单位:m)这一小组的频率为0.26,则该组的人数为 .18. 校园里栽下一棵1.8米高的小树,以后每年生长0.3米,则n年后的树高L与年数n之间的函数关系式是 .19. 如下图所示,在平面直角坐标系中,点P的坐标为 , 点Q是x轴上的一个动点,当线段的长最小时,点Q的坐标为 .
 20. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.
20. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.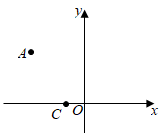
三、解答题
-
21. 由于疫情的影响,学生不能返校上课,沙坪坝区某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、在扇形统计图中,m的值是 , D对应的扇形圆心角的度数是;(3)、请补全条形统计图.22. 某市出租车收费标准如下:3千米以内(含3千米)收费8元;超过3千米的部分每千米收费1.6元,当出租车行驶路程为x千米时,应收费为y元.(1)、请写出当时,y与x之间的关系式;(2)、小亮乘出租车行驶5千米,应付多少元?(3)、小亮付车费19.2元,出租车行驶了多少千米?23. 已知,如图,方格纸中每个小方格都是边长为1个单位长度的正方形,现有A , B , C三点,其中点A坐标为 , 点B坐标为 . (1)、请根据点A , B的坐标在方格纸中建立平面直角坐标系,并直接写出点C坐标为;(2)、若点C关于直线的对称点为点D , 则点D的坐标为;(3)、在y轴上找一点F , 使的面积等于的面积,点F的坐标为 .24. 一个蓄水池有水 , 打开放水闸门放水,水池里的水量和放水时间x(分)的关系如下表.
(1)、请根据点A , B的坐标在方格纸中建立平面直角坐标系,并直接写出点C坐标为;(2)、若点C关于直线的对称点为点D , 则点D的坐标为;(3)、在y轴上找一点F , 使的面积等于的面积,点F的坐标为 .24. 一个蓄水池有水 , 打开放水闸门放水,水池里的水量和放水时间x(分)的关系如下表.放水时间x/分
1
2
3
4
…
水池里的水量
48
46
44
42
…
(1)、在上表中,自变量是 , 因变量是;(2)、观察表格,可得:蓄水池每分钟放水 , 水池里的水量y与放水时间x的关系式为;(3)、当x为何值时,水池里的水可全部放完?25. 先阅读一段文字,再回答下列问题:已知在平面内两点坐标 , , 其两点间距离公式为 .
例如:点和的距离为 . 同时,当两点所在的直线在坐标轴上或平行于x轴或平行于y轴距离公式可简化成:或 .
(1)、已知A、B在平行于y轴的直线上,点A的纵坐标为 , 点B的纵坐标为 , 则A,B两点的距离为;(2)、线段平行于x轴,且 , 若点B的坐标为 , 则点A的坐标是;(3)、已知 , , A , B两点的距离为;(4)、已知三个顶点坐标为 , , , 请判断此三角形的形状,并说明理由.26. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论: (1)、A , B两城相距千米;甲车的速度为 , 乙车的速度为;(2)、乙车出发小时后追上甲车;(3)、当甲、乙两车相距50千米时,t= .
(1)、A , B两城相距千米;甲车的速度为 , 乙车的速度为;(2)、乙车出发小时后追上甲车;(3)、当甲、乙两车相距50千米时,t= .