河北省保定市雄县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-05-29 类型:期中考试
一、单选题
-
1. 下列各数中,能使二次根式在实数范围内有意义的是( )A、 B、 C、 D、2. 在二次根式 , , , 中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个3. 由下列各组线段围成的三角形中,是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列命题的逆命题是假命题的是( )A、等角对等边 B、全等三角形的对应角相等 C、直角三角形的两个锐角互余 D、平行四边形的两组对边分别相等5. 如图,在平面直角坐标系中,点A的坐标为 , 以为一边作正方形 , 则点B的坐标为( )
 A、 B、 C、或 D、或6. 能与相乘得1的是( )A、 B、 C、 D、7. 要使如图所示的四边形是平行四边形,根据图中数据,可以添加的条件是( )
A、 B、 C、或 D、或6. 能与相乘得1的是( )A、 B、 C、 D、7. 要使如图所示的四边形是平行四边形,根据图中数据,可以添加的条件是( ) A、 B、 C、 D、8. 若 , 则的值为( )A、5 B、6 C、10 D、259. 从正面看一个高度为的圆柱体饮料杯子如图所示,在它的正中间竖直插入一根吸管,吸管露出杯子外 , 当吸管伸向杯壁底部时,吸管顶端刚好与杯口高度平齐,则杯子的底面直径为( )
A、 B、 C、 D、8. 若 , 则的值为( )A、5 B、6 C、10 D、259. 从正面看一个高度为的圆柱体饮料杯子如图所示,在它的正中间竖直插入一根吸管,吸管露出杯子外 , 当吸管伸向杯壁底部时,吸管顶端刚好与杯口高度平齐,则杯子的底面直径为( ) A、 B、 C、 D、10. 根据如图所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M , 则点M所表示的数为( )
A、 B、 C、 D、10. 根据如图所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M , 则点M所表示的数为( ) A、-1.7 B、 C、 D、11. 已知 , , 求的值.
A、-1.7 B、 C、 D、11. 已知 , , 求的值.嘉琪同学的解题步骤如下:
………………………………………………①
……………………②
…………………………………………………………③
…………………………………………………………………④
其中,首先出错的步骤是( )
A、① B、② C、③ D、④12. 如图,矩形的两条对角线相交于点O,点E在的延长线上,若 , 则( )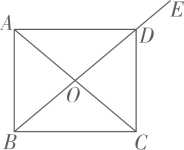 A、 B、 C、 D、13. 如图,在中, , 点D是各边中线的交点,连接并延长,交于点E,连接并延长,交于点F,连接 . 若 , , 则的长为( )
A、 B、 C、 D、13. 如图,在中, , 点D是各边中线的交点,连接并延长,交于点E,连接并延长,交于点F,连接 . 若 , , 则的长为( ) A、2 B、3 C、4 D、514. 如图1,在中, , 为钝角.要在对边 , 上分别找点M,N,使四边形为菱形.现有图2中的甲、乙两种用尺规作图确定点M,N的方案,则可得出结论( )
A、2 B、3 C、4 D、514. 如图1,在中, , 为钝角.要在对边 , 上分别找点M,N,使四边形为菱形.现有图2中的甲、乙两种用尺规作图确定点M,N的方案,则可得出结论( ) A、只有甲正确 B、只有乙正确 C、甲、乙都不正确 D、甲、乙都正确15. 如图,在中, , , 连接 , 相交于点O,E为的中点,若 , 则四边形的面积为( )
A、只有甲正确 B、只有乙正确 C、甲、乙都不正确 D、甲、乙都正确15. 如图,在中, , , 连接 , 相交于点O,E为的中点,若 , 则四边形的面积为( ) A、 B、 C、 D、16. 对于题目:如图1,平面上,正方形内有一个两直角边长分别为2,5的直角三角形,它可以在正方形的内部及边界通过“移转(即平移或旋转)”的方式,自由地从横放移转到竖放,求正方形边长的最小整数值n.甲、乙作了自认为边长最小的正方形,先求出该边长x,再取最小整数值n.
A、 B、 C、 D、16. 对于题目:如图1,平面上,正方形内有一个两直角边长分别为2,5的直角三角形,它可以在正方形的内部及边界通过“移转(即平移或旋转)”的方式,自由地从横放移转到竖放,求正方形边长的最小整数值n.甲、乙作了自认为边长最小的正方形,先求出该边长x,再取最小整数值n.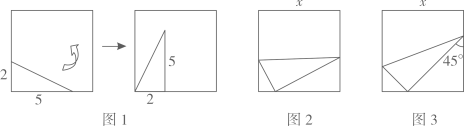
甲:如图2,当x为直角三角形斜边长时就可移转过去,结果取 .
乙:如图3,当x为直角三角形的两条直角边之和的倍时就可移转过去,结果取 .
下列说法正确的是( )
A、甲的思路对,但他的n值错 B、甲的思路和他的n值都对 C、乙的思路对,但他的n值错 D、甲和乙的思路都错二、填空题
-
17. 化简: .18. 如图,把形如的纸沿直线折叠,若直角边 , 斜边 , 则
 (1)、BC=;(2)、不重叠部分(阴影部分所示的三个小三角形)的周长为 .19. 在一个正方形的内部按照如图所示的方式放置大小不同的两个小正方形,其中较小的正方形面积为10,重叠部分的面积为3,则:
(1)、BC=;(2)、不重叠部分(阴影部分所示的三个小三角形)的周长为 .19. 在一个正方形的内部按照如图所示的方式放置大小不同的两个小正方形,其中较小的正方形面积为10,重叠部分的面积为3,则: (1)、较小正方形的边长为 .(2)、设两处空白部分的面积分别为 , ,
(1)、较小正方形的边长为 .(2)、设两处空白部分的面积分别为 , ,①;(填>, <或=)
②若 , 则正方形内部较大的正方形面积为 .
三、解答题
-
20. 嘉琪同学计算: , 部分解题步骤如下.
解: .
(1)、在以上解题步骤中用到了______________(从下面选项中选出两个).A、等式的基本性质 B、二次根式的化简 C、二次根式的乘法法则 D、通分(2)、算到这里,他发现算式好像变得更复杂了,请用一种简便的方法解答此题.21. 如图,在的正方形网格图中,所有小正方形的边长均为1,点A,B为格点,格点C到点A的距离最长. (1)、画出线段 , 并求出的长度.(2)、求点B到直线的距离.22. 如图,为的中位线,在外取点F,连接 , , , 与相交于点 , , .
(1)、画出线段 , 并求出的长度.(2)、求点B到直线的距离.22. 如图,为的中位线,在外取点F,连接 , , , 与相交于点 , , . (1)、求证:四边形是平行四边形.(2)、若 , , , 求的周长.23. 如图,在正方形和中,点B,C,G在同一条直线上,P是线段的中点,连接 , 连接并延长,交于点Q.请证明:
(1)、求证:四边形是平行四边形.(2)、若 , , , 求的周长.23. 如图,在正方形和中,点B,C,G在同一条直线上,P是线段的中点,连接 , 连接并延长,交于点Q.请证明: (1)、四边形是矩形.(2)、当时,四边形是正方形.24. 在算式“”中,“”表示被开方数,“”表示“”“”“”“”中的某一个运算符号.(1)、当“”表示“”时,运算结果为 , 求“”表示的数.(2)、如果“”表示的是(1)中所求的数,请通过计算说明当“”表示哪一种运算符号时,算式的结果最大.25. 教材中有这样一道题:如图1,四边形是正方形,G是上的任意一点,于点E, , 且交于点F.求证: .
(1)、四边形是矩形.(2)、当时,四边形是正方形.24. 在算式“”中,“”表示被开方数,“”表示“”“”“”“”中的某一个运算符号.(1)、当“”表示“”时,运算结果为 , 求“”表示的数.(2)、如果“”表示的是(1)中所求的数,请通过计算说明当“”表示哪一种运算符号时,算式的结果最大.25. 教材中有这样一道题:如图1,四边形是正方形,G是上的任意一点,于点E, , 且交于点F.求证: .
小明通过证明解决了问题,在此基础上他进一步提出了以下以下回题,请你解答.
(1)、若图1中的点G为延长线上一点,其余条件不变,如图2所示,猜想此时 , , 之间的数量关系,并证明你的结论.(2)、将图1中的绕点A逆时针旋转,使得与重合,记此时点F的对应点为点 , 如图3所示,若正方形的边长为3,求的长度.26. 已知等边三角形的边长为12,D为射线上一动点(点D不与B,C重合),以为边作菱形 , 使 , 连接 . (1)、如图,当点D在边上时,求证: ,(2)、在点D的移动过程中,当时,求的长度(3)、设与菱形的面积分别为 , , 直接写出的最大值.
(1)、如图,当点D在边上时,求证: ,(2)、在点D的移动过程中,当时,求的长度(3)、设与菱形的面积分别为 , , 直接写出的最大值.