广东省深圳市深大附中集团2022-2023学年八年级下学期数学期中联考试卷

试卷更新日期：2023-05-29 类型：期中考试

进入出卷网下载

一、单选题

1. 垃圾分类人人有责．下列垃圾分类标识是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $x > y$ ，则下列不等式成立的是（）

A、 $- 2 x > - 2 y$ B、 $x - 6 < y - 6$ C、 $x - y < 0$ D、 $\frac{x}{5} > \frac{y}{5}$

查看试题解析
3. 如图，△ABC沿BC方向平移后的得到△DEF ，已知BC=5，EC=2，则平移的距离是（　　）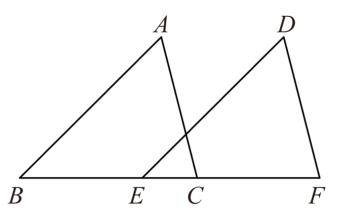

A、1 B、2 C、3 D、4

查看试题解析
4. 已知 $x - y = - 2$ ， $x y = 3$ ，则 $x^{2} y - x y^{2}$ 的值为（）

A、2 B、-6 C、5 D、-36

查看试题解析
5. 在 $△ A B C$ 中， $∠ A ： ∠ B ： ∠ C = 1 ： 1 ： 2$ ，边 $B C = 4 cm$ ，则边 $A B$ 的长为（）

A、 $4 cm$ B、 $6cm$ C、 $4 \sqrt{2} cm$ D、 $8cm$

查看试题解析
6. 某学校举行“创新杯”篮球比赛，比赛方案规定：每场比赛都要分出胜负，每队胜1场积2分，负1场积1分，每只球队在全部8场比赛中积分不少于12分，才能获奖．小明所在球队参加了比赛并计划获奖，设这个球队在全部比赛中胜x场，则x应满足的关系式是（）

A、 $2 x + (8 - x) \geq 12$ B、 $2 x + (8 - x) \leq 12$ C、 $2 x - (8 - x) \geq 12$ D、 $2 x > 12$

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=2，AB=6，则△ABD的面积是（）

A、3 B、6 C、12 D、18

查看试题解析
8. 已知一次函数 $y = k x + b$ （k、b为常数）的图象如图所示，那么关于x的不等式 $k x + b > 0$ 的解集是（　　）

A、 $x > 0$ B、 $x < 0$ C、 $x < 2$ D、 $x > 2$

查看试题解析
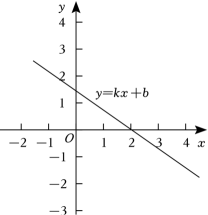9. 如图，把一张长方形纸片沿对角线折叠，若 $∠ E D F = 30^{\circ}$ ，则长方形纸片的长宽比为（）

A、2：1 B、 $\sqrt{2}$ ：1 C、 $\sqrt{3}$ ：1 D、2： $\sqrt{3}$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 2$ ， D为 $B C$ 的中点， $D E ⊥ A B$ ，垂足为E ．过点B作 $B F ∥ A C$ 交 $D E$ 的延长线于点F ，连接 $C F ， A F$ ；现有如下结论：

① $A D$ 平分 $∠ C A B$ ；② $B F = 1$ ；③ $A D ⊥ C F$ ；④ $A F = \sqrt{5}$ ；⑤ $∠ C A F = ∠ C F B$ ．其中正确的结论有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 分解因式： $x (x - 3) + (3 - x) =$ ．

查看试题解析
12. 如图，等腰三角形ABC中， $A B = A C$ ， $∠ A = 50^{\circ}$ ， $C D ⊥ A B$ 于D ，则 $∠ D C B$ 等于．

查看试题解析
13. 已知 x＞2 是关于 x 的不等式 x－3m＋1＞0 的解集，那么m 的值为．

查看试题解析
14. 如图，直角△ABC沿着点B到点C的方向平移到△DEF的位置，AB=4，DH=1，平移距离为2，则阴影部分的面积是．

查看试题解析
15. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B =60 °$ ， $B C = 1$ ，点P为 $A B$ 边上任意一点，连接 $P C$ ，以C为中心将 $P C$ 按逆时针方向旋转 $60 °$ 得 $Q C$ ，连接 $A Q$ ，则 $A Q$ 的最小值为．

查看试题解析

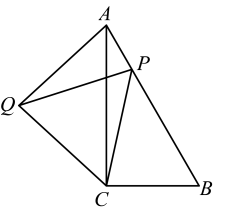
三、解答题

16. 解不等式组，并求其整数解；
${\begin{matrix} x - 3 (x - 2) \leq 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ ．

查看试题解析
17. 因式分解：

(1)、 $2 x^{2} - 4 x + 2$

(2)、 ${(x - y)}^{3} - 16 (x - y)$

查看试题解析
18. 如图，在平面直角坐标中， $△ A B C$ 的顶点坐标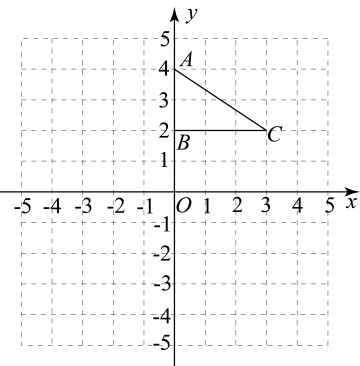分别是 $A (0 ， 4) ， B (0 ， 2) ， C (3 ， 2)$ ．

(1)、将 $△ A B C$ 以O为旋转中心旋转 $180^{\circ}$ ，画出旋转后对应的 $Δ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A B C$ 平移后得到 $Δ A_{2} B_{2} C_{2}$ ，若点A的对应点 $A_{2}$ 的坐标为 $(2 ， 2)$ ，画出平移后对应的 $Δ A_{2} B_{2} C_{2}$ ；

(3)、求线段 $C_{1} C_{2}$ 的长度．

查看试题解析
19. 某工程队承担了一段长为1500米的道路绿化工程，施工时有两种绿化方案：甲方案是绿化1米的道路需要A型花2枝和B型花3枝，成本是22元；乙方案是绿化1米的道路需要A型花1枝和B型花5枝，成本是25元.现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.

(1)、求A型花和B型花每枝的成本分别是多少元?

(2)、求当按甲方案绿化的道路总长度为多少米时，所需工程的总成本最少?总成本最少是多少元?

查看试题解析
20. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法等等．
①分组分解法：
例如：x²－2xy＋y²－4＝(x²－2xy＋y²)－4＝(x－y)²－2²＝(x－y－2)(x－y＋2)．
②拆项法：
例如：x²＋2x－3＝x²＋2x＋1－4＝(x＋1)²－2＝(x＋1－2) (x＋1＋2) ＝ (x－1) (x＋3)．

(1)、分解因式：
①4x²＋4x－y²＋1；
②x²－6x＋8；

(2)、已知：a、b、c为△ABC的三条边，a²＋b²＋c²－4a－4b－6c＋17＝0，求△ABC的周长．

查看试题解析
21. 如图，点O是等边 $△$ ABC内一点，将CO绕点C顺时针旋转60°得到CD ，连接OD ， AO ， BO ， AD ．

(1)、求证： $△$ BCO≌ $△$ ACD ．

(2)、若OA＝10，OB＝8，OC＝6，求∠BOC的度数．

查看试题解析
22. 班级数学兴趣小组开展“直角三角板拼拼拼”活动．爱思考的小华拿到了两块相同的直角三角板，已知三角板的最小边长为 $10 cm$ ．他先把两块三角板的斜边拼在一起，并画出如图1所示图形．活动一：将一块三角板固定，另一块三角板以 $30^{\circ}$ 角的顶点为中心，按逆时针方向旋转，如图2．

(1)、若旋转到两块三角板较长直角边垂直，连接两 $60^{\circ}$ 角顶点，如图3所示，则△ABD的面积为；

(2)、在旋转过程中，小华想探究两直角顶点连线与 $60^{\circ}$ 角顶点连线的位置关系，设旋转角为α ，若旋转角为α满足 $0 ° < α < 90^{\circ}$ ，则这两条连线有什么位置关系？写出你的结论，并说明理由．

(3)、活动二：将一块三角板固定，另一块直角三角板沿着斜边所在射线向上平移dcm，两直角顶点连线与斜边所在射线交点设为F ，探究：当 $△ A^{'} F C^{'}$ 为等腰三角形时，求d的值为多少？(直接写出答案)

查看试题解析