2023年北师大版数学八年级下学期期末模拟试卷（1）

试卷更新日期：2023-05-28 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列标志中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x^{2} - 4}{x - 2}$ 的值为零，则 $x$ 的值为（）

A、-1 B、2 C、-2 D、2或-2

查看试题解析
3. 若一个n边形内角和为 $540 °$ ，则n的值为（）

A、5 B、6 C、7 D、8

查看试题解析
4. 已知ab＝2，a-2b＝3，则4ab²-2a²b的值是（）

A、6 B、-6 C、12 D、-12

查看试题解析
5. 若 $a < b$ ，则下列各式中一定成立的是（）

A、 $a - 1 < b - 1$ B、 $a c < b c$ C、 $- a < - b$ D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
6. $▱ A B C D$ 中，E，F是对角线 $B D$ 上不同的两点．下列条件中，不能得出四边形 $A E C F$ 一定为平行四边形的是（）

A、 $∠ B A E = ∠ D C F$ B、 $A F ∥ C E$ C、 $A E = C F$ D、 $B E = D F$

查看试题解析
7. 下列各式正确的是（）

A、 $\frac{c}{- a - b} = - \frac{c}{a - b}$ B、 $\frac{c}{- a - b} = - \frac{c}{a + b}$ C、 $\frac{c}{- a + b} = - \frac{c}{a + b}$ D、 $\frac{c}{- a - b} = - \frac{- c}{a - b}$

查看试题解析
8. 3月4日，太原市住建局宣布，本市2022年计划改造老旧小区604个，涉及户数11.6万户．某小区计划在改造时给80户住户安装天然气，住户需共同承担整体初装费30000元，另需缴纳入户费500元/户．根据惠民政策，政府给予该小区住户一定的补贴，这样平均每户的实际费用不超过800元．若设政府给每户的补贴为x元，则x满足的不等式为（）

A、 $\frac{30000}{80} + 500 - x ≥ 800$ B、 $\frac{30000}{80} + 500 + x ≥ 800$ C、 $\frac{30000}{80} + 500 - x \leq 800$ D、 $\frac{30000}{80} + 500 + x \leq 800$

查看试题解析
9. 如图， $D E$ 是 $△ A B C$ 的中位线，过点C作 $C F ∥ B D$ 交 $D E$ 的延长线于点F，则下列结论正确的是（）

A、 $C F < B D$ B、 $E F > D E$ C、 $E F = C F$ D、 $E F = D E$

查看试题解析
10. 如图，AD是 $△ A B C$ 的角平分线，DE⊥AC，垂足为E， $B F ∥ A C$ 交ED的延长线于点F，若DE＝DF，AE＝2BF．下列四个结论：①BC平分∠ABF；② $E F ∥ A B$ ；③AD⊥BC；④AB＝3BF．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空3分，共15分）

11. 分解因式： $3 m^{2} - 3 =$ ．

查看试题解析
12. 如果一个多边形的内角和与外角和相等，那么这个多边形的边数是 .

查看试题解析
13. 如图，直线 $y = 3 x$ 和 $y = k x + 2$ 相交于点 $P (\frac{1}{2} ， b)$ ，则不等式 $3 x \geq k x + 2$ 的解集为.

查看试题解析
14. 如图，已知 $P$ 是 $∠ A O B$ 平分线上一点， $∠ A O P = 15 °$ ， $C P ∥ O B$ 交OA于点C， $P D ⊥ O B$ ，垂足为 $D$ ，且 $P C = 6 ， O D = 12$ ，则 $△ P D O$ 的面积等于．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $∠ A C B = 30 °$ ， $B C = 3$ ．点P为 $B C$ 边上任意一点，连结 $P A$ ，以 $P A$ ， $P C$ 为邻边作 $▱ P A Q C$ ，连结 $P Q$ ，则 $P Q$ 的最小值为．

查看试题解析

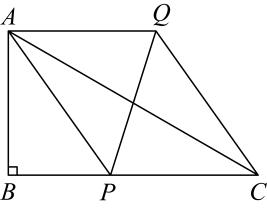
三、作图题（共9分）

16. 如图，方格纸中的每个小方格都是边长为1个单位的小正方形，每个小正方形的顶点称为格点， $△$ ABC的顶点都在格点上，建立如图所示的平面直角坐标系，点A，B，C的坐标分别为(1，1)，(4，2)，(2，3)．

(1)、画出 $△$ ABC向左平移4个单位，再向上平移1个单位后得到的 $△$ A₁B₁C₁；

(2)、画出 $△$ ABC关于原点O对称的 $△$ A₂B₂C₂；

(3)、求 $△$ ABC面积．

查看试题解析

四、解答题（共6题，共46分）

17. 解不等式组 ${\begin{array}{l} 5 x + 1 \geq 3 (x + 1) \\ \frac{1}{2} x < 8 - \frac{3}{2} x \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
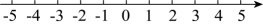18. 先化简： $(a - \frac{3 a}{a + 1}) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ，然后在-2，-1，2三个数中给a选择一个你喜欢的数代入求值．

查看试题解析
19. 某公司计划从商店购买同一品牌的毛巾和同一品牌的香皂，已知购买一条毛巾比购买一块香皂多用20元，若用400元购买毛巾，用160元购买香皂，则购买毛巾的条数是购买香皂块数的一半.

(1)、购买一条该品牌毛巾、一块该品牌香皂各需要多少元？

(2)、经商谈，商店给予该公司购买一条该品牌毛巾赠送一块该品牌香皂的优惠，如果该公司需要香皂的块数是毛巾条数的2倍还多8个，且该公司购买毛巾和香皂的总费用不超过670元，那么该公司最多可购买多少条该品牌毛巾？

查看试题解析
20. 已知：如图，在 $△ A B C$ 中，D、E、F分别是各边的中点， $A H$ 是高．

(1)、四边形 $A D E F$ 是怎样的特殊四边形？证明你的结论：

(2)、问 $∠ D H F$ 与 $∠ D E F$ 有怎样的数量关系？证明你的结论．

查看试题解析
21. 某村在政府的扶持下建起了鲜花大棚基地，准备种植 $A$ ， $B$ 两种鲜花｡经测算，种植两种鲜花每亩的投入与获利情况如下表：

每亩需投入（万元）
每亩可获利（万元）
$A$ 种鲜花
2
0.8
$B$ 种鲜花
4
1.2

(1)、政府和村共同投入200万元全部用来种植这两种鲜花，总获利 $y$ 万元.设种植 $A$ 种鲜花 $x$ 亩，求 $y$ 关于 $x$ 的函数关系式；

(2)、在（1）的条件下，若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍，请你设计出总获利最大的种植方案，并求出最大总获利.

查看试题解析
22. 如图1，已知 $∠ D A C = 90 °$ ， $△ A B C$ 是等边三角形，点 $P$ 为射线 $A D$ 上任意一点（点 $P$ 与点 $A$ 不重合），连接 $C P$ ，将线段 $C P$ 绕点 $C$ 顺时针旋转 $60 °$ 得到线段 $C Q$ ，连接 $Q B$ 并延长交直线 $A D$ 于点 $E$ ．

(1)、如图1，猜想 $∠ Q E P =$ $°$ ．

(2)、如图2、3，若当 $∠ D A C$ 是锐角或钝角时，其它条件不变，猜想 $∠ Q E P$ 的度数，选取一种情况加以证明；

(3)、如图3，若 $∠ D A C = 120 °$ ， $∠ A C P = 15 °$ ，且 $A C = 6$ ，求 $B Q$ 的长．

查看试题解析

	每亩需投入（万元）	每亩可获利（万元）
$A$ 种鲜花	2	0.8
$B$ 种鲜花	4	1.2