2023年北师大版数学七年级下学期期末模拟试卷（4）

试卷更新日期：2023-05-28 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 习近平主席在2022年新年贺词中提到“人不负青山，青山定不负人”，一语道出“人与自然和谐共生”的至简大道．下列有关环保的四个图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a$ 、 $b$ 、 $c$ 为三角形的三边长，且 $a$ 、 $b$ 满足 $| a - 2 | + {(b - 1)}^{2} = 0$ ，则第三边长 $c$ 的值可以是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 $a^{8} \div a^{4} = a^{2}$ D、 ${(- 3 a^{2})}^{2} = 9 a^{4}$

查看试题解析
4. 甲、乙两同学从同一地点同时出发去学校，甲骑自行车，乙步行，甲很快把乙甩在后头，不料自行车坏了，当甲修好自行车后，发现乙已经超过他，于是又奋力追赶，结果甲、乙同时到达学校． $S_{1}$ 、 $S_{2}$ 分别表示乙、甲走的路程，t为去学校的时间，则下列图象与上述情况大致相吻合的是（）

A、 B、 C、 D、

查看试题解析
5. 在 $△ A B C$ 中，如果 $∠ A = 60^{\circ} ， ∠ B = 45^{\circ}$ ，那么 $∠ C$ 等于（）

A、 $115^{\circ}$ B、 $105^{\circ}$ C、 $75^{\circ}$ D、 $45^{\circ}$

查看试题解析
6. 下列事件中是必然事件的是（）

A、打开电视机，正在播放《新闻联播》 B、某种彩票中奖概率为1%，买100张该种彩票一定会有一张中奖 C、投掷一枚质地均匀的硬币100次，正面朝上的次数为50次 D、367个同学参加一个集会，他们中至少有两个同学的生日是同月同日

查看试题解析
7. 如图所示，AB∥CD∥EF，则下列等式中正确的是（）．

A、∠1=180°-∠3 B、∠1=∠3-∠2． C、∠2+∠3=180°-∠1 D、∠2+∠3=180°+∠1

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ B C A = 40 °$ ， $∠ A B C = 60 °$ ．若 $B F$ 是 $△ A B C$ 的高，与角平分线 $A E$ 相交于点 $O$ ，则 $∠ E O F$ 的度数为（）

A、 $130 °$ B、 $70 °$ C、 $110 °$ D、 $100 °$

查看试题解析
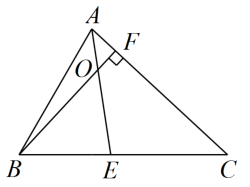9. 如图，现有 $A$ ， $B$ 两类正方形卡片和 $C$ 类长方形卡片各若干张，如果要拼成一个长为 $(m + 2 n)$ ，宽为 $(2 m + n)$ 的大长方形，那么需要 $C$ 类卡片张数为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图， $D C ∥ A B$ ， AE⊥EF，E在BC上，过E作EC⊥DC，EG平分∠FEC，ED平分∠AEC．若∠EAD＋∠BAD＝180°，∠EDA＝3∠CEG，则下列结论：①∠EAB＝2∠FEG；②∠AED＝45°＋∠GEF；③∠EAD＝135°－4∠GEC；④∠EAB＝15°，其中正确的是（）

A、①②③④ B、①③④ C、①②④ D、①②③

查看试题解析

二、填空题（每空3分，共15分）

11. $N 95$ 型口罩可以对空气动力学直径为0.000000075米的颗粒的过滤效率达到95%以上，将0.000000075用科学记数法表示为．

查看试题解析
12. 小颖有两根长度为4cm和9cm的木棒，她想钉一个三角形的木框．现在有5根木棒供她选择，其长度分别为3cm，5cm，10cm，12cm，17cm．小颖随手拿了一根，恰好能够组成一个三角形的概率为．

查看试题解析
13. 如图，在△ABC中，DF，EM分别垂直平分边AB，AC，若△AFM的周长为9，则BC= ．

查看试题解析
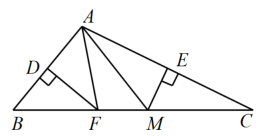14. 如图所示：已知 $∠ A B D = ∠ A B C$ ，请你补充一个条件：，使得 $△ A B D ≅ △ A B C$ .(只需填写一种情况即可)

查看试题解析
15. 计算： ${(- 0.25)}^{2023} \times 4^{2022} =$ ．

查看试题解析

三、解答题（共7题，共55分）

16. 计算：

(1)、 $- 3^{2} + {(- \frac{1}{2})}^{- 2} + {(2021 - π)}^{0} - | - 2 |$

(2)、 $(- 3 a^{2} b) (3 a^{2} b - 2 a b + 4 b^{2}) \div {(2 a b)}^{2}$

(3)、 $202 2^{2} - 2021 \times 2023$

(4)、 $[(2 x + 3 y) (2 x - 3 y) - (2 x - y)^{2}] \div (- \frac{1}{2} y)$ ，其中 $x = 1$ ， $y = \frac{1}{2}$ ．

查看试题解析
17. 完成推理填空：如图在△ABC中，已知∠1+∠2＝180°，∠3＝∠B，试说明∠AED＝∠C．

解：∵∠1+∠2＝180°（         ），

▲ +∠EFD＝180°（邻补角定义），

∴▲ （同角的补角相等）

∴AB∥▲ （内错角相等，两直线平行）

∴∠ADE＝∠3（          ）

∵∠3＝∠B（已知）

∴ ▲ （等量代换）

∴▲ ∥BC（同位角相等，两直线平行）

∴∠AED＝∠C（          ）

查看试题解析
18. 下面网格都是由边长为 $1$ 的小正方形组成，观察如图三个图案（阴影部分），回答下列问题：

(1)、请写出这三个图案的至少两个共同特征；

(2)、请在图④中设计一个图案，使它具备你所写出的特征．

查看试题解析
19. 如图，在四边形ABCD中， $A D ∥ B C$ ，点E在AD上，点F在BC上．

(1)、尺规作图：用没有刻度的直尺和圆规，在四边形内部找一点M，使得点M到AD，AB的距离相等，且 $∠ A M B = 90 °$ ；

(2)、在（1）的条件下，延长AM交BC于点N，且 $A E = N F$ ，连接EF，求证：E，M，F三点共线．

查看试题解析
20. 下表是某商行某商品的销售情况，该商品原价为600元，随着不同幅度的降价（单位：元），日销量（单位：件）发生相应变化如下：
降价（元）
5
10
15
20
25
30
35
日销量（件）
780
810
840
870
900
930
960

(1)、上表反映了哪两个变量之间的关系？哪个是自变量，哪个是因变量？

(2)、每降价5元，日销量增加多少件？降价之前的日销量是多少？

(3)、如果售价为540元时，日销量为多少？

查看试题解析
21. 图1，是一个长为 $2 m$ ，宽为 $2 n$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形.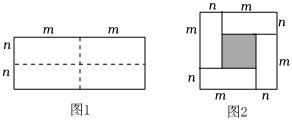

(1)、图2中的阴影部分的面积为；

(2)、观察图2，三个代数式 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 之间的等量关系是；

(3)、若 $x + y = 8$ ， $x y = 6$ ，则 $x - y =$ ； $($ 直接写出答案 $)$

查看试题解析
22. 平面直角坐标系中，O为坐标原点，点A、B分别为x轴正半轴和y轴正半轴上的点，点A（0，5），连接AB ， $S_{△ A O B} = \frac{25}{2}$ ．

(1)、如图1，求点B的坐标；

(2)、如图2，点C为AB中点，点P为线段BC上一动点，点P的纵坐标为m ，连接OC ，若△POC的面积为S ，用含m的式子表示S（不要求写出m的取值范围）；

(3)、如图3，在（2）条件下，点E为y轴点A上方一点，点F为y轴负半轴上一点，AE＝OF ，连接BE ，若射线OP⊥BE于D ，连接PF ， $O P ： P F = 5 ： 7$ ，求点E的坐标．

查看试题解析

降价（元）	5	10	15	20	25	30	35
日销量（件）	780	810	840	870	900	930	960