2023年北师大版数学七年级下学期期末模拟试卷(3)
试卷更新日期:2023-05-28 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 2022年北京和张家口成功举办了第24届冬奥会和冬残奥会.下面关于奥运会的剪纸图片中是轴对称图形的是( )A、
 B、
C、
B、
C、 D、
D、 2. 下列计算正确的是( )A、a3•a2=a5 B、(a3)2=a5 C、a10÷a2=a5 D、a2+a3=a53. 如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( )
2. 下列计算正确的是( )A、a3•a2=a5 B、(a3)2=a5 C、a10÷a2=a5 D、a2+a3=a53. 如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( ) A、三角形具有稳定性 B、三角形内角和等于180° C、两点之间线段最短 D、同位角相等,两直线平行4. 下列事件为必然事件的是( )A、打雷后会下雨 B、明天是晴天 C、哥哥的年龄比弟弟的年龄大 D、下雨后会有彩虹5. 如图所示,在下列四组条件中,不能判定AD∥BC的是( )
A、三角形具有稳定性 B、三角形内角和等于180° C、两点之间线段最短 D、同位角相等,两直线平行4. 下列事件为必然事件的是( )A、打雷后会下雨 B、明天是晴天 C、哥哥的年龄比弟弟的年龄大 D、下雨后会有彩虹5. 如图所示,在下列四组条件中,不能判定AD∥BC的是( )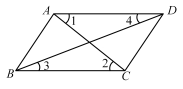 A、∠1=∠2 B、∠3=∠4 C、∠BAD+∠ABC=180° D、∠BAC=∠ACD6. 已知:如图,D、E分别在AB、AC上,若AB=AC,AD=AE,∠A=60°,∠B=25°,则∠BDC的度数是( )
A、∠1=∠2 B、∠3=∠4 C、∠BAD+∠ABC=180° D、∠BAC=∠ACD6. 已知:如图,D、E分别在AB、AC上,若AB=AC,AD=AE,∠A=60°,∠B=25°,则∠BDC的度数是( )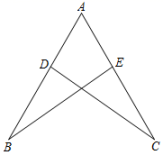 A、95° B、90° C、85° D、80°7. 夏天,一杯开水放在课桌上,杯中水的温度随时间变化的关系可以用哪幅图来近似的刻画( )A、
A、95° B、90° C、85° D、80°7. 夏天,一杯开水放在课桌上,杯中水的温度随时间变化的关系可以用哪幅图来近似的刻画( )A、 B、
B、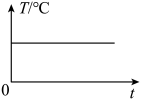 C、
C、 D、
D、 8. 下列语句:①平面内三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行;④两直线被第三条直线所截得的一组同位角的平分线互相平行,其中正确的个数( )A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N , △BCN的周长是7cm,则BC的长为( )
8. 下列语句:①平面内三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行;④两直线被第三条直线所截得的一组同位角的平分线互相平行,其中正确的个数( )A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N , △BCN的周长是7cm,则BC的长为( )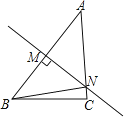 A、1cm B、2cm C、3cm D、4cm10. 如图,有两个正方形 , ,现将 放置在 的内部得到图甲.将 , 并列放置,以正方形 与正方形 的边长之和为新的边长构造正方形得到图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形 , 的面积之和为( )
A、1cm B、2cm C、3cm D、4cm10. 如图,有两个正方形 , ,现将 放置在 的内部得到图甲.将 , 并列放置,以正方形 与正方形 的边长之和为新的边长构造正方形得到图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形 , 的面积之和为( )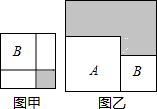 A、13 B、14 C、15 D、16
A、13 B、14 C、15 D、16二、填空题(每空3分,共15分)
-
11. 红细胞是人体中血液运输氧气的主要媒介,人体中红细胞的直径约为0.0000077m,将0.0000077用科学记数法表示为 .12. 已知3a=10,32b=2,则3a﹣2b= .13. 如图,直线 ,三角板的直角顶点A落在直线a上,两条边分别交直线b于B , C两点.若 ,则 度.
 14. 一名老师带领x名学生到青青世界参观,已知成人票每张60元,学生票每张40元设门票的总费用为y元,则y与x的关系式为 .15. 如图所示,将长方形纸片折叠,使点与点重合,点落在点处,折痕为 , 若 , 那么的度数为 .
14. 一名老师带领x名学生到青青世界参观,已知成人票每张60元,学生票每张40元设门票的总费用为y元,则y与x的关系式为 .15. 如图所示,将长方形纸片折叠,使点与点重合,点落在点处,折痕为 , 若 , 那么的度数为 .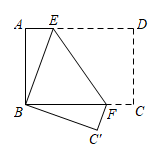
三、计算题(共2题,共14分)
-
16. 计算(1)、(2)、(3)、17. 先化简,再求值:(a+2b) (a-2b)+(a-2b)2 , 其中 a=2,b=-1.
四、解答题(共5题,共41分)
-
18. 一口袋中有5张完全相同的卡片,分别写有1cm、2cm、3cm、4cm和5cm,口袋外有2张卡片,分别写有3cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度.(1)、求这三条线段能构成三角形的概率;(2)、求这三条线段能构成等腰三角形的概率.19. 把下列步骤推理的依据填在步骤后面的括号里.(1)、如图(a)所示,
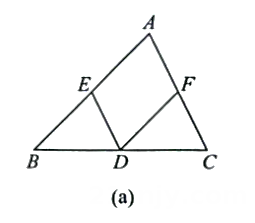
已知FD∥AB,ED∥AC.
∵DF∥AB,
∴∠FDE=∠BED ( )
∵DE∥AC,
∴∠BED= =∠A ( )
∴∠FDE=∠A ( ).
(2)、如图(b)所示,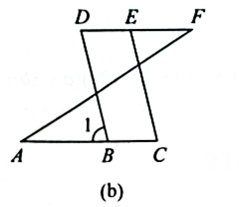
已知∠A =∠F,∠C=∠D.
∵∠A =∠F,
∴AC∥DF ( )
∴∠D=∠1 ( )
又∵∠C=∠D,
∴∠1 =∠C ( ).
∴BD∥CE ( ).
20. 某校七年级学生到野外活动,为测量一池塘两端A , B的距离,甲、乙、丙三位同学分别设计出如下几种方案: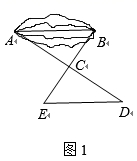
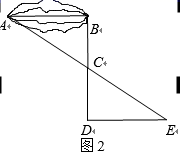
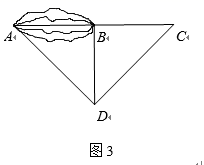
甲:如图①,先在平地取一个可直接到达A , B的点C , 再连接AC , BC , 并分别延长AC至D , BC至E , 使DC=AC , EC=BC , 最后测出DE的长即为A , B的距离.
乙:如图②,先过点B作AB的垂线,再在垂线上取C , D两点,使BC=CD , 接着过点D作BD的垂线DE , 交AC的延长线于点E , 则测出DE的长即为A , B的距离.
丙:如图③,过点B作BD⊥AB , 再由点D观测,在AB的延长线上取一点C , 使∠BDC=∠BDA , 这时只要测出BC的长即为A , B的距离.
(1)、以上三位同学所设计的方案,可行的有;(2)、请你选择一可行的方案,说说它可行的理由.21. 晚上7点15分,小李骑自行车从家出发到距离家3500米远的水上公园看7点40分开始的水上灯光秀,如图所示是小李从家到公园路途中离家的距离与离家时间之间的关系.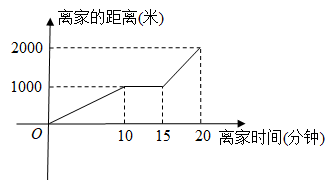 (1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?22. 已知 , 点A在射线CE上,把沿AB翻折得 , .
(1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?22. 已知 , 点A在射线CE上,把沿AB翻折得 , . (1)、若 , 则的度数为°;(2)、设 , ,
(1)、若 , 则的度数为°;(2)、设 , ,①如图1,当点D在直线CE左侧时,求y与x的数量关系,并写出x的取值范围;
②如图2,当点D在直线CE右侧时出y与x的数量关系是 ▲ ;
(3)、过点D作//交CE于点F,当时,求的度数.