2023年北师大版数学七年级下学期期末模拟试卷（2）

试卷更新日期：2023-05-28 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 2022年2月4日中国将举办第24届冬季奥林匹克运动会，这是中国历史上第一次举办冬季奥运会，下面是本届冬奥会及往届冬奥会的会徽，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某种细菌的半径是0.000 0036毫米，这个数用科学记数法可表示为（）

A、3.6×10^﹣⁶毫米 B、3.6×10^﹣⁵毫米 C、0.36×10^﹣⁷毫米 D、36×10^﹣⁴毫米

查看试题解析
3. 下面每组数分别是三根小木棒的长度，它们能摆成三角形的是（）

A、12cm， 3cm， 6cm B、8cm， 16cm， 8cm C、6cm， 6cm， 13cm D、2cm， 3cm， 4cm

查看试题解析
4. 下列事件中，是必然事件的为（）

A、将油滴入水中，油会浮在水面上 B、车辆随机到达一个路口，遇到红灯 C、射击运动员射击一次，击中靶心 D、掷一枚质地均匀的骰子，掷出的点数是质数

查看试题解析
5. 下列运算正确的是（　　）

A、x⁸÷x²=x⁶ B、（x³y）²=x⁵y² C、﹣2（a﹣1）=﹣2a+1 D、（x+3）²=x²+9

查看试题解析
6. 下列命题：①相等的两个角是对顶角；②若∠1+∠2＝180°，则∠1与∠2互为补角；③同旁内角互补；④垂线段最短，其中假命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图是七年级某考生做的水滴入一个玻璃容器的示意图（滴水速度保持不变），能正确反映容器中水的高度（ $h$ ）与时间（ $t$ ）之间对应关系的大致图象是（）．

A、 B、 C、 D、

查看试题解析
8. 如图，已知AB∥CD，CE，AE分别平分∠ACD，∠CAB，则∠1＋∠2的度数为（）

A、90° B、180° C、120° D、150°

查看试题解析
9. 如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO=106°，则∠C的度数为（）

A、40° B、37° C、36° D、32°

查看试题解析
10. 如图，△ABC和△BDE都是等边三角形，点A，B，D在一条直线上。给出4个结论：①AE=CD；②AB⊥FB；③∠AFC=60°；④△BGH是等边三角形。其中正确的是（）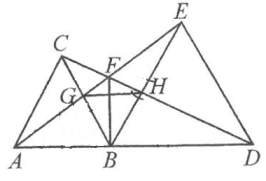

A、①，②，③ B、①，②，④ C、①，③，④ D、②，③，④

查看试题解析

二、填空题（每空3分，共15分）

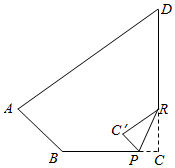
11. 若x²－（m+1）x＋9是—个完全平方式，则m的值为.

查看试题解析
12. 一个等腰三角形一边长为3cm，另一边长为7cm，那么这个等腰三角形的周长cm．

查看试题解析
13. 某鱼塘养了200条鲤鱼、150条鲢鱼和若干条草鱼，通过多次捕捞试验后发现，捕捞到草鱼的频率稳定在0.5左右．若随机在鱼塘中捕捞一条鱼，则捞到鲤鱼的概率为．

查看试题解析
14. 如图，已知四边形纸片ABCD，其中∠B＝120°，∠D＝54°，现将其右下角向内折出△PC′R，恰使C′P∥AB，RC′∥AD，则∠C的度数是.

查看试题解析
15. 如图，已知方格纸中是 4 个相同的正方形，则∠1 与∠2 的度数和为.

查看试题解析

三、计算题（共2题，共14分）

16. 用简便算法计算：

(1)、 $60 0^{2} - 603 \times 597$

(2)、 $10 4^{2}$

查看试题解析
17.

(1)、化简： $(3 x^{2} y^{2} + 4 x^{3} y - 4 x^{2} y) \div x y - (2 x - 1)^{2}$ ．

(2)、先化简，再求值： $(2 x + y)^{2} - 4 x (x + 2 y) - 3 y^{2}$ ，其中 $x = - 4$ ， $y = \frac{1}{2}$ ．

查看试题解析

四、解答题（共5题，共41分）

18. 如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.

(1)、在图中作出△ABC关于直线l对称的△A₁B₁C₁；（要求：A与A₁ ， B与B₁ ， C与C₁相对应）

(2)、在（1）问的结果下，连接BB₁ ， CC₁ ，求四边形BB₁C₁C的面积.

查看试题解析
19. 如图 $A D / / B E ， ∠ E D C = ∠ C$ ，试说明 $∠ A = ∠ E$ ．

查看试题解析
20. 为了了解某种车的耗油量，我们对这种车在高速公路上做了耗油实验，并把实验的数据记录下来，制成下表：
汽车行驶时间x（h）
0
1
2
3
…
邮箱剩余油量y（L）
100
94
88
82
…

(1)、根据上表的数据，请写出y与x的之间的关系式：；

(2)、如果汽车油箱中剩余油量为46L，则汽车行驶了多少小时？

(3)、如果该种汽车油箱只装了36L汽油，汽车以100km/h的速度在一条全长700公里的高速公路上均匀行驶，请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗？为什么？

查看试题解析
21.

(1)、如图，在△ABC中，AB＝AC，点E，F分别在AB，AC上，AE＝AF，BF与CE相交于点P.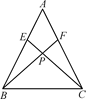
求证：PB＝PC.

(2)、补充完成下列推理过程：
如图，在△ABC中，AB＝AC，点D，E分别是BC，AC上的点，且BD＝CE，连接AD，DE，若∠ADE＝∠B.
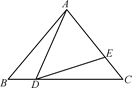
求证：AD＝DE.
证明：∵AB＝AC，∴∠B＝∠C(▲ )．
∵∠ADC＝∠B＋∠_▲_ (_▲)，且∠ADE＝∠B，
∴∠ADC＝∠ADE＋∠_▲_．又∵∠ADC＝∠ADE＋∠CDE，∴∠BAD＝∠CDE.
在△BAD和△CDE中，
${\begin{matrix} \begin{array}{l} ∠ B = ∠ C \\ ∠ B A D = ∠ C D E \end{array} \\ B D = C E \end{matrix}$ ∴△BAD≌△CDE(__▲)．∴AD＝DE(_▲)．

查看试题解析
22. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为a的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．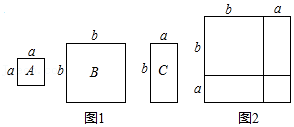

(1)、请用两种不同的方法求图2大正方形的面积：
方法1：；方法2：；

(2)、观察图2，请你写出代数式：（a+b）² ， a²+b² ， ab之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：
①已知：a+b＝5，（a-b）²＝13，求ab的值；

②已知（2023-a）²+（a-2022）²＝5，求（2023-a）（a-2022）的值．

查看试题解析

汽车行驶时间x（h）	0	1	2	3	…
邮箱剩余油量y（L）	100	94	88	82	…