2023年北师大版数学七年级下学期期末模拟试卷（1）

试卷更新日期：2023-05-28 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 计算t⁶•t²的结果是（）

A、t⁴ B、t⁸ C、2t⁸ D、t¹²

查看试题解析
2. 下列是北京大学，中国科学院，中国医科大学和中国人民公安大学的标志中的图案，其中是轴对称图形的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 某种原子的直径为0.0000000002米，数据0.0000000002用科学记数法表示为（）．

A、 $0.2 \times 1 0^{- 10}$ B、 $1 \times 1 0^{- 10}$ C、 $2 \times 1 0^{- 10}$ D、 $0.1 \times 1 0^{- 10}$

查看试题解析
4. 下列运算一定正确的是（）

A、 $x + x^{2} = x^{3}$ B、 $2 x^{3} \div x^{2} = x$ C、 $x^{3} \cdot x^{2} = x^{5}$ D、 ${(\frac{x}{2})}^{3} = \frac{x^{3}}{2}$

查看试题解析
5. 下列计算正确的是（）

A、 $3 b^{4} \cdot 2 b^{4} = 6 b^{4}$ B、 $5 a^{5} \cdot 3 a^{3} = 15 a^{15}$ C、 $3 a^{2} + 4 a^{2} = 7 a^{4}$ D、 $3 a^{9} \div 2 a^{9} = \frac{3}{2}$

查看试题解析
6. 以下列各组线段的长为边，能组成三角形的是（）

A、2、4、7 B、3、5、2 C、7、5、3 D、9、5、3

查看试题解析
7. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字外其他均相同，将它们背面朝上，从中任抽一张，抽到负数的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{2}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
8. 如图，点B、E、C、F四点共线，∠B ＝∠DEF，BE ＝ CF，添加一个条件，不能判定 △ABC ≌ △DEF的是（）

A、∠A＝∠D B、AB＝DE C、AC∥DF D、AC＝DF

查看试题解析
9. 下列说法正确的是（）

A、两个面积相等的图形一定是全等图形 B、两个全等图形形状一定相同 C、两个周长相等的图形一定是全等图形 D、两个正三角形一定是全等图形

查看试题解析
10. 如图所示，在△ABC中，点M，N分别是边AB，BC上的点，将△BNM沿MN折叠，使点B落在点B'处．若∠B=35°，∠BNM=28°，则∠AMB'的度数为（）．

A、30° B、37° C、54° D、63°

查看试题解析

二、填空题（每空3分，共15分）

11. 已知 $2^{m} = 7$ ， $2^{n} = 5$ ，则 $2^{m - n} =$ ．

查看试题解析
12. 一只蚂蚁自由自在地在用七巧板拼成的正方形中爬来爬去（每块七巧板的表面完全相同），它最终停留在1号七巧板上的概率．

查看试题解析
13. 如图所示，直线a∥b，三角板的直角顶点放在直线b上．若∠1=65°，则∠2= ．

查看试题解析
14. 若a+b=4，ab=3，则(a-b)²＝．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C = 5$ ， $A D$ 是 $△ A B C$ 的一条角平分线，点 $E$ ，点 $F$ 分别是线段 $A D$ ， $A C$ 上一动点，若 $A D = 4$ ， $B D = 3$ ，那么线段 $C E + E F$ 的最小值是．

查看试题解析

三、计算题（共2题，共13分）

16. 计算：

(1)、 (π-3)⁰+( $\frac{1}{2}$ )^-2+(-1)²⁰²²；

(2)、x·x²·x³+(x²)³-2(x³)²；

(3)、 (a+3b-2c)(a+3b+2c)；

(4)、 2022²-2021×2023．

查看试题解析
17. 已知 $m^{2} - 2 m n - 1 = 0$ ，求代数式 ${(m - n)}^{2} + (m + n) (m - n) - m^{2}$ 的值．

查看试题解析

四、解答题（共5题，共42分）

18. 如图，现有一个转盘被平均分成6等份，分别标有数字2，3，4，5，6，7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字，

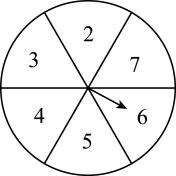(1)、转到数字10是（从“随机事件”“必然事件”“不可能事件”中选一个填入）；

(2)、转动转盘，转出的数字是2的倍数比转出的数字是3的倍数的可能性（从“大”“小”“相等”中选一个填入）；

(3)、转动转盘，转出的数字大于3的概率是；

(4)、现有一张写有数字5的卡片，要随机转动转盘，转盘停止后记下转出的数字，与卡片上的数字和为奇数的概率是．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ．

(1)、利用尺规，作 $A B$ 边的垂直平分线交 $A C$ 于点 $D$ ，交 $A B$ 于点 $E$ ；（不写作法，保留作图痕迹）

(2)、在（1）中，连接 $B D$ ，若 $∠ D B C = 27 °$ ，试求出 $∠ A$ 的度数．

查看试题解析
20. 从边长为 $a$ 的正方形减掉一个边长为 $b$ 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．

(1)、上述过程所揭示的乘法公式是．

(2)、若 $9 x^{2} - 16 y^{2} = 30$ ， $3 x + 4 y = 6$ ，求 $3 x - 4 y$ 的值．

(3)、计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \cdot \cdot \cdot (1 - \frac{1}{9 9^{2}}) (1 - \frac{1}{10 0^{2}})$ ．

查看试题解析
21. 疫情期间，全民检测，人人有责，幸福小区某时段进行核酸检测，居民有序排队入场，医务人员开始检测后，现场排队等待检测人数 $y$ （人）与时间 $x$ （分钟）之间的关系式为 $y = 10 x + a$ ，用表格表示为：
时间 $x$ /分钟
0
1
2
3
4
5
6
…
等待检测人数 $y$ /人
40
50
60
70
80
90
100
医务人员已检测的总人数（人）与时间（分钟）之间的关系如图所示：

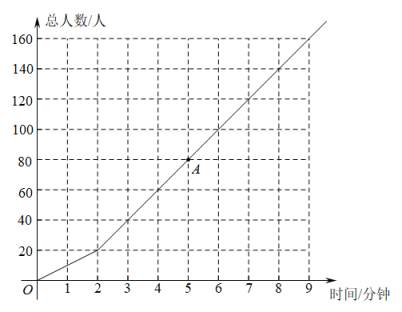(1)、图中表示的自变量是，因变量是；

(2)、图中点 $A$ 表示的含义是；

(3)、在医务人员开始检测4分钟时，现场排队等待检测的人数有人；

(4)、关系式 $y = 10 x + a$ 中， $a$ 的值为；

(5)、医务人员开始检测分钟后，现场排队等待检测人数与医务人员已检测的总人数相同；

(6)、如果该小区共有居民1200人，那么医务人员全部检测完该小区居民共需分钟．

查看试题解析
22. 如图， $∠ B A D = ∠ C A E = 90 °$ ， $A B = A D$ ， $A E = A C$ ， $A F ⊥ C B$ ，垂足为 $F$ ．

(1)、求证： $△ A B C ≌ △ A D E$ ；

(2)、求 $∠ F A E$ 的度数；

(3)、请直接写出 $C D$ ， $B F$ ， $D E$ 三者的数量关系为：．

查看试题解析

时间 $x$ /分钟	0	1	2	3	4	5	6	…
等待检测人数 $y$ /人	40	50	60	70	80	90	100