2023年浙教版数学八年级下学期高分速效复习12 反比例函数(提高版)
试卷更新日期:2023-05-28 类型:复习试卷
一、单选题(每题2分,共20分)
-
1. 给出下列函数关系式:①;②;③;④;⑤2xy=1;⑥-xy=2.其中,表示y是x的反比例函数的个数为( )A、3 B、4 C、5 D、62. 如图,点是反比例函数图象第二象限上的两点,射线交轴于点 , 且恰好为中点,过点作轴的平行线,交射线于点 , 若的面积为 , 则的值为( )
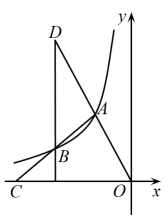 A、-6 B、-4 C、-8 D、-103. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( )
A、-6 B、-4 C、-8 D、-103. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( ) A、-8 B、-6 C、-4 D、-25. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( )
A、-8 B、-6 C、-4 D、-25. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( ) A、 B、 C、 D、6. 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
A、 B、 C、 D、6. 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
①双曲线的解析式为y=(x>0);②点E的坐标是(4,8);③sin∠COA=;④AC+OB=12 .
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个7. 如图,A、B是双曲线y=上的两点,经过A、B两点分别作AC∥y轴,BC∥x轴两线交于点C,已知S△AOC=3,S△ABC=9,则k的值为( ) A、12 B、10 C、8 D、48. 如图,直线与轴交于点 , 与轴交于点 , 以为边作矩形ABCD,点在轴上.双曲线经过点 , 与直线交于点 , 则点的坐标为( )
A、12 B、10 C、8 D、48. 如图,直线与轴交于点 , 与轴交于点 , 以为边作矩形ABCD,点在轴上.双曲线经过点 , 与直线交于点 , 则点的坐标为( ) A、 B、 C、 D、9. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( )
A、 B、 C、 D、9. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、410. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A、1 B、 C、2 D、410. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( ) A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是
A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是二、填空题(每空2分,共12分)
-
11. 已知y与2z成反比例,比例系数为k1 , z与 x成正比例,比例系数为k2 , k1和k2是已知数,且k1•k2≠0,则y关于x成 比例.(填“正”或“反”)12. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
 13. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .
13. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .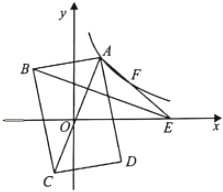 14. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=.
14. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=. 15. 为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量与燃烧时间x(分)成正比例;燃烧后,y与x成反比例.若 , 则x的取值范围是.
15. 为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量与燃烧时间x(分)成正比例;燃烧后,y与x成反比例.若 , 则x的取值范围是. 16. 已知双曲线与函数的图像有两个交点,则a的值是.
16. 已知双曲线与函数的图像有两个交点,则a的值是.三、综合题
-
17. 已知函数 .(1)、当 为何值时,此函数是反比例函数?(2)、当 为何值时,此函数是正比例函数?18. 某市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为 的条件下生长最快的新品种,下图是某天恒温系统从开启到关闭及关闭后,大棚里温度 随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线 的一部分,请根据图中信息解答下列问题.
 (1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?19. 如图,平行四边形OABC的边OA在x轴的正半轴上, , , CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E.
(1)、恒温系统在这天保持大棚内温度为 的时间有多少小时?(2)、求 的值.(3)、恒温系统在一天24h内保持大棚温度在 的时间有多少小时?19. 如图,平行四边形OABC的边OA在x轴的正半轴上, , , CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E. (1)、求k的值及直线CD的解析式;(2)、求证:;(3)、求点E的坐标.20. 如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.
(1)、求k的值及直线CD的解析式;(2)、求证:;(3)、求点E的坐标.20. 如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.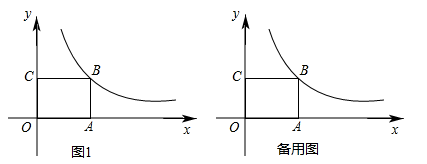 (1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.21. 综合与探究
(1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.21. 综合与探究如图1,反比例函数的图象经过点A,点A的横坐标是-2,点A关于坐标原点O的对称点为点B,作直线 .
 (1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.22. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)、判断点B是否在反比例函数的图象上,并说明理由;(2)、如图1,过坐标原点O作直线交反比例函数的图象于点C和点D,点C的横坐标是4,顺次连接 , , 和 . 求证:四边形是矩形;(3)、已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.22. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整: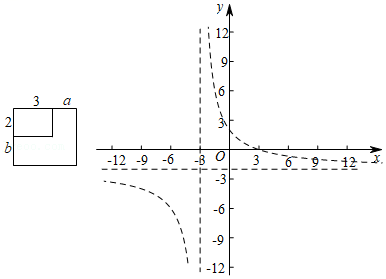 (1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:
(1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:①求出方程|﹣2|=0的根;
②如果方程|﹣2|=a有2个实数根,请直接写出a的取值范围.
23. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 并与反比例函数的图象在第一象限相交于点 , 且点是的中点. (1)、如图1,求反比例函数的解析式;(2)、如图2,若矩形的顶点在直线上,顶点在点右侧的反比例函数图象上,顶点 , 在轴上,且 .
(1)、如图1,求反比例函数的解析式;(2)、如图2,若矩形的顶点在直线上,顶点在点右侧的反比例函数图象上,顶点 , 在轴上,且 .①求点的坐标;
②若点是反比例函数的图象第一象限上的动点,且在点的左侧,连结 , 并在左侧作正方形当顶点或顶点恰好落在直线上,直接写出对应的点的横坐标.
24. 如图,点A,点B是直线y=x+2上的两动点,点A在点B左侧,且 , 反比例函数与分别过点A、点B. (1)、若A的坐标为 , 求和的值.(2)、点A的横坐标记为a,当a=0时我们发现,点A落在y轴上,反比例函数不存在,所以.参照上述过程,请直接写出a不能取的其他值.(3)、若 , 求点A的坐标.
(1)、若A的坐标为 , 求和的值.(2)、点A的横坐标记为a,当a=0时我们发现,点A落在y轴上,反比例函数不存在,所以.参照上述过程,请直接写出a不能取的其他值.(3)、若 , 求点A的坐标.