2023年浙教版数学八年级下学期高分速效复习10 特殊平行四边形（提高版）

试卷更新日期：2023-05-28 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，矩形 $A B C D$ 中， $A B = 8$ ， $B C = 4$ ，点E，F，G，H分别在矩形 $A B C D$ 各边上，且四边形 $E F G H$ 为平行四边形，则平行四边形 $E F G H$ 周长的最小值为（）

A、 $4 \sqrt{5}$ B、 $8 \sqrt{5}$ C、 $4 \sqrt{3}$ D、 $8 \sqrt{3}$

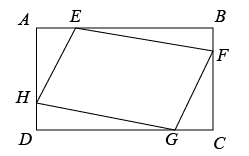查看试题解析
2. 如图，两个全等的矩形AEFG，矩形ABCD如图所示放置．CD所在直线与AE，GF分别交于点H，M．若AB＝3，BC＝ $\sqrt{3}$ ，CH＝MH．则线段MH的长度是（）

A、 $\frac{3}{2}$ B、 $\sqrt{6}$ C、 $\sqrt{3}$ D、2

查看试题解析
3. 如图，一块长方形场地 $ABCD$ 的长 $AB$ 与宽 $BC$ 的比是 $\sqrt{2}$ ： $1$ ， $DE ⊥ AC$ ， $BF ⊥ AC$ ，垂足分别是 $E$ 、 $F$ 两点.现计划在四边形 $DEBF$ 区域种植花草，则四边形 $DEBF$ 与长方形 $ABCD$ 的面积比等于（）

A、1：3 B、2：3 C、1：2 D、1：4

查看试题解析
4. 如图，菱形ABCD中∠ABC＝60°，ΔABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的个数是（）
①△AMB ≌△ENB；②若菱形ABCD的边长为2，则AM＋CM的最小值2；③连接AN，则AN⊥BE；④当AM＋BM＋CM的最小值为 $4 \sqrt{3}$ 时，菱形ABCD的面积也为 $4 \sqrt{3}$ .

A、1 B、2 C、3 D、4

查看试题解析
5. 将2021个形状、大小均相同的菱形按照如图所示的方式排成一列，使得右侧菱形的顶点与左侧菱形的对角线交点重合，若这些菱形的边长均为2，则阴影部分的周长总和等于（）

A、 $4042$ B、 $8076$ C、 $8080$ D、 $8084$

查看试题解析
6. 如图，由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案，其重叠部分是正八边形(阴影部分)，点B，D在EG上，点F，H在AC上，若CF=2，则BD的长为（）

A、4 B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、2 $\sqrt{5}$

查看试题解析
7. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4.$ 分别以 $A B$ 、 $A C$ 、 $B C$ 为边在 $A B$ 的同侧作正方形 $A B E F$ 、 $A C P Q$ 、 $B C M N$ ，四块阴影部分的面积分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 、 $S_{4} .$ 则 $S_{1} - S_{2} + S_{3} + S_{4}$ 等于（）

A、4 B、6 C、8 D、12

查看试题解析
8. 如图，在平面直角坐标系 $x O y$ 中，正方形 $A B C D$ 的顶点 $A (1 ， - 1)$ ， $D (3 ， - 1)$ ，规定把正方形 $A B C D$ “先沿 $y$ 轴翻折，再向下平移1个单位”为一次变换，这样连续经过2022次变换后，点 $C$ 的坐标为（）

A、 $(- 3 ， - 2023)$ B、 $(3 ， - 2024)$ C、 $(3 ， - 2025)$ D、 $(- 3 ， - 2026)$

查看试题解析
9. 如图，正方形 $A B C D$ 中，点P为 $B D$ 延长线上任一点，连结 $P A$ ，过点P作 $P E ⊥ P A$ ，交 $B C$ 的延长线于点E，过点E作 $E F ⊥ B P$ 于点F.下列结论：① $P A = P E$ ；② $B D = 2 P F$ ；③ $C E = \sqrt{2} P D$ ；④若 $B P = B E$ ，则 $P F = (\sqrt{2} + 1) D F$ .其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示．连结CF，并延长交AB于点N．若AB＝3 $\sqrt{5}$ ， EF＝3，则FN的长为（）

A、2 B、 $\sqrt{5}$ C、 $2 \sqrt{2}$ D、3

查看试题解析

二、填空题（每空4分，共28分

11. 如图1是第32届夏季奥运会的会徽，它是由三种不同规格的全等矩形组成，代表了不同的国家、文化和思维方式，表达了多样性的融合．图2和图3为该会徽中的某一部分。如图2，三种矩形分别由三种不同的菱形依次连结各边中点得到，其中∠AOC=120°，∠AOB=90°．如图3，点D恰好在FE的延长线上，则∠IHE= 度．若AO=1，则点F，G之间的距离为

查看试题解析
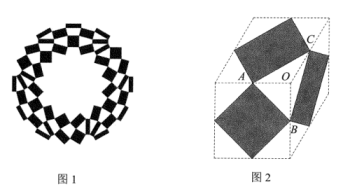
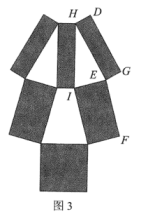12. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 2 \sqrt{5}$ ， $A C = \sqrt{5}$ ，点 $D$ 在 $A B$ 上， $A D = 1$ ，现将一个足够大的三角板的直角顶点与点 $D$ 重合，并绕着点 $D$ 转动，三角板的两直角边分别与 $A C$ 、 $B C$ 交于点 $E$ 、 $F$ ，连结 $E F$ ，以 $E D$ 、 $E F$ 为邻边作平行四边形 $D E F G$ ，在转动过程中，当线段 $E F$ 的长度最小时，平行四边形 $D E F G$ 的面积为.

查看试题解析
13. 已知，菱形ABCD（∠C＜90°）的对角线长分别为6和8，点E在边BC上，BE＝1，若点F在直线AB上，且AE＝DF，则BF的长为.

查看试题解析
14. 如图，直线 $y = - \frac{3}{4} x + 3$ 与x轴、y轴分别交于点A，B，M是x轴上一点（不与点A重合），N是平面直角坐标系中第一象限内任意一点.若以A，B，M，N为顶点的四边形是菱形，则满足条件的点M的坐标是.

查看试题解析
15. 如图，点E，F，G，H为正方形 $A B C D$ 四边中点，连接 $B E$ ， $D G$ ， $C F$ ， $A H$ .若 $A B = 10$ ，则四边形 $M N P Q$ 的面积是.

查看试题解析
16. 如图，正方形ABCD边长为2，F为对角线AC上的一个动点，过C作AC的垂线并截取 $C E = A F$ ，连结EF， $△ E C F$ 周长的最小值为．

查看试题解析

三、作图题（共12分）

17. 如图，在正方形ABCD中，点E为边AD中点. 用无刻度直尺画出以下图形，画图过程用虚线表示，画图结果用实线表示．

(1)、在边BC上找点F使直线EF平分正方形ABCD的面积；

(2)、画出边AB的中点N；

(3)、在边CD上找点Q使AQ⊥BE；

(4)、在直线BC上找点P使DP // CE．

查看试题解析

四、解答题（共7题，共80分）

18. 我们定义：只有一组对角相等的凸四边形叫做等对角四边形．

(1)、四边形ABCD是等对角四边形， $∠$ A≠ $∠$ C，若 $∠$ A＝50°， $∠$ B＝100°，则 $∠$ C＝， $∠$ D＝．

(2)、图①、图②均为4×4的正方形网格，线段AB、BC的端点均在格点上，按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD．要求：四边形ABCD的顶点D在格点上，且两个四边形不全等．

(3)、如图③，在平行四边形ABCD中， $∠$ A＝60°，AB＝12，AD＝6，点E为AB的中点，过点E作EF $⊥$ DC，交DC于点F．点P是射线FE上一个动点，设FP＝x，求以点A、D、E、P为顶点的四边形为等对角四边形时x的值．

查看试题解析
19. 如图，在长方形 $ABCD$ 中，边 $AB$ 、 $BC$ 的长 $(AB < BC)$ 是方程 $x^{2} - 7 x + 12 = 0$ 的两个根.点 $P$ 从点 $A$ 出发，以每秒 $1$ 个单位的速度沿 $△ ABC$ 边 $A \to B \to C \to A$ 的方向运动，运动时间为 $t ($ 秒 $)$ .

(1)、求 $AB$ 与 $BC$ 的长；

(2)、当点 $P$ 运动到边 $BC$ 上时，试求出使 $AP$ 长为 $\sqrt{10}$ 时运动时间 $t$ 的值；

(3)、当点 $P$ 运动到边 $AC$ 上时，是否存在点 $P$ ，使 $△ CDP$ 是等腰三角形？若存在，请求出运动时间 $t$ 的值；若不存在，请说明理由.

查看试题解析
20. 已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．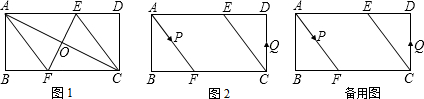

(1)、如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

(2)、如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．

查看试题解析
21. 问题：如图，在 $▱ A B C D$ 中， $A B = 8$ ， $A D = 5$ ， $∠ D A B$ ， $∠ A B C$ 的平分线AE，BF分别与直线CD交于点E，F，求EF的长.
答案： $E F = 2$ .
探究：

(1)、把“问题”中的条件“ $A B = 8$ ”去掉，其余条件不变.
①当点E与点F重合时，求AB的长；
②当点E与点C重合时，求EF的长.

(2)、把“问题”中的条件“ $A B = 8$ ， $A D = 5$ ”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求 $\frac{A D}{A B}$ 的值.

查看试题解析
22. 如图1，矩形ABCD中，过对角线AC的中点O画EF⊥AC分别交AB，CD于点E，F，连结AF，CE．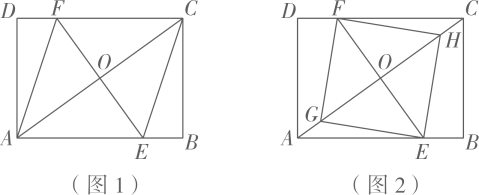

(1)、[证明体验]
求证：四边形AECF是菱形．

(2)、[基础巩固]
若AB=8，BC=6，求菱形AECF的边长．

(3)、[拓展延伸]
如图2，在对角线AC上取点G，H，使得四边形EHFG是正方形，若正方形EHFG的边长为 $3 \sqrt{2}$ ，且AE=5CH，求矩形ABCD的面积．

查看试题解析
23. 已知，如图：在直角坐标系中，正方形AOBC的边长为4，点D，E分别是线段AO，BO上的动点，D点由A点向O点运动，速度为每秒1个单位，E点由B点向O点运动，速度为每秒2个单位，当一个点停上运动时，另一个点也随之停止，设运动时间为t（秒）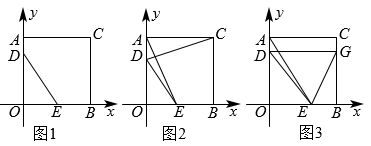

(1)、如图1，当t为何值时，△DOE的面积为6；

(2)、如图2，连接CD，与AE交于一点，当t为何值时，CD⊥AE；

(3)、如图3，过点D作DG $∥$ OB，交BC于点G，连接EG，当D，E在运动过程中，使得点D，E，G三点构成等腰三角形，求出此时t的值.

查看试题解析
24. 若一个四边形有一组邻边相等，且这组邻边夹角所对的对角线平分一个内角，则称这样的四边形为“近似菱形”．例如：如图1，在四边形ABCD中，AB＝AD，BD平分∠ABC，则四边形ABCD是近似菱形．

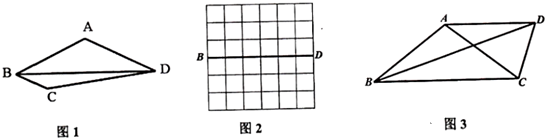(1)、请在图2中作出一个以BD为对角线的“近似菱形”ABCD，顶点A、顶点C要在网格格点上．

(2)、如图3，在四边形ABCD中，AB＝AC，AD∥BC，∠CAD＝2∠DBC．求证：四边形ABCD是“近似菱形”．

(3)、在（2）的条件下，若BD＝3，CD＝1，求AB的长．

查看试题解析