2023年浙教版数学七年级下学期高分速效复习10 分式（提高版）

试卷更新日期：2023-05-28 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知三个数 $a ， b ， c$ 满足 $\frac{a b}{a + b} = \frac{1}{5}$ ， $\frac{b c}{b + c} = \frac{1}{6}$ ， $\frac{c a}{c + a} = \frac{1}{7}$ ，则 $\frac{a b c}{a b + b c + c a}$ 的值是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{15}$ D、 $\frac{1}{20}$

查看试题解析
2. 若 $a$ ， $b$ 为实数且满足 $a \neq - 1$ ， $b \neq - 1$ ，设 $M = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $N = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，有以下2个结论： $①$ 若 $a b = l$ ，则 $M = N$ ； $②$ 若 $a + b = 0$ ，则 $M N \leq 0 .$ 下列判断正确的是（）

A、①对②错 B、①错②对 C、①②都错 D、①②都对

查看试题解析
3. 商家常将单价不同的A，B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A，B两种糖的总价与A，B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A种糖的单价为（）

A、50元/千克 B、60元/千克 C、70元/千克 D、80元/千克

查看试题解析
4. 已知分式 $\frac{5 x + n}{x - m}$ （m，n为常数）满足下列表格中的信息：则下列结论中错误的是（）

x的取值

－2

2

p

q

分式的值

无意义

2

0

1

A、m＝－2 B、n＝－2 C、 $p = \frac{2}{5}$ D、q＝－1

查看试题解析
5. 对于分式中四个符号，任意改变其中两个符号，分式的值不变是（）

A、①③ B、①② C、②③ D、②④

查看试题解析
6. 已知 $a > 1$ ， $A = \frac{a}{a - 1}$ ， $B = \frac{a - 1}{a}$ ， $C = \frac{a}{a + 1}$ ，则 $A$ 、 $B$ 、 $C$ 的大小关系是（）

A、 $A > C > B$ B、 $A > B > C$ C、 $C > B > A$ D、 $C > A > B$

查看试题解析
7. 已知实数a，b，c满足 $a + b = a b = c$ ，有下列结论： $①$ 若 $c = 5$ ，则 $a^{2} + b^{2} = 15$ ； $②$ 若 $a = 3$ ，则 $b + c = 9$ ； $③$ 若 $c \neq 0$ ，则 $\frac{a - 3 a b + b}{2 a + 7 a b + 2 b} = - \frac{2}{9}$ ； $④$ 若 $c \neq 0$ ，则 $(1 - a) (1 - b) = \frac{1}{a} + \frac{1}{b}$ ，其中结论正确的有（）

A、 $① ③$ B、 $① ② ④$ C、 $① ② ③$ D、 $① ③ ④$

查看试题解析
8. 已知关于x的分式 $\frac{x - a}{x - 2} + \frac{2 a}{2 - x} = 2$ 的解为非负数，则a的范围为（）

A、 $a \leq \frac{4}{3}$ 且 $a \neq \frac{2}{3}$ B、 $a \geq \frac{2}{3}$ 且 $a \neq \frac{4}{3}$ C、 $a \leq - \frac{1}{3}$ 且 $a \neq - \frac{2}{3}$ D、 $a \geq \frac{1}{3}$ 且 $a \neq \frac{2}{3}$

查看试题解析
9. 甲、乙、丙三名工人共承担装搭一批零件.已知甲乙丙丁四人聊天时的对话信息如下：
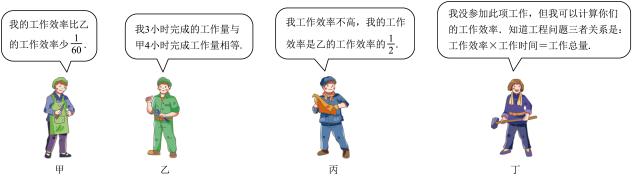
如果每小时只安排1名工人，那么按照甲、乙、丙的轮流顺序至完成工作任务，共需（）小时.

A、20 B、21 C、19 $\frac{1}{4}$ D、19 $\frac{3}{4}$

查看试题解析

10. 2021年5月1日，浙江省正式实施《浙江省生活垃圾管理条例》，生活垃圾按照厨余垃圾、可回收物、有害垃圾、其他垃圾进行分类.贝贝所住小区5月和12月的厨余垃圾分出量和其他三种垃圾的总量的相关信息如下表所示：

月份

类别

5月

12月

厨余垃圾分出量(千克)

600

8400

其他三种垃圾的总量(千克)

$\frac{7}{10} x$

如果厨余垃圾分出率= $\frac{厨余垃圾分出量}{生活垃圾总量} \times 100 %$ ，(生活垃圾总量=厨余垃圾分出量+其他三种垃圾的总量)，且该小区12月的厨余垃圾分出率约是5月的厨余垃圾分出率的14倍，那么下面列式正确的是（）

A、

\frac{660}{x} \times 14 = \frac{8400}{\frac{7}{10} x}

B、

\frac{660}{660 + x} \times 14 = \frac{8400}{8400 + \frac{7}{10} x}

C、

\frac{660}{660 + x} = \frac{8400}{8400 + \frac{7}{10} x} \times 14

D、

\frac{660 + x}{660} \times 14 = \frac{8400 + \frac{7}{10} x}{8400}

查看试题解析

二、填空题（每空3分，共18分

11. 某段高速公路全长280公里，交警部门在高速公路上距入口3千米处设立了限速标志牌，并在以后每隔5公里处设置一块限速标志牌；此外交警部门还在距离入口10千米处设置了摄像头，并在以后每隔16千米处都设置一个摄像头（如图），则在此段高速公路上，离入口千米处刚好同时设置有标志牌和摄像头．

查看试题解析
12. 如图，在长方形ABCD中，AB=10，BC=13．E，F，G，H分别是线段AB，BC，CD，AD上的定点．现分别以BE，BF为边作长方形BEQF，以DG为边作正方形DGIH．若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且BE=DG，Q，I均在长方形ABCD内部．记图中的阴影部分面积分别为S₁ ， S₂ ， S₃ ．若 $\frac{S_{2}}{S_{1}} = \frac{3}{7}$ ，则S₃= ．

查看试题解析
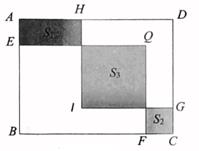13. 从下列几个均不为零的式子 $x^{2} - 4 ， x^{2} - 2 x ， x^{2} - 4 x$ $+ 4 ， x^{2} + 2 x ， x^{2} + 4 x + 4$ 中任选两个都可以组成分式，请选择一个不是最简分式的分式进行化简：

查看试题解析
14. 若代数式 $\frac{x^{2} - 3 x - 2}{x - 3}$ 表示一个自然数，则符合条件的整数 $x$ 的个数为.

查看试题解析
15. 若 $\frac{1}{x} + \frac{2}{y} + \frac{3}{z} = 5$ ， $\frac{3}{x} + \frac{2}{y} + \frac{1}{z} = 7$ ，则 $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} =$ .

查看试题解析
16. 将 $f = \frac{u v}{u + v}$ 变形为已知f，u，且 $f \neq u$ ，则 $v$ 的公式为.

查看试题解析

三、解答题（共6题，共48分）

17. 用如图所示的甲、乙、丙三块木板做一个长、宽、高分别为a厘米，b厘米和10厘米的长方体木箱，其中甲块木板锯成两块刚好能做箱底和一个长侧面，乙块木板刚好能做一个长侧面和一个短侧面，丙块木板刚好能做一个箱盖和剩下的一个短侧面（厚度忽略不计，a＞b）

(1)、用含a，b的代数式分别表示这三块木板的面积.

(2)、若甲块木板的面积比丙块木板的面积大200平方厘米，木箱的体积为150000立方厘米，求乙块木板的面积.

(3)、如果购买一块长为100厘米，宽为（a+b）厘米的长方形木板做这个木箱，木板的利用率为90%，试求分式 $\frac{5}{a} + \frac{5}{b}$ + $\frac{a^{2} b - a b^{2}}{7 a^{2} - 7 b^{2}}$ 的值.

查看试题解析
18. 【学习材料】——拆项添项法
在对某些多项式进行因式分解时，需要把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符号相反的项，这样的分解因式的方法称为拆项添项法，如：
例1分解因式： $x^{4} + 4$

(1)、运用拆项添项法分解因式： $x^{4} + 4 y^{4}$ .

(2)、化简： $\frac{x^{3} - x^{2} - 4}{x - 2}$ .

查看试题解析
19. 阅读下面材料，解答问题.
解方程： $\frac{x - 1}{x} - \frac{4 x}{x - 1} = 0$ .

解：设 $y = \frac{x - 1}{x}$ ，则原方程化为 $y - \frac{4}{y} = 0$ .

方程两边同时乘 $y$ ，得 $y^{2} - 4 = 0$ ，

解得 $y = \pm 2$ .

经检验 $y = \pm 2$ 都是方程 $y - \frac{4}{y} = 0$ 的根.

∴当 $y = 2$ 时， $\frac{x - 1}{x} = 2$ ，觕得 $x = - 1$ ；

当 $y = - 2$ 时， $\frac{x - 1}{x} = - 2$ ，解得 $x = \frac{1}{3}$ .

经检噞 $x = - 1$ 或 $x = \frac{1}{3}$ 都是原分式方程的偨，

∴原分式堭的根为 $x = - 1$ 或 $x = \frac{1}{3}$ .

上述这种解分式方程的方法称为换元法.问题：

(1)、若在方程 $\frac{x - 1}{4 x} - \frac{x}{x - 1} = 0$ 中，设 $y = \frac{x - 1}{x}$ ，则原为程可化为.

(2)、若在方程 $\frac{x - 1}{x + 1} - \frac{4 x + 4}{x - 1} = 0$ 中，设 $y = \frac{x - 1}{x + 1}$ ，则原方䅜可化为.

(3)、利用上述换元法解方程 $\frac{x - 1}{x + 2} - \frac{3}{x - 1} - 1 = 0$ .

查看试题解析
20. 某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有)，各礼品的数量和批发单价列表如下：

甲
乙
丙
数量(个)
m
$3 m$
$n$
批发单价(元)
$a (1 \leq m \leq 10)$
$b$
$10$
$0.8 a (m > 10)$

(1)、当 $m = 5$ 时，若这三种礼品共批发 $35$ 个，甲礼品的总价不低于丙礼品的总价，求a的最小值．

(2)、已知该店用 $1320$ 元批发了这三种礼品，且 $a = 5 b$ ．
$①$ 当 $m = 25$ 时，若批发这三种礼品的平均单价为 $11$ 元/个，求b的值．
$②$ 当 $7 < m < 20$ 时，若该店批发了 $20$ 个丙礼品，且a为正整数，求a的值．

查看试题解析

21. 在乐清某校的压花拓展课上，甲、乙两位同学每小时能共做7幅作品A，甲、乙同时开始制作，当甲做了28幅作品A时，乙做了21幅．

(1)、求甲、乙每小时各做多少幅作品A．

(2)、学校组织义拍资助西部贫困学生的活动，甲、乙两位同学计划共同完成30幅作品A参与义拍，并同时从13：00开始制作。（不考虑休息时间，每人做完一幅作品后才能做下一幅）．

①若甲完成的数量比乙完成的2倍少6幅，求在几时几分恰好全部完成．

②因义拍实际需要，现增加10幅作品B分配给甲、乙两位同学，并要求尽早完成制作，已知甲、乙每小时分别能做6幅和4幅作品B，请你结合方案评价表直接在表格中写出一种作品A，B的分配数量方案．

作品类型	作品A	作品B
分配给甲的数量
分配给乙的数
方案评价表
方案等级	完成时间	评分
合格	18：26~18：36	1分
良好	18：16~18：26	2分
优秀	18：16前	3分

查看试题解析

22. 阅读下列材料：
【材料1】我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2}$ =1+ $\frac{1}{2}$ 。在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为假分式；当分子的次数小于分母的次数时，我们称之为真分式，如 $\frac{x + 1}{x - 1}$ ， $\frac{x^{2}}{x - 2}$ ，…这样的分式是假分式；如 $\frac{2 x - 1}{x^{2} + x}$ 与 $\frac{5}{3 x^{2} + 2}$ …这样的分式是真分式。类似的，假分式也可以化为整式与真分式的和(差)的形式。

例如：将分式 $\frac{x^{2} + 2 x - 5}{x + 3}$ 化成一个整式与一个真分式的和(差)的形式。

方法1： $\frac{x^{2} + 2 x - 5}{x + 3}$ = $\frac{(x^{2} + 3 x) - x - 5}{x + 3}$ = $\frac{x (x + 3) - (x + 3) - 2}{x + 3}$ =x-1- $\frac{2}{x + 3}$

方法2：由分母为x+3，可设x²+2x-5=(x+3)(x+a)+b(a，b为待确定的系数)

∵(x+3)(x+a)+b=x²+ax+3x+3a+b=x²+(a+3)x+(3a+b)

∴x²+2x-5=x²+(a+3)x+(3a+b)

对于任意x，上述等式均成立，

∴ ${\begin{cases} a + 3 = 2 \\ 3 a + b = - 5 \end{cases}$ ，解得 ${\begin{cases} a = - 1 \\ b = - 2 \end{cases}$

∴x²+2x-5=(x+3)(x-1)-2

∴ $\frac{x^{2} + 2 x - 5}{x + 3}$ = $\frac{(x + 3) (x - 1) - 2}{x + 3}$ = $\frac{(x + 3) (x - 1)}{x + 3} - \frac{2}{x + 3}$ =x-1- $\frac{2}{x + 3}$

这样，分式 $\frac{x^{2} + 2 x - 5}{x + 3}$ 就被化成一个整式与一个真分式的和(差)的形式。

【材料2】对于式子2+ $\frac{3}{1 + x^{2}}$ ，由x²≥0知1+x²的最小值为1，所以 $\frac{3}{1 + x^{2}}$ 的最大值为3，

所以2+ $\frac{3}{1 + x^{2}}$ 的最大值为5。

请根据上述材料，解答下列问题：

(1)、分式 $\frac{2}{x + 2}$ 是分式(填“真”或“假”)。

(2)、把下列假分式化成一个整式与一个真分式的和(差)的形式：
① $\frac{2 x + 3}{x}$ =+。

② $\frac{x^{2} - 3 x + 5}{x - 3}$ =+。

(3)、把分式 $\frac{x^{2} + 2 x - 13}{x - 3}$ 化成一个整式与一个真分式的和(差)的形式，并求x取何整数时，这个分式的值为整数。

(4)、当x的值变化时，求分式 $\frac{2 x^{2} - 4 x + 8}{x^{2} - 2 x + 2}$ 的最大值。

查看试题解析

四、计算题（共4题，共24分）

23. 计算： $(\frac{1}{a + b} + \frac{1}{a - b} - \frac{1}{a^{2} - b^{2}}) \div \frac{1}{a^{2} - b^{2}}$ .

查看试题解析
24. 化简： $(a + \frac{1}{a}) (a - \frac{1}{a}) (a^{2} + \frac{1}{a^{2}}) (a^{4} + \frac{1}{a^{4}})$ . $\frac{1}{a^{16} - 1}$

查看试题解析
25. 化简： $\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} +$ $\frac{1}{(x + 3) (x + 4)}$ .

查看试题解析
26. 解分式方程.

(1)、 $\frac{2}{x + 3} = \frac{5}{x}$ ；

(2)、 $\frac{x}{2 x - 5} - 1 = \frac{5}{5 - 2 x}$ ；

(3)、 $\frac{1}{x - 4} = \frac{4}{x^{2} - 16}$ ；

(4)、 $5 + \frac{88}{x^{2} - 16} = \frac{2 x - 1}{x + 4} - \frac{3 x - 1}{4 - x}$

查看试题解析

	甲	乙	丙
数量(个)	m	$3 m$	$n$
批发单价(元)	$a (1 \leq m \leq 10)$	$b$	$10$
批发单价(元)	$0.8 a (m > 10)$	$b$	$10$

x的取值	－2	2	p	q
分式的值	无意义	2	0	1