浙江省温州市鹿城区2021-2022学年六年级下学期数学期末小升初毕业考测试试卷
试卷更新日期:2023-05-26 类型:小升初真题
一、选择。(每题只有一个正确答案,共10分)
-
1. 北京冬奥会冰壶混双比赛于2022年2月2日开始,2月8日决出冠亚军,一共比赛( )天。A、5 B、6 C、7 D、82. 小温期末复习整理了下面的图和算式,其中画框部分表示0.6的是( )。A、
 B、
B、 C、
C、 D、
D、 3. 小温在计算÷3时,探索了下面几种算法,其中算法错误的是( )。A、 B、2÷(5×3) C、×3÷2 D、4. 小温用数字卡片0、2、5、8摆出了所有的三位数,其中最大的三位数是( )。A、质数 B、奇数 C、5的倍数 D、3的倍数5. 如图,直角三角形的两条直角边分别长3cm和4cm,以它较长的直角边为轴旋转一周形成一个圆锥。这个圆锥的( )。
3. 小温在计算÷3时,探索了下面几种算法,其中算法错误的是( )。A、 B、2÷(5×3) C、×3÷2 D、4. 小温用数字卡片0、2、5、8摆出了所有的三位数,其中最大的三位数是( )。A、质数 B、奇数 C、5的倍数 D、3的倍数5. 如图,直角三角形的两条直角边分别长3cm和4cm,以它较长的直角边为轴旋转一周形成一个圆锥。这个圆锥的( )。 A、高是3cm B、底面半径是4cm C、底面积是π×42cm2 D、体积是×π×32×4cm36. 一杯纯牛奶,小温喝了 , 用温水加满后搅拌均匀,又喝了半杯。涂色部分能表示他喝了多少水的是( )。A、
A、高是3cm B、底面半径是4cm C、底面积是π×42cm2 D、体积是×π×32×4cm36. 一杯纯牛奶,小温喝了 , 用温水加满后搅拌均匀,又喝了半杯。涂色部分能表示他喝了多少水的是( )。A、 B、
B、 C、
C、 D、
D、 7. 下面各组中的两种量成正比例关系的是( )。A、小温看一本300页的书,平均每天看的页数与天数。 B、冰墩墩的单价一定,总价与数量。 C、冬奥雪裯运动的路程一定,滑行的速度与时间。 D、新能源汽车的电量一定,消耗的电和剩余电量。8. 一件衣服标价298元出售,现换季促销,降价至198元出售,但仍可赚20%。那么下面算式中表示这件衣服成本的是( )。A、198×(1-20%) B、198×(1+20%) C、198÷(1+20%) D、198÷20%9. 如图,一只蚂蚁从O点出发,沿着半圆的边缘爬了一周,又回到O点,下面可以描述蚂蚁与O点距离变化的是( )。
7. 下面各组中的两种量成正比例关系的是( )。A、小温看一本300页的书,平均每天看的页数与天数。 B、冰墩墩的单价一定,总价与数量。 C、冬奥雪裯运动的路程一定,滑行的速度与时间。 D、新能源汽车的电量一定,消耗的电和剩余电量。8. 一件衣服标价298元出售,现换季促销,降价至198元出售,但仍可赚20%。那么下面算式中表示这件衣服成本的是( )。A、198×(1-20%) B、198×(1+20%) C、198÷(1+20%) D、198÷20%9. 如图,一只蚂蚁从O点出发,沿着半圆的边缘爬了一周,又回到O点,下面可以描述蚂蚁与O点距离变化的是( )。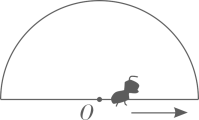 A、
A、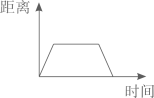 B、
B、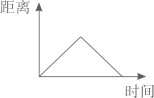 C、
C、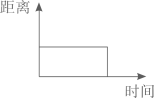 D、
D、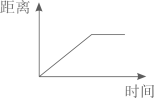 10. 古希腊著名的毕达哥拉斯学派把1,3,6,10,……这样的数称为“三角形数”,而把1,4,9,16,……这样的数称为“正方形数”。
10. 古希腊著名的毕达哥拉斯学派把1,3,6,10,……这样的数称为“三角形数”,而把1,4,9,16,……这样的数称为“正方形数”。
从上图中可以发现:
任何一个大于1的“正方形数"都可以看作两个相邻的“三角形数”之和,例如4=1+3.把“正方形数”36写成两个相邻的“三角形数”之和,正确的是( )。
A、36=10+26 B、36=12+24 C、36=15+21 D、36=16+20二、填空. (每空1分,共23分)
-
11. 据温州市水资源公报显示,2021年平均降水量2228.7mm,折合水量二百六十九亿四千万m3 , 横线上的数写作 , 改写成用“亿”作单位的数是亿m3。12. 在直线上表示出:-2、-0.5、。
 13. =8:=÷=四成= %。14. 一根绳子长5m,先剪去它的 , 又剪去m,还剩下 m。15. 钟面上长度为8cm的分针,经过一小时,它扫过的面积是 cm2 , 它的针尖经过的路程是cm。16. 火箭横型中一个圆柱形零件的高是5mm,在图纸上的高是3cm.这幅图纸的比例尺是。17. 三角形三个内角的度数比是1:3:5,它按角分是三角形,最大角是 °。18. 吃粽子是端午节的一项传统习俗,某店粽子线上和线下销量的比是5:2。如果销售总量是 6300个,那么线上销量是个,线上销量比线下销量多 %。19. 有7个分开摆放的棱长1cm的小正方体,把它们搭成一个几何体(如下图),表面积比原来减少了 cm2。
13. =8:=÷=四成= %。14. 一根绳子长5m,先剪去它的 , 又剪去m,还剩下 m。15. 钟面上长度为8cm的分针,经过一小时,它扫过的面积是 cm2 , 它的针尖经过的路程是cm。16. 火箭横型中一个圆柱形零件的高是5mm,在图纸上的高是3cm.这幅图纸的比例尺是。17. 三角形三个内角的度数比是1:3:5,它按角分是三角形,最大角是 °。18. 吃粽子是端午节的一项传统习俗,某店粽子线上和线下销量的比是5:2。如果销售总量是 6300个,那么线上销量是个,线上销量比线下销量多 %。19. 有7个分开摆放的棱长1cm的小正方体,把它们搭成一个几何体(如下图),表面积比原来减少了 cm2。 20. 神舟十四号载人飞船采用自主快速交会对接模式,当它成功对接于“天和核心舱”的径向端口后,神舟十四号和核心舱之间形成-条直径80cm、长约1m的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道"的体积是立方米。21. 小温观看了神舟十四号载人飞船发射后,打算做一个火箭模型,他把棱长8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱体和一个圆锥体(如图),其中这个圆锥体的体积是立方厘米。
20. 神舟十四号载人飞船采用自主快速交会对接模式,当它成功对接于“天和核心舱”的径向端口后,神舟十四号和核心舱之间形成-条直径80cm、长约1m的圆形通道,这是航天员进入空间站的“生命通道”。这个“生命通道"的体积是立方米。21. 小温观看了神舟十四号载人飞船发射后,打算做一个火箭模型,他把棱长8cm的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱体和一个圆锥体(如图),其中这个圆锥体的体积是立方厘米。 22. “全城志愿”正成为鹿城文明新风尚,某志愿小队有25名队员,那么他们中至少有 人是同一个月出生的。在他们中选择5人担任小组长,那么至少有人的性别是相同的。
22. “全城志愿”正成为鹿城文明新风尚,某志愿小队有25名队员,那么他们中至少有 人是同一个月出生的。在他们中选择5人担任小组长,那么至少有人的性别是相同的。三、计算。(28分)
-
23. 直接写出得数。
214+66= 0.86-0.6= 200÷8= 12×70= 0.32=
1.5×60%= 63×= = ÷0.75= ×2.6-2.6×0=
24. 递等式计算,怎样简便就怎样算。①42×()
②7.5×(26-10)+9.7
③0.8×4×12.5×2.5
④÷[1-(+0.25) ]
25. 解方程或解比例。(1)、 x-2.6=5.4(2)、x:=12:四、图形与操作。(11分)
-
26. 在方格纸上分别画出从不同方向看到左边立体图形的形状图。
 27. 下图中每个小方格边长为1cm。
27. 下图中每个小方格边长为1cm。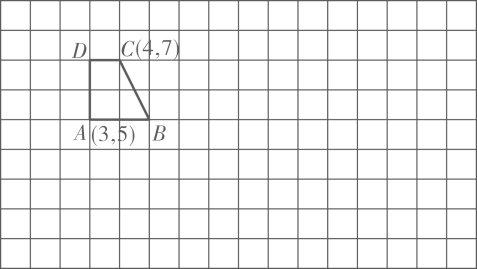 (1)、已知点A、点C的位置用数对表示分别为(3,5)和(4,7),那么点B和点D用数对表示分别为和。(2)、画出梯形按3:1放大后的图形。(3)、放大后的梯形的面积是cm2 .28. 如图,长方形OABC长3cm,宽2cm,求阴影部分的面积。
(1)、已知点A、点C的位置用数对表示分别为(3,5)和(4,7),那么点B和点D用数对表示分别为和。(2)、画出梯形按3:1放大后的图形。(3)、放大后的梯形的面积是cm2 .28. 如图,长方形OABC长3cm,宽2cm,求阴影部分的面积。
五、解决问题。(28分)我们周边的世界是丰富多彩的,用心观察就能发现很多数学信息,提出很多数学问题。
-
29. 去年我市全年节水8340万立方米,相当于减少碳排放8.34吨。如果节水9200万立方米,相当于减少碳排放多少吨?30. 目前我市人均体育场地面积是2.3平方米,根据《温州市全民健身实施计划(202-2025年)》,到2025年我市人均体育场地面积要达到2.8平方米以上。假设2025年人均体育场地面积是2.8平方米,那么比目前人均体育场地面积提高了百分之几?(百分号前保留整数)31. 鹿城区为助力企业复工复产,推出了“共享订单”模式,让缺工企业与劳动力富余企业之间实现“共享用工”,有效解决了“用工荒”和“用工闲”的矛盾。(1)、该鞋厂去年订单量是多少万双?
某鞋厂订单量比去年增长30%,达到1560万双鞋的生产任务。
(2)、甲、乙两个鞋厂接到了一个9600双的“共享订单”,甲鞋厂单独完成需要12天,乙鞋厂单独完成需要8天,那么甲、乙两厂合作完成该订单需要多少天?32. 一个密封的长方体容器装了一些水。当横着放入一个圆柱体铁块时,恰好完全浸没在水中,水深2cm(如图1)。如果把这个容器如图2放置,圆柱体铁块的刚好露出水面,且水深5.5cm。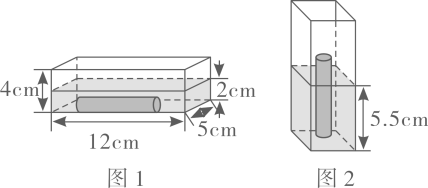 (1)、当把这个容器如图2放时,占地面积是多少?(2)、这个圆柱体铁块的体积是多少立方厘米?33. “双减”后为丰富学生的课余生活,某校开展学生课后社团活动,小年调在了六(1)班同学各社团参与人数,绘制了下面两幅统计图(不完整)。
(1)、当把这个容器如图2放时,占地面积是多少?(2)、这个圆柱体铁块的体积是多少立方厘米?33. “双减”后为丰富学生的课余生活,某校开展学生课后社团活动,小年调在了六(1)班同学各社团参与人数,绘制了下面两幅统计图(不完整)。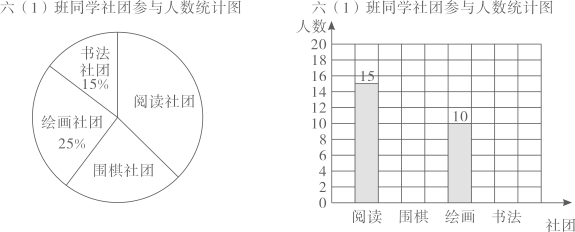 (1)、参与本次调查一共有多少人?(2)、请把条形统计图补充完整。(3)、已知该校六年级共有280名学生,根据小年的统计结果,请你推算该校六年级学生参加阅读社团的大概有多少人?
(1)、参与本次调查一共有多少人?(2)、请把条形统计图补充完整。(3)、已知该校六年级共有280名学生,根据小年的统计结果,请你推算该校六年级学生参加阅读社团的大概有多少人?六、阅读与思考(附加题:10分)
-
34. 数学学习要重视推理能力的培养,我们应逐步养成重论据、合乎逻辑的思维习惯,形成实事求是的科学态度和理性精神。
例如,数学书上有这样一个例子:如图,你能推出∠1=∠3吗?我们可以这样进行推理和证明:
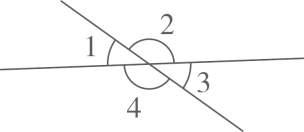
因为∠1+∠2=平角=180°,∠2+∠3=平角=180°,
所以∠1=180°-∠2,∠3=180°-∠2,
又因为180°-∠2=180°-∠2,
所以∠1=∠3.
(1)、如图,把三角形ABC的边AC延长到点D,你能推导出∠2+∠3=∠4吗?请把下面的推导过程填完整:
因为三角形的内角和是180°,
所以∠1+∠2+∠3=。
所以∠2+∠3=180°-∠ ,
又因为∠1+∠4=平角=180°,
所以∠4=180°-∠ ,
所以∠2+∠3=∠4。
(2)、一个五边形的内角和是540°(如图),试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。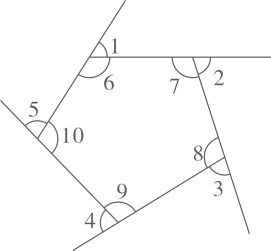
请写出你的推导过程: