广东省广州市增城区2022-2023学年八年级下学期数学期中试卷
试卷更新日期:2023-05-26 类型:期中考试
一、单选题
-
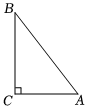
1. 若在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 如图,在中, , , , 则的长为( )
 A、 B、 C、 D、3. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、4. 下列各组数中,能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , , 点A在点O的北偏西方向,则点B在点O的( )
A、 B、 C、 D、3. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、4. 下列各组数中,能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 下列计算正确的是( )A、 B、 C、 D、6. 如图, , , , 点A在点O的北偏西方向,则点B在点O的( )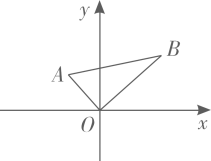 A、北偏东 B、北偏东 C、东偏北 D、东偏北7. 如图,在正方形的外侧作等边三角形 , 则度数为( )
A、北偏东 B、北偏东 C、东偏北 D、东偏北7. 如图,在正方形的外侧作等边三角形 , 则度数为( ) A、 B、 C、 D、8. 矩形具有而菱形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分9. 下列命题中,逆命题是真命题的是( )A、两直线平行,内错角相等 B、若a=b,那么a2=b2 C、对顶角相等 D、若a=b,那么|a|=|b|10. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A、 B、 C、 D、8. 矩形具有而菱形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分9. 下列命题中,逆命题是真命题的是( )A、两直线平行,内错角相等 B、若a=b,那么a2=b2 C、对顶角相等 D、若a=b,那么|a|=|b|10. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )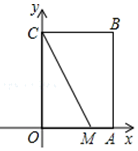 A、(3,1)或(3,3) B、(3,)或(3,3) C、(3,)或(3,1) D、(3,)或(3,1)或(3,3)
A、(3,1)或(3,3) B、(3,)或(3,3) C、(3,)或(3,1) D、(3,)或(3,1)或(3,3)二、填空题
-
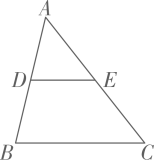
11. 如图,在中,点D、E分别是边、的中点, , 则 .
 12. 如图,在平行四边形中, , 周长是 , 则AB= .
12. 如图,在平行四边形中, , 周长是 , 则AB= .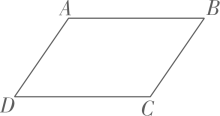 13. 计算: × =.14. 如图,八年级的小明和小亮同学学习了“勾股定理”之后,为了测得如图所示风筝的高度 , 他们进行了如下操作:
13. 计算: × =.14. 如图,八年级的小明和小亮同学学习了“勾股定理”之后,为了测得如图所示风筝的高度 , 他们进行了如下操作:测得米;(注:)
根据手中剩余线的长度计算出风筝线米;
牵线放风筝的小明身高米.
则风筝的高度CE是米
 15. 如图,数轴上点A表示的数为a,化简: .
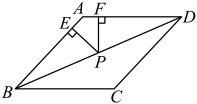
15. 如图,数轴上点A表示的数为a,化简: .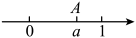 16. 如图,菱形的周长为20,面积为24,P是对角线上一点,分别作P点到直线、的垂线段、 , 则等于
16. 如图,菱形的周长为20,面积为24,P是对角线上一点,分别作P点到直线、的垂线段、 , 则等于
三、解答题
-
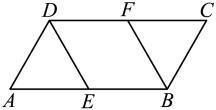
17. 已知 = ,求代数式 的值.18. 计算: .19. 已知,如图,中,E,F分别是边、的中点.求证:四边形 是平行四边形.
 20. 如图,点D在中, , , , .
20. 如图,点D在中, , , , .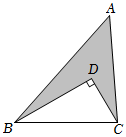 (1)、求的长;(2)、求图中阴影部分的面积.21. 如图,将长方形纸片 沿对角线 折叠,点 落在点 处, 与 相交于点 .
(1)、求的长;(2)、求图中阴影部分的面积.21. 如图,将长方形纸片 沿对角线 折叠,点 落在点 处, 与 相交于点 .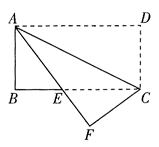 (1)、求证: ;(2)、若 , ,求 的长.22. 如图,在笔直的公路旁有一座山,从山另一边的C处到公路上的停靠站A的距离为 , 与公路上另一停靠站B的距离为 , 停靠站A、B之间的距离为 , 为方便运输货物现要从公路上的D处开凿隧道修通一条公路到C处,且 .
(1)、求证: ;(2)、若 , ,求 的长.22. 如图,在笔直的公路旁有一座山,从山另一边的C处到公路上的停靠站A的距离为 , 与公路上另一停靠站B的距离为 , 停靠站A、B之间的距离为 , 为方便运输货物现要从公路上的D处开凿隧道修通一条公路到C处,且 .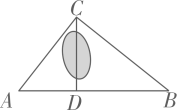 (1)、请判断的形状?(2)、求修建的公路的长.23. 如图,在中,平分 , 交于点D.
(1)、请判断的形状?(2)、求修建的公路的长.23. 如图,在中,平分 , 交于点D.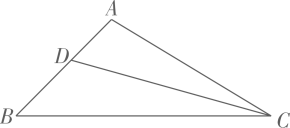 (1)、尺规作图:作的垂直平分线,分别交 , 于点E,F,连接 , ;(不写作法,保留作图痕迹)24. 材料一:两个含有二次根式而非零的代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式.
(1)、尺规作图:作的垂直平分线,分别交 , 于点E,F,连接 , ;(不写作法,保留作图痕迹)24. 材料一:两个含有二次根式而非零的代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式.例如: , 我们称的一个有理化因式是 .
材料二:如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.
例如: .
请你仿照材料中的方法探索并解决下列问题:
(1)、 的有理化因式为 ;(2)、将式子分母有理化;(3)、化简: .25. 如图 , 在正方形中,M是边上的一点,连接 , 作于点M,交正方形的外角的平分线于点N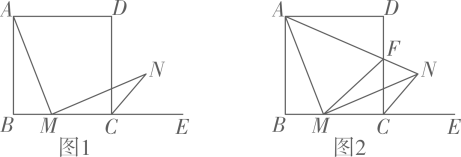 (1)、若正方形的边长为 , 当M是边上的中点时,求的长;(2)、求证:;(3)、如图2,连接 , 交边于点F,连接 , 探究线段、和之间的数量关系,并说明理由.
(1)、若正方形的边长为 , 当M是边上的中点时,求的长;(2)、求证:;(3)、如图2,连接 , 交边于点F,连接 , 探究线段、和之间的数量关系,并说明理由.