广东省广州市花都区2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中，属最简二次根式的是（）

A、 $\sqrt{\frac{1}{4}}$ B、 $\sqrt{1.5}$ C、 $\sqrt{8}$ D、 $\sqrt{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{6} = \sqrt{9}$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{7}$ C、 $\sqrt{5} + 3 \sqrt{5} = 4 \sqrt{5}$ D、 $\sqrt{6} - \sqrt{3} = \sqrt{3}$

查看试题解析
3. 要使二次根式 $\sqrt{2 - x}$ 有意义，x应满足的条件是（）

A、 $x \geq 2$ B、 $x \leq 2$ C、 $x > 2$ D、 $x < 2$

查看试题解析
4. 下列各组数据中的三个数，分别作为三角形的三边长，能构成直角三角形的是（）

A、1，2，3 B、2， $\sqrt{2}$ ， $\sqrt{3}$ C、8，24，25 D、9，12，15

查看试题解析
5. 如图，在菱形 $A B C D$ 中， $∠ B A D = 120 °$ ， $A C = 5$ ，则菱形 $A B C D$ 的周长是（）

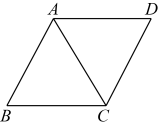A、10 B、15 C、20 D、30

查看试题解析
6. 下列说法错误的是（）

A、菱形的对角线互相垂直且平分 B、矩形的对角线相等 C、有一组邻边相等的四边形是菱形 D、四条边相等的四边形是菱形

查看试题解析
7. 如图， $▱ A B C D$ 的对角线 $A C ， B D$ 相交于点O，点 $E ， F$ 分别是线段 $A O ， B O$ 的中点，若 $A C + B D = 24$ 厘米， $△ O A B$ 的周长是18厘米，则 $E F$ 的长度是（）．

A、 $3 cm$ B、 $6cm$ C、 $10cm$ D、 $12cm$

查看试题解析
8. 如图，已知实数a在数轴上的对应点位置如图所示，则化简 $\sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、a-2 B、-a-2 C、1 D、2-a

查看试题解析
9. 等边三角形的边长为2，则该三角形的面积为（　　）

A、4 $\sqrt{3}$ B、 $\sqrt{3}$ C、2 $\sqrt{3}$ D、3

查看试题解析
10. 观察下组数据，寻找规律：0、 $- \sqrt{2}$ 、2、 $- \sqrt{6}$ 、 $2 \sqrt{2}$ 、 $- \sqrt{10}$ ……那么第10个数据是（）

A、 $2 \sqrt{6}$ B、 $- 3 \sqrt{2}$ C、7 D、 $- \sqrt{30}$

查看试题解析

二、填空题

11. $\sqrt{3} + \sqrt{27} =$ ．

查看试题解析
12. 已知 $\sqrt{20 n}$ 是整数，则满足条件的最小正整数n为

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D是AB的中点，且 $D C = 5 cm$ ，则AB＝cm．

查看试题解析
14. 如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是．

查看试题解析
15. 如图E在边AB上，把矩形ABCD沿直线DE折叠，点A落在边BC上的点F处．若AE＝5，BF＝3．则△CDF的面积是．

查看试题解析

三、解答题

16. 计算： $\sqrt{6} \div \sqrt{2} + | 1 - \sqrt{3} | - \sqrt{12} + {(\frac{1}{2})}^{- 1}$ ；

查看试题解析
17. 已知：如图，点E ， F是平行四边形 $A B C D$ 中 $A B ， D C$ 边上的点，且 $A E = C F$ ，连接 $D E ， B F$ ．求证： $D E = B F$ ．

查看试题解析
18. 已知 $x = 2 - \sqrt{2}$ ， $y = 2 + \sqrt{2}$ ，求下列各式的值：

(1)、 $x^{2} + 2 x y + y^{2}$

(2)、 $\frac{y}{x} - \frac{x}{y}$

查看试题解析
19. 我市某中学有一块四边形的空地 $A B C D$ ，如图所示，为了绿化环境，学校计划在空地上种植草皮，经测量 $∠ B = 90 °$ ， $A B = 6 m$ ， $B C = 8 m$ ， $C D = 24 m$ ， $A D = 26 m$ ．

(1)、求出空地 $A B C D$ 的面积；

(2)、若每种植1平方米草皮需要350元，问总共需投入多少元？

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A D > A B$ ．

(1)、尺规作图：作 $D C$ 边的垂直平分线，分别交 $A D$ 、 $C D$ 边于点E、F（要求：保留作图痕迹，不写作法）；

(2)、连接 $E C$ ，若 $∠ B A D = 130 °$ ，求 $∠ A E C$ 的度数．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ，过点D作 $∠ A D C$ 的角平分线交 $A B$ 于点E，连接 $A C$ 交 $D E$ 于点O， $A D ∥ C E$ ．

(1)、求证：四边形 $A E C D$ 是菱形；

(2)、若 $A D = 10$ ， $△ A C D$ 的周长为36，求菱形 $A E C D$ 的面积．

查看试题解析
22. 小明在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值，他是这样分析与解答的：
因为 $a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，所以 $a - 2 = - \sqrt{3}$ ．

所以 ${(a - 2)}^{2} = 3$ ，即 $a^{2} - 4 a + 4 = 3$ ．所以 $a^{2} - 4 a = - 1$ ．

所以 $2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．

请根据小明的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1} =$ ；

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \cdot \cdot \cdot + \frac{1}{\sqrt{100} + \sqrt{99}}$ ；

(3)、若 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $4 a^{2} - 8 a + 1$ 的值．

查看试题解析
23. 如图，在平面直角坐标系中， $A B // O C$ ， $A (0 ， 12)$ ， $B (a ， c)$ ， $C (b ， 0)$ ，并且a ， b满足 $b = \sqrt{a - 20} +$ $\sqrt{20 - a} + 16$ ．动点P从点A出发，在线段 $A B$ 上以每秒2个单位长度的速度向点B运动；动点Q从点O出发，在线段 $O C$ 上以每秒1个单位长度的速度向点C运动，点P ， Q分别从点A ， O同时出发，当点P运动到点B时，点Q随之停止运动．设运动时间为t秒．

(1)、直接写出B ， C两点的坐标；

(2)、当t为何值时，四边形 $P Q C B$ 是平行四边形？

(3)、当t为何值时， $△ P Q C$ 是以 $P Q$ 为腰的等腰三角形？并求出P ， Q两点的坐标．

查看试题解析