北京市通州区2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-05-26 类型:期中考试
一、单选题
-
1. 函数的自变量x的取值范围是( )A、 B、 C、 D、全体实数2. 如图1所示的是被称作“通州八景”之一的燃灯佛舍利塔,它巍峨挺拔,雄伟壮观,始建于北周年间,是北京地区建造年代最早、最高大的佛塔之一.燃灯佛舍利塔为八角形十三层砖木结构密檐式塔,十三层均为正八边形砖木结构,图2所示的正八边形是其中一层的平面示意图,其内角和为( )
 A、 B、 C、 D、3. 如图所示是围棋棋盘的一部分,将它放置在平面直角坐标系中,若白棋②的坐标是 , 白棋③的坐标是 , 则黑棋①的坐标是( )
A、 B、 C、 D、3. 如图所示是围棋棋盘的一部分,将它放置在平面直角坐标系中,若白棋②的坐标是 , 白棋③的坐标是 , 则黑棋①的坐标是( )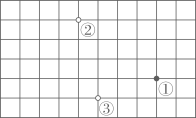 A、 B、 C、 D、4. 如图,在中, , , 则的度数是( )
A、 B、 C、 D、4. 如图,在中, , , 则的度数是( ) A、40° B、50° C、60° D、70°5. 如图,矩形的对角线相交于点O , , , 则矩形对角线的长为( )
A、40° B、50° C、60° D、70°5. 如图,矩形的对角线相交于点O , , , 则矩形对角线的长为( )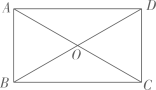 A、4 B、8 C、 D、6. 下列命题正确的是( ).A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、有一组邻边相等且有一个角是直角的平行四边形是正方形7. 如图,在平面直角坐标系中,菱形 , O为坐标原点,点C在x轴上,A的坐标为 , 则顶点B的坐标是( )
A、4 B、8 C、 D、6. 下列命题正确的是( ).A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、有一组邻边相等且有一个角是直角的平行四边形是正方形7. 如图,在平面直角坐标系中,菱形 , O为坐标原点,点C在x轴上,A的坐标为 , 则顶点B的坐标是( )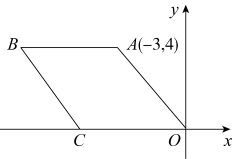 A、 B、 C、 D、8. 如图,若点 为函数 图象上的一动点, 表示点 到原点 的距离,则下列图象中,能表示 与点 的横坐标 的函数关系的图象大致是( ).
A、 B、 C、 D、8. 如图,若点 为函数 图象上的一动点, 表示点 到原点 的距离,则下列图象中,能表示 与点 的横坐标 的函数关系的图象大致是( ). A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 在平面直角坐标系中,点关于x轴的对称点的坐标是 .10. 如图,在中,点E在上,平分 , 若 , , 则 .
 11. 函数y=kx(k0)的图象上有两个点A1( , ),A2( , ),当<时,> , 写出一个满足条件的函数解析式.12. 如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是(写出一个即可).
11. 函数y=kx(k0)的图象上有两个点A1( , ),A2( , ),当<时,> , 写出一个满足条件的函数解析式.12. 如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是(写出一个即可). 13. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则方程组的解是.
13. 如图,直线y=x+b与直线y=kx+6交于点P(3,5),则方程组的解是. 14. 图1中菱形的两条对角线长分别为6和8,将其沿对角线裁分为四个三角形,将这四个三角形无重叠地拼成如图2所示的图形,则图1中菱形的面积等于;图2中间的小四边形的面积等于 .
14. 图1中菱形的两条对角线长分别为6和8,将其沿对角线裁分为四个三角形,将这四个三角形无重叠地拼成如图2所示的图形,则图1中菱形的面积等于;图2中间的小四边形的面积等于 .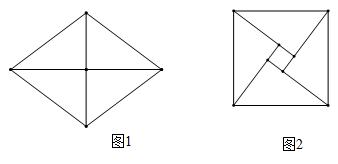 15. 如图,矩形纸片 , , , 折叠纸片使边与对角线重合,折痕为 , 则 , .
15. 如图,矩形纸片 , , , 折叠纸片使边与对角线重合,折痕为 , 则 , . 16. 如图,点A , B , C在一次函数的图象上,它们的横坐标依次为-1,0.5,2.分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是 .
16. 如图,点A , B , C在一次函数的图象上,它们的横坐标依次为-1,0.5,2.分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是 .
三、解答题
-
17. 如图,在中,于点E , 于点F . 求证: .
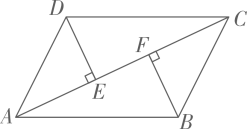 18. 在平面直角坐标系xOy中,一次函数的图象与x轴、y轴分别交于点A、B ,
18. 在平面直角坐标系xOy中,一次函数的图象与x轴、y轴分别交于点A、B ,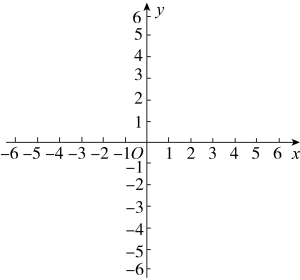 (1)、求点A , B的坐标;(2)、画出该函数的图象;(3)、点 , 连结 , 求的面积.19. 下面是小明设计的“作矩形ABCD”的尺规作图过程:
(1)、求点A , B的坐标;(2)、画出该函数的图象;(3)、点 , 连结 , 求的面积.19. 下面是小明设计的“作矩形ABCD”的尺规作图过程:已知:在中,∠ABC=90°.
求作:矩形ABCD .
作法:如图,
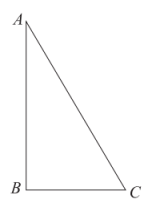
①分别以点A , C为圆心、大于的长为半径作弧,两弧相交于E , F两点;
②作直线EF , 交AC于点P;
③连接BP并延长至点D , 使得PD=BP;
④连接AD , CD .
则四边形ABCD是矩形.
根据小明设计的尺规作图过程,解决以下问题:
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接AE , CE , AF , CF .
∵AE=CE , AF=CF ,
∴EF是线段AC的垂直平分线.
∴AP= .
又∵BP=DP ,
∴四边形ABCD是平行四边形(填推理的依据).
∵∠ABC=90°,
∴四边形ABCD是矩形(填推理的依据).
20. 在平面直角坐标系中,直线与直线交于点 . (1)、求点A的坐标及直线的表达式;(2)、若P是坐标轴上一点(不与点O重合),且满足 , 求点P的坐标.21. 定义:若点P为四边形内一点,且满足 , 则称点P为四边形的一个“互补点”.(1)、如图1,点P为四边形的一个“互补点”,若 , 则;
(1)、求点A的坐标及直线的表达式;(2)、若P是坐标轴上一点(不与点O重合),且满足 , 求点P的坐标.21. 定义:若点P为四边形内一点,且满足 , 则称点P为四边形的一个“互补点”.(1)、如图1,点P为四边形的一个“互补点”,若 , 则;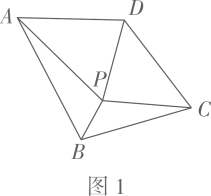 (2)、如图2,点P是菱形对角线上的任意一点(不与点B , D重合),求证:点P为菱形的一个“互补点”.
(2)、如图2,点P是菱形对角线上的任意一点(不与点B , D重合),求证:点P为菱形的一个“互补点”.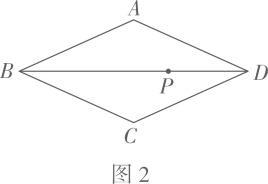 22. 为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反应的是每月水费y(元)与用水量x(吨)之间的函数关系.
22. 为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反应的是每月水费y(元)与用水量x(吨)之间的函数关系. (1)、小乐家五月份用水8吨,应交水费多少元?(2)、按上述分段收费标准,小乐家三月份交水费36元,问三月份用水多少吨?23. 在平面直角坐标系中,一次函数的图象经过点 , 点 .
(1)、小乐家五月份用水8吨,应交水费多少元?(2)、按上述分段收费标准,小乐家三月份交水费36元,问三月份用水多少吨?23. 在平面直角坐标系中,一次函数的图象经过点 , 点 . (1)、求k , b的值;(2)、当时,对于x的每一个值,函数的值小于一次函数的值,直接写出n的取值范围.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接AE、CE.
(1)、求k , b的值;(2)、当时,对于x的每一个值,函数的值小于一次函数的值,直接写出n的取值范围.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接AE、CE.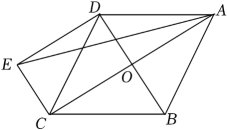 (1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为2,∠BCD=60°,求AE的长.25. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.(1)、绘制函数图象
(1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为2,∠BCD=60°,求AE的长.25. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.(1)、绘制函数图象①列表:下表是x与y的几组对应值,其中m=;
x
…
0
1
2
3
…
y
…
1
2
3
4
3
m
1
…
②描点:根据表中的数值描点 , 补充描出点;
③连线:用平滑的曲线顺次连接各点,画出函数图象.
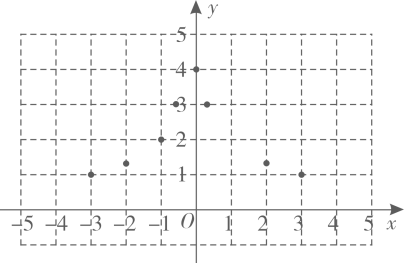 (2)、探究函数性质
(2)、探究函数性质写出函数的一条性质: .
(3)、运用函数图象及性质①观察你所画的函数图象,回答问题:若点 , 为该函数图象上不同的两点,则;
②根据函数图象,写出不等式的解集是 .