人教版八年级下数学期末复习知识点扫盲满分计划——17.2勾股定理逆定理
试卷更新日期:2023-05-26 类型:复习试卷
一、判断三边是否构成直角三角形
-
1. 如图,为了测量池塘的宽度DE,在池塘周围的平地上选择了A、B、C三点,且A、D、E、C四点在同一条直线上,∠C=90°,已测得AB=100m,BC=60m,AD=20m,EC=10m,求池塘的宽度DE.
 2. 下列各组数中不能作为直角三角形的三边长的是( )A、9,12,15 B、6, 8, 10 C、 , 2,3 D、1.5,2.5, 3.53. 已知的三边长为、、 , 且 , , , 试判断的形状,并说明理由.4. 如图,在中,长比长大1, , D是上一点, , .
2. 下列各组数中不能作为直角三角形的三边长的是( )A、9,12,15 B、6, 8, 10 C、 , 2,3 D、1.5,2.5, 3.53. 已知的三边长为、、 , 且 , , , 试判断的形状,并说明理由.4. 如图,在中,长比长大1, , D是上一点, , .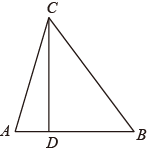 (1)、求证:;(2)、求长.5. 如图,四边形ABCD中,若∠B=90°,AB=20,BC=15,CD=7,AD=24.
(1)、求证:;(2)、求长.5. 如图,四边形ABCD中,若∠B=90°,AB=20,BC=15,CD=7,AD=24.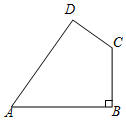 (1)、判断∠D是否是直角,并说明理由;(2)、求∠A+∠C的度数.6. 在中,已知 , , , 试判断的形状,并说明理由.
(1)、判断∠D是否是直角,并说明理由;(2)、求∠A+∠C的度数.6. 在中,已知 , , , 试判断的形状,并说明理由.二、网格中判断直角三角形
-
7. 如图,每个小正方形的边长为1
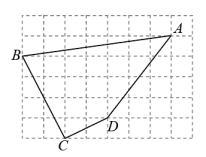 (1)、求四边形的周长;(2)、是直角吗?说明理由.8. 正方形网格中的每个小正方形的边长都是一个单位,每个小正方形的顶点叫做格点.已知均为格点,仅用无刻的直尺作出符合下列问题的图形.
(1)、求四边形的周长;(2)、是直角吗?说明理由.8. 正方形网格中的每个小正方形的边长都是一个单位,每个小正方形的顶点叫做格点.已知均为格点,仅用无刻的直尺作出符合下列问题的图形. (1)、在图1中,线段 , 度;(2)、在图1中,在上作出点使得;(3)、在图2中,交其中一条网格线于点E,在平面中作一个点F,使得 ,(4)、在图3中,点A是格点,点P在网格线上,将线段向左平移三个单位得线段.9. 如图,正方形网格中的每个小正方形边长都是 , 每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(不需要写画法).
(1)、在图1中,线段 , 度;(2)、在图1中,在上作出点使得;(3)、在图2中,交其中一条网格线于点E,在平面中作一个点F,使得 ,(4)、在图3中,点A是格点,点P在网格线上,将线段向左平移三个单位得线段.9. 如图,正方形网格中的每个小正方形边长都是 , 每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(不需要写画法). (1)、在图中,画一个正方形,使它的面积是;(2)、在图中,画一个三角形 , 使它的三边长分别为:、、 , 并计算边上的高为 . (直接写出结果)10. 如图,每个小正方形的边长都为1,的顶点均在格点上.
(1)、在图中,画一个正方形,使它的面积是;(2)、在图中,画一个三角形 , 使它的三边长分别为:、、 , 并计算边上的高为 . (直接写出结果)10. 如图,每个小正方形的边长都为1,的顶点均在格点上.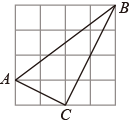 (1)、判断的形状,并说明理由;(2)、求AB边上的高h.11. 如图,每个小正方形的边长都为1.
(1)、判断的形状,并说明理由;(2)、求AB边上的高h.11. 如图,每个小正方形的边长都为1. (1)、求的周长.(2)、求的大小.
(1)、求的周长.(2)、求的大小.三、利用勾股定理逆定理求解
-
12. 如图已知中, , , 边上的中线 , 则的面积为( ) .
 A、30 B、130 C、60 D、12013. 如图,小区有一块三角形空地 , 为响应中山市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路隔开, . 经测量,米,米,米,米.
A、30 B、130 C、60 D、12013. 如图,小区有一块三角形空地 , 为响应中山市创建全国文明典范城市的号召,小区计划将这块空地种上三种不同的花卉,中间用小路隔开, . 经测量,米,米,米,米. (1)、求的长;(2)、求小路的长14. 已知等腰的底边 , D是腰上一点,且 , , 则的长为.
(1)、求的长;(2)、求小路的长14. 已知等腰的底边 , D是腰上一点,且 , , 则的长为. 15. 如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
15. 如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°. (1)、判断∠D是否是直角,并说明理由.(2)、求四边形ABCD的面积.16. 如图,在△ABC中,∠B=90°,AB=1,BC=2.四边形ADEC是正方形,则正方形ADEC的面积是( )
(1)、判断∠D是否是直角,并说明理由.(2)、求四边形ABCD的面积.16. 如图,在△ABC中,∠B=90°,AB=1,BC=2.四边形ADEC是正方形,则正方形ADEC的面积是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6四、勾股定理逆定理的实际应用
-
17. 如图,甲乙两船从港口A同时出发,甲船以16海里/时的速度向北偏东40°方向航行,乙船向南偏东50°方向航行,小时后,甲船到达C岛,乙船到达B岛,若CB两岛相距17海里,问乙船的航速是多少?
 18. 八(2)班数学兴趣小组来到操场上测量旗杆的高度,小强测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图①),小云拉着绳子的下端往后退,当她将绳子拉直时,小晨测得此时小云拉绳子的手到地面的距离为1米,到旗杆的距离为8米(如图②),请你求出旗杆的高度.
18. 八(2)班数学兴趣小组来到操场上测量旗杆的高度,小强测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米(如图①),小云拉着绳子的下端往后退,当她将绳子拉直时,小晨测得此时小云拉绳子的手到地面的距离为1米,到旗杆的距离为8米(如图②),请你求出旗杆的高度. 19. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
19. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?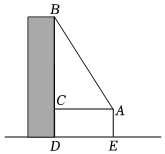 20. 今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
20. 今年第6号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.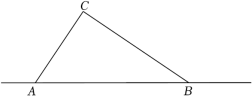 (1)、求∠ACB的度数;(2)、海港C受台风影响吗?为什么?(3)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?21. 如图,一条笔直的竹竿斜靠在一道垂直于地面的墙面上,一端在墙面A处,另一端在地面B处,墙角记为点C.
(1)、求∠ACB的度数;(2)、海港C受台风影响吗?为什么?(3)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?21. 如图,一条笔直的竹竿斜靠在一道垂直于地面的墙面上,一端在墙面A处,另一端在地面B处,墙角记为点C. (1)、若 米, 米.
(1)、若 米, 米.①竹竿的顶端A沿墙下滑1米,那么点B将向外移动多少米?
②竹竿的顶端从A处沿墙 下滑的距离与点B向外移动的距离,有可能相等吗?如果不可能,请说明理由;如果可能,请求出移动的距离(保留根号).
(2)、若 ,则顶端A下滑的距离与底端B外移的距离,有可能相等吗?若能相等,请说明理由;若不等,请比较顶端A下滑的距离与底端B外移的距离的大小.五、平面展开最短路径
-
22. 如图,正方体的棱长为3 cm,已知点B与点C间的距离为1 cm,一只蚂蚁沿着正方体的表面从点A爬到点C,需要爬行的最短距离为 .
 23. 如图是长、宽、高的长方体容器.
23. 如图是长、宽、高的长方体容器. (1)、求底面矩形的对角线的长;(2)、长方体容器内可完全放入的棍子最长是多少?24. 如图1,在正方形中,E是的中点.
(1)、求底面矩形的对角线的长;(2)、长方体容器内可完全放入的棍子最长是多少?24. 如图1,在正方形中,E是的中点. (1)、若 , 求的长.(2)、如图2,F是线段上的一点,且 , 求证:是直角三角形.(3)、如图3是一个正方体,棱长 , 的中点E处有一只蚂蚁,蚂蚁从处出发在正方体表面爬行,经过上某点P处后继续沿直线方向爬到正方体的顶点G处.当的值最小时,求的长.25. 如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
(1)、若 , 求的长.(2)、如图2,F是线段上的一点,且 , 求证:是直角三角形.(3)、如图3是一个正方体,棱长 , 的中点E处有一只蚂蚁,蚂蚁从处出发在正方体表面爬行,经过上某点P处后继续沿直线方向爬到正方体的顶点G处.当的值最小时,求的长.25. 如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( ) A、 B、 C、120 D、13026. 如图,长方体的长 , 宽 , 高 , 点M在上,且 , 一只蚂蚁如果要沿着长方体的表面从点A爬到点N,需要爬行的最短距离是.
A、 B、 C、120 D、13026. 如图,长方体的长 , 宽 , 高 , 点M在上,且 , 一只蚂蚁如果要沿着长方体的表面从点A爬到点N,需要爬行的最短距离是.
六、综合训练
-
27. 如图,已知 , ,
 (1)、求AB的长;(2)、求的面积.28. 在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点.
(1)、求AB的长;(2)、求的面积.28. 在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点.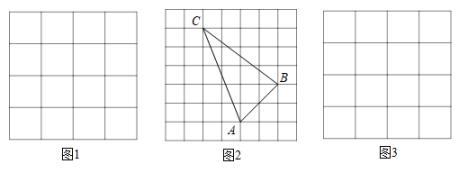 (1)、在图1中,以格点为顶点画 , 使三边长分别为、、;(2)、如图2,各顶点均在格点上,求的面积和点到的距离;(3)、在图3中,以格点为顶点画直角边长为无理数的等腰直角三角形,并说明理由.29. 在边长为1的小正方形组成的网格中,A,B,C,D、E在格点上,长度是的线段是( )
(1)、在图1中,以格点为顶点画 , 使三边长分别为、、;(2)、如图2,各顶点均在格点上,求的面积和点到的距离;(3)、在图3中,以格点为顶点画直角边长为无理数的等腰直角三角形,并说明理由.29. 在边长为1的小正方形组成的网格中,A,B,C,D、E在格点上,长度是的线段是( ) A、AB B、AC C、AD D、AE30. 如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )
A、AB B、AC C、AD D、AE30. 如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )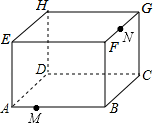 A、20cm B、2cm C、(12+2)cm D、18cm
A、20cm B、2cm C、(12+2)cm D、18cm