北京市大兴区2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-05-26 类型:期中考试
一、单选题
-
1. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、2. 下列运算中,结果正确的是( )A、 B、 C、 D、3. 如图,在四边形ABCD中,ABCD.下列条件不能判定此四边形为平行四边形的是( )
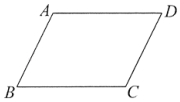 A、AB=CD B、ADBC C、∠B=∠D D、AD=BC4. 下列不是轴对称图形的是( )A、有一个角是的直角三角形 B、矩形 C、菱形 D、正方形5. 如图,有一根电线杆在离地面处的A点断裂,此时电线杆顶部C点落在离电线杆底部B点远的地方,则此电线杆原来长度为( )
A、AB=CD B、ADBC C、∠B=∠D D、AD=BC4. 下列不是轴对称图形的是( )A、有一个角是的直角三角形 B、矩形 C、菱形 D、正方形5. 如图,有一根电线杆在离地面处的A点断裂,此时电线杆顶部C点落在离电线杆底部B点远的地方,则此电线杆原来长度为( )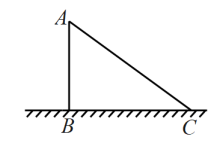 A、 B、 C、 D、6. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A、 B、 C、 D、6. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )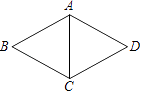 A、20 B、15 C、10 D、57. 如图,在中, , , 的垂直平分线交于点E,交于点F,连接 , 则的周长是( )
A、20 B、15 C、10 D、57. 如图,在中, , , 的垂直平分线交于点E,交于点F,连接 , 则的周长是( )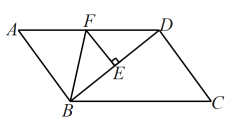 A、6 B、8 C、9 D、108. 如图,在中, , 射线平分 , 于点D , 于点E , 若F为的中点,连接 . 下列结论:①;②;③;④ . 其中正确结论的序号是( )
A、6 B、8 C、9 D、108. 如图,在中, , 射线平分 , 于点D , 于点E , 若F为的中点,连接 . 下列结论:①;②;③;④ . 其中正确结论的序号是( )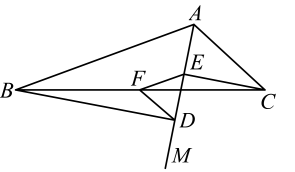 A、①②④ B、①③④ C、②③ D、①②③④
A、①②④ B、①③④ C、②③ D、①②③④二、填空题
-
9. 若在实数范围内有意义,则x的取值范围是 .
10. 比较大小:(填“>”,“<”或“=”).11. 化简:.12. 如图,为了测量池塘边上A , B两点间的距离,在池塘外选一点C , 分别连接和并延长到点D , E , 使 , , 连接 . 若测得 , 则A , B两点间距离是m. 13. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 .
13. 如图,在菱形ABCD中,若AC=6,BD=8,则菱形ABCD的面积是 . 14. 如图,矩形的对角线相交于点O , 若 , , 则的长是 .
14. 如图,矩形的对角线相交于点O , 若 , , 则的长是 . 15. 如图,在正方形中,E,F分别是边 , 上的点, . 若 , , 则的长是 .
15. 如图,在正方形中,E,F分别是边 , 上的点, . 若 , , 则的长是 .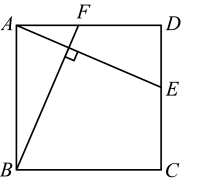 16. 如图,四边形与四边形为正方形 , 相交于点H , 连接 . 下列结论中:①;②;③平分 . 所有正确结论的序号是 .
16. 如图,四边形与四边形为正方形 , 相交于点H , 连接 . 下列结论中:①;②;③平分 . 所有正确结论的序号是 .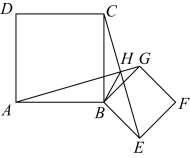
三、解答题
-
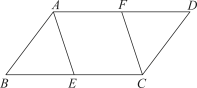
17. 计算: .18. 计算: .19. 在中, , 若 , . 求a , b的长.20. 如图,在▱ABCD中,点E , F分别为BC , AD中点,求证:四边形AECF是平行四边形.
 21. 如图,平行四边形的对角线、交于点O,点E、F在上,且求证: .
21. 如图,平行四边形的对角线、交于点O,点E、F在上,且求证: . 22. 如图,矩形纸片中, , 把矩形纸片沿直线折叠,点B落在点E处,交于点F , 若 . 求的面积.
22. 如图,矩形纸片中, , 把矩形纸片沿直线折叠,点B落在点E处,交于点F , 若 . 求的面积.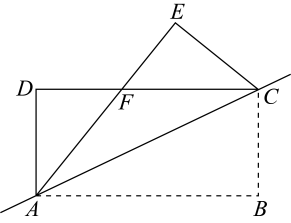 23. 如图,在中,平分 , 交于点E , 交于点F . 求证: .
23. 如图,在中,平分 , 交于点E , 交于点F . 求证: .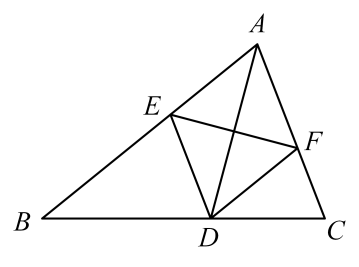 24. 如图,在四边形中, , , , . 求的度数.
24. 如图,在四边形中, , , , . 求的度数.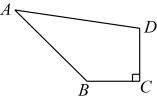 25. 如图,菱形的对角线相交于点O , 过点A作于点E , 延长到点F , 使 , 连接 .
25. 如图,菱形的对角线相交于点O , 过点A作于点E , 延长到点F , 使 , 连接 . (1)、求证:四边形AEFD是矩形;(2)、连接 , 若 , . 求的长.26. 已知 , , 有下列正确的结论:
(1)、求证:四边形AEFD是矩形;(2)、连接 , 若 , . 求的长.26. 已知 , , 有下列正确的结论:若 , 则;
若 , 则;
若 , 则 .
(1)、根据以上三个正确的结论,猜想:若 , 则;(2)、猜想与的数量关系,并证明.27. 在正方形中,E为射线上一动点(点E不与A , B重合),作 , 交直线于点F , 连接 .
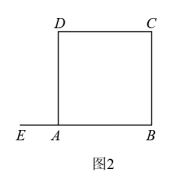 (1)、如图1,当点E在线段上时,用等式表示线段 , , 的数量关系;(2)、如图2,当点E在线段的延长线上时,
(1)、如图1,当点E在线段上时,用等式表示线段 , , 的数量关系;(2)、如图2,当点E在线段的延长线上时,①依题意补全图2;
②用等式表示线段 , , 的数量关系,并证明.
28. 在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到两条坐标轴的距离之和等于点Q到两条坐标轴的距离之和,则称P,Q两点为和谐点.例如,图1中的P,Q两点即为和谐点. (1)、已知点 .
(1)、已知点 .①在点 , , 中,点A的和谐点是;
②若点B在y轴上,且A,B两点为和谐点,则点B的坐标是;
(2)、已知点 , 点 , 连接 , 点M为线段上一点.①经过点且垂直于x轴的直线记作直线l,若在直线l上存在点N,使得M,N两点为和谐点,则n的取值范围是;
②若点 , 点 , 在以线段为斜边的等腰直角三角形的某条边上存在点K,使得M,K两点为和谐点,则m的取值范围是 .