2022~2023学年浙教版数学七年级下学期期末模考数学试卷（五）

试卷更新日期：2023-05-26 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，10小题，共30分）

1. 如列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
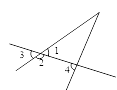
2.
如图，有下列判断①∠1与∠3是对顶角 ②∠1与∠4是内错角 ③ ∠1与∠2 是同旁内角 ④∠3与∠4是同位角，其中不正确的是（）

A、① B、② C、③ D、④

查看试题解析
3. 下列各式中，计算结果是x³+4x²-7x-28的是（）

A、（x²+7）（x+4） B、（x²-2）（x+14） C、（x+4）（x²-7） D、（x+7）（x²-4）

查看试题解析
4. 若（a^mbⁿ）³=a⁹b¹⁵ ，则m，n的值分别为（　　）

A、m=9；n=5 B、m=3；n=5 C、m=5；n=3 D、m=6；n=12

查看试题解析
5. 已知关于 $x ， y$ 的方程组 ${\begin{matrix} x + y = 2 + a \\ x - y = 3 a - 6 \end{matrix}$ ，给出下列结论：①当 $x ， y$ 互为相反数时， $a = - 2$ ；②当 $a = - 5$ 时解得 $x$ 为 $y$ 的2倍；③不论 $a$ 取什么实数， $x + 2 y$ 的值始终不变；④使 $x ， y$ 为自然数的 $a$ 的值共有4个．上述结论正确的有（）

A、①③ B、②④ C、①②③ D、①③④

查看试题解析
6. 某校八年级（1）班举行元旦晚会，晚会共有A，B，C三个节目，所有同学都参加，且每名同学只能参加一个节目，王琳同学把参加各节目的人数整理后，绘制成如图所示的扇形统计图，若参加C节目的有10人，则下列说法不正确的是（）

A、八年级（1）班共有40名学生 B、参加B节目的有9名学生 C、参加A节目所对的扇形的圆心角的度数为189° D、参加A节目的学生占全班学生的53.5%

查看试题解析
7. 已知方程组 ${\begin{array}{l} 2 x - y = 3 \\ x + 3 y = n \end{array}$ 中的x，y互为相反数，则n的值为（　　）

A、2 B、﹣2 C、0 D、4

查看试题解析
8. 若a=- $\frac{1}{5}$ ，则代数式（5a﹣4）（6a﹣7）﹣（3a﹣2）（10a﹣8）的值为（　　）

A、15 B、22 C、-15 D、9

查看试题解析
9. 一辆汽车从A地出发，向东行驶，途中要经过十字路口B，在规定的某一段时间内，若车速为每小时60千米，就能驶过B处2千米；若每小时行驶50千米，就差3千米才能到达B处，设A、B间的距离为x千米，规定的时间为y小时，则可列出方程组是（）

A、 ${\begin{array}{l} 60 y - x = 2 \\ x = 3 - 50 y \end{array}$ B、 ${\begin{array}{l} 60 y - x = 2 \\ 50 y - x = 3 \end{array}$ C、 ${\begin{array}{l} 60 y = x + 2 \\ 50 y = x - 3 \end{array}$ D、 ${\begin{array}{l} 60 y = x - 2 \\ 50 y = x - 3 \end{array}$

查看试题解析
10. 小红在超市买了一些纸杯，她把纸杯整齐地放在一起，如图，根据图中的信息，3个纸杯的高度为9cm，8个纸杯的高度为14cm.若她把70个纸杯放在一起时，纸杯的高度为（）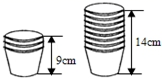

A、70 cm B、76 cm C、80 cm D、84 cm

查看试题解析

二、填空题（共6题，每题4分，共24分）

11. 已知a+b=2，a-b=-1，则a²-b²= ．

查看试题解析
12. 如图，边长为m，n（m＞n）的长方形，它的周长为12，面积为8，则（m﹣n）²的值为．

查看试题解析
13. A、B两地相距121千米，甲车和乙车的平均速度之比为4：5，两车同时从A地出发到B地，乙车比甲车早到20分钟，求甲车的平均速度．若设甲车平均速度为4x千米/小时，则所列方程是．

查看试题解析
14. 甲、乙两人练习跑步，如果乙先跑10米，则甲跑5秒就可追上乙；如果乙先跑2秒，则甲跑4秒就可追上乙，若设甲的速度为x米/秒，乙的速度为y米/秒，可列方程组.

查看试题解析
15. 在 $(x - 1) ({ax}^{3} + 3 x^{2} - bx + 1)$ 的运算结果中不含 $x^{3}$ ，且 $x^{2}$ 的系数是 $- 2$ ，那么 $a =$ ， $b =$

查看试题解析
16. 如图是根据某校为地震灾区捐款的情况而制作的统计图，已知该校在校学生有600人，请根据统计图计算该校共捐款元．

查看试题解析

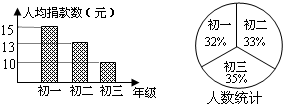
三、解答题（第17~22题每小题5分，第23、24题每小题8分）

17. 解方程组：

(1)、 ${\begin{array}{l} y = 3 x - 5 \\ - x + 2 y = 15 \end{array}$

(2)、 ${\begin{array}{l} x - 2 y = - 4 ， \\ 3 x + 4 y = 18 ． \end{array}$

查看试题解析
18. 先化简，再求值： $(1 + \frac{3}{a - 2}) \div \frac{a + 1}{a^{2} - 4}$ ，其中a=3．

查看试题解析
19. 如图， $A C$ 平分 $∠ D A B$ ，且 $∠ D A B + ∠ D = 180 °$ ，点 $E$ 在射线 $B C$ 上．若 $∠ B = 95 °$ ， $∠ C A D = 25 °$ ，求 $∠ D C A$ 和 $∠ D C E$ 的度数．

查看试题解析
20. 已知方程组 ${\begin{cases} a x + 5 y = 15 ①, \\ 4 x + b y = - 2 ②, \end{cases}$
由于甲看错了方程①中的a，得到方程组的解为 ${\begin{cases} x = - 3, \\ y = - 1. \end{cases}$ 乙看错了方程②中的b，得到方程组的解为 ${\begin{cases} x = 5, \\ y = 2. \end{cases}$ 试求出a，b的值.

查看试题解析
21. 大马和小马驮着货物在途中有一段对话，如下图．
大马说：“我驮的东西给你一包多好哇！这样咱俩驮的包数就一样多了．”
小马说：“我还想给你1包呢！”
大马说：“那可不行！如果你给我1包，我驮的包数就是你的2倍了．”
根据大马和小马的对话，请你求出大马和小马各驮了几包货物?

查看试题解析
22. 仔细阅读下面例题．解答问题：
例题：已知二次三项式，x²-4x+m分解因式后有一个因式是(x+3)．求另一个因式以及m的值．

解：方法：设另一个因式为(x+n)，得x²-4x+m=(x+3)(x+n)．则x²-4x+m=x²+(n+3)x+3n，∴ ${\begin{matrix} n + 3 = - 4 \\ 3 n = m \end{matrix}$ ，解得 ${\begin{matrix} n = - 7 \\ m = - 21 \end{matrix}$ ，∴另一个因式为(x-7)，m的值为-21.

仿照以上方法解答：已知二次三项式8x²-14x-a分解因式后有一个因式是(2x-3)．求另一个因式以及a的值．

查看试题解析
23.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制，规定每天完成作业时间不超过1.5小时．该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查，并绘制出频数分布表和频数分布直方图的一部分．
时间（小时）
频数（人数）
频率
0≤t＜0.5
4
0.1
0.5≤t＜1
a
0.3
1≤t＜1.5
10
0.25
1.5≤t＜2
8
b
2≤t＜2.5
6
0.15
合计

1
（1）在表格中，a，b的值是多少？
（2）补全频数分布直方图；
（3）请估计该校1400名初中学生中，约有多少学生在1.5小时以内完成了家庭作业．

查看试题解析
24. 若 $x$ 满足 $(x - 4) (x - 9) = 6$ ，求 ${(x - 4)}^{2} + {(x - 9)}^{2}$ 的值．阅读下面求解的方法：
解：设 $x - 4 = a$ ， $x - 9 = b$ ，则 $a - b = (x - 4) - (x - 9) = 5$ ，
∵ $(x - 4) (x - 9) = 6$ ，
∴ $a b = 6$ ，
∴ ${(x - 4)}^{2} + {(x - 9)}^{2} = a^{2} + b^{2} = {(a - b)}^{2} + 2 a b = 5^{2} + 2 \times 6 = 37$ ．
请仿照上面的方法求解下面的问题：

(1)、若 $x$ 满足 $(x - 2) (x - 5) = 10$ ，求 ${(x - 2)}^{2} + {(x - 5)}^{2}$ 的值；

(2)、如图，正方形 $A B C D$ 中， $E$ 、 $F$ 分别是 $A D$ 、 $D C$ 上的点，且 $A E = 1$ ， $C F = 3$ ，长方形 $E M F D$ 的面积是 $15$ ，分别以 $M F$ 、 $D F$ 为边作正方形，若 $A D = x$ ，则① $D E =$ ， $D F =$ （用含 $x$ 的代数式表示）；②直接写出图中阴影部分的面积．

查看试题解析

时间（小时）	频数（人数）	频率
0≤t＜0.5	4	0.1
0.5≤t＜1	a	0.3
1≤t＜1.5	10	0.25
1.5≤t＜2	8	b
2≤t＜2.5	6	0.15
合计		1