浙江省2023年八年级下学期期末复习满分冲刺之特殊平行四边形
试卷更新日期:2023-05-26 类型:复习试卷
一、选择题(每小题3分,10小题,共30分)
-
1. 如图,点E为菱形的边BC上一点,且 , 连接与对角线相交于点F.已知 , 则的长为( )
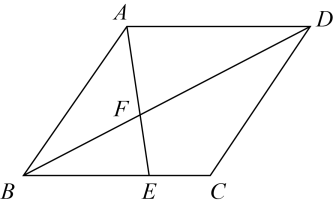 A、4 B、5 C、6 D、82. 下列说法错误的是( )A、对角线互相平分的四边形是平行四边形 B、四个角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、对角线垂直且相等的四边形是正方形3. 如图所示,一副三角尺摆放置在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若 ,则 等于( )
A、4 B、5 C、6 D、82. 下列说法错误的是( )A、对角线互相平分的四边形是平行四边形 B、四个角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、对角线垂直且相等的四边形是正方形3. 如图所示,一副三角尺摆放置在矩形纸片的内部,三角形的三个顶点恰好在矩形的边上,若 ,则 等于( )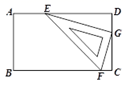 A、 B、 C、 D、4. 如图,某学校门口的伸缩门在伸缩的过程中,四边形始终是菱形,则下列结论不一定正确的是( )
A、 B、 C、 D、4. 如图,某学校门口的伸缩门在伸缩的过程中,四边形始终是菱形,则下列结论不一定正确的是( ) A、 B、 C、AB=AD D、AB=CD5. 如图,在菱形中,点E在的延长线上, , , , 求的长( )
A、 B、 C、AB=AD D、AB=CD5. 如图,在菱形中,点E在的延长线上, , , , 求的长( )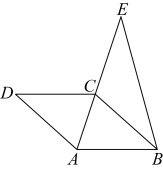 A、5 B、6 C、 D、6. 如图,是矩形的边上一个动点,矩形的两条边、的长分别为3和4,那么点到矩形的两条对角线和的距离之和是( )
A、5 B、6 C、 D、6. 如图,是矩形的边上一个动点,矩形的两条边、的长分别为3和4,那么点到矩形的两条对角线和的距离之和是( ) A、 B、 C、 D、7. 如图,一个边长分别为3cm、4cm、5cm的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是( )
A、 B、 C、 D、7. 如图,一个边长分别为3cm、4cm、5cm的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是( ) A、 B、 C、 D、8. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( )
A、 B、 C、 D、8. 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4 , 以下判断,其中不正确的是( ) A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S49. 如图,在正方形中,点E,F分别在边 , 上,且 , 作于点H,交于点G.若 , , 则的长为( ).
A、PA+PB+PC+PD的最小值为10 B、若△PAB≌△PCD,则△PAD≌△PBC C、若△PAB∼△PDA,则PA=2 D、若S1=S2 , 则S3=S49. 如图,在正方形中,点E,F分别在边 , 上,且 , 作于点H,交于点G.若 , , 则的长为( ). A、4 B、3 C、2 D、110. 如图,在长方形中, , 其内部有两个正方形 , 如图放置,且这两个正方形的边长之和为4.5,两个正方形相交于点K,L,连接 , 四边形的面积是2.5,则正方形的边长为( )
A、4 B、3 C、2 D、110. 如图,在长方形中, , 其内部有两个正方形 , 如图放置,且这两个正方形的边长之和为4.5,两个正方形相交于点K,L,连接 , 四边形的面积是2.5,则正方形的边长为( ) A、2 B、2.2 C、 D、2.5
A、2 B、2.2 C、 D、2.5二、填空题(每小题4分,6小题,共24分)
-
11. 已知菱形的两条对角线 , 则菱形的边长 .12. 如图,在正方形中,点E,F分别在边上, , , 则 .
 13. 如图,把矩形纸片沿对角线折叠,若 , , 则的面积是 .
13. 如图,把矩形纸片沿对角线折叠,若 , , 则的面积是 . 14. 如图,在矩形中, , 将沿翻折,使点B落在处,为折痕,再将沿翻折,使点C恰好落在线段上的点处,为折痕,连接 , 若 , 则度, .
14. 如图,在矩形中, , 将沿翻折,使点B落在处,为折痕,再将沿翻折,使点C恰好落在线段上的点处,为折痕,连接 , 若 , 则度, . 15. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 .
15. 如图,在正方形内部作等边 , 交于F点,过E作 , 分别交于点G,H.则的值是 . 16. 如图,矩形中, , , 是对角线上的两个动点,分别从同时出发,相向而行,速度均为 , 运动时间为秒,若分别是的中点,且 , 当为顶点的四边形为矩形时,的值为 .
16. 如图,矩形中, , , 是对角线上的两个动点,分别从同时出发,相向而行,速度均为 , 运动时间为秒,若分别是的中点,且 , 当为顶点的四边形为矩形时,的值为 .
三、解答题(共8题,共46分)
-
17. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
现有一个四边形木块,且∠A为直角,现要利用这块木块截一个正方形ABCD , 使其对角线长等于已知线段a . 请在图中作出这个正方形.

 18. 如图,已知正方形的边长为4,为中点,为上的一点,且 , 求证: .
18. 如图,已知正方形的边长为4,为中点,为上的一点,且 , 求证: . 19. 图1,图2都是由边长为1的正方形构成的网格,每个小正方形的顶点称为格点,线段的端点均在格点上,分别按要求画出图形.
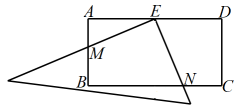
19. 图1,图2都是由边长为1的正方形构成的网格,每个小正方形的顶点称为格点,线段的端点均在格点上,分别按要求画出图形. (1)、在图1中画出等腰直角三角形 , 点C在格点上.(2)、在图2中画出以为边的菱形 , 点D,E在格点上.20. 如图,在平行四边形ABCD中, , 垂足分别为M,N.求证:四边形BNDM是矩形.
(1)、在图1中画出等腰直角三角形 , 点C在格点上.(2)、在图2中画出以为边的菱形 , 点D,E在格点上.20. 如图,在平行四边形ABCD中, , 垂足分别为M,N.求证:四边形BNDM是矩形. 21. 如图,在矩形中, , , 点E是上一点,连接 , 将沿着折叠,恰好点B与在上的点F重合,求的长.
21. 如图,在矩形中, , , 点E是上一点,连接 , 将沿着折叠,恰好点B与在上的点F重合,求的长.