浙江省2023年八年级下学期期末复习满分冲刺之平行四边形
试卷更新日期:2023-05-26 类型:复习试卷
一、选择题(每小题3分,10小题,共30分)
-
1. 若一个n边形内角和为 , 则n的值为( )A、5 B、6 C、7 D、82. 中,E,F是对角线上不同的两点.下列条件中,不能得出四边形一定为平行四边形的是( )
 A、 B、 C、 D、3. 如图,中,是的平分线,则周长为( )
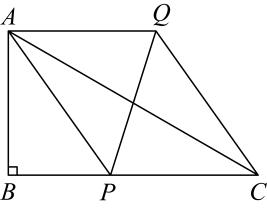
A、 B、 C、 D、3. 如图,中,是的平分线,则周长为( ) A、20 B、24 C、32 D、404. 如图,含角的三角尺()的长直角边与含角的三角尺()的斜边恰好重合,交于点E.P,Q分别是边 , 上的动点,当四边形为平行四边形时,的面积3,则线段的长是( )
A、20 B、24 C、32 D、404. 如图,含角的三角尺()的长直角边与含角的三角尺()的斜边恰好重合,交于点E.P,Q分别是边 , 上的动点,当四边形为平行四边形时,的面积3,则线段的长是( ) A、 B、 C、3 D、5. 已知中, , F是的中点,作 , 垂足E在线段上,不与点C重合,连接 , 下列结论:①;②;③;④中一定成立的是( )
A、 B、 C、3 D、5. 已知中, , F是的中点,作 , 垂足E在线段上,不与点C重合,连接 , 下列结论:①;②;③;④中一定成立的是( ) A、①②④ B、①③④ C、①②③ D、①②③④6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( )
A、①②④ B、①③④ C、①②③ D、①②③④6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( ) A、24 B、17 C、13 D、107. 如图,的对角线 , 相交于点O,下列等式一定正确的是( )
A、24 B、17 C、13 D、107. 如图,的对角线 , 相交于点O,下列等式一定正确的是( ) A、 B、 C、 D、8. 如图,在中,连接 , , , 则的度数是( )
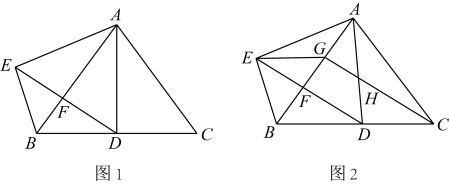
A、 B、 C、 D、8. 如图,在中,连接 , , , 则的度数是( )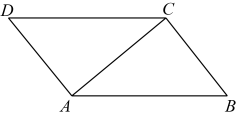 A、 B、 C、 D、9. 在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列结论不一定成立的是 ( )A、 AD=BC B、AB∥CD C、∠DAB=∠BCD D、∠DAB=∠ABC10. 如图,在▱ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M, 过点D作DN⊥AB于点N,且DN=6 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( )
A、 B、 C、 D、9. 在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列结论不一定成立的是 ( )A、 AD=BC B、AB∥CD C、∠DAB=∠BCD D、∠DAB=∠ABC10. 如图,在▱ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M, 过点D作DN⊥AB于点N,且DN=6 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( ) A、8 B、10 C、 D、
A、8 B、10 C、 D、二、填空题(每小题4分,6小题,共24分)
-
11. 如图,在中, , , . 点P为边上任意一点,连结 , 以 , 为邻边作 , 连结 , 则的最小值为 .
 12. 如图,在四边形ABCD中,CD=1,AB=2BC= , 且∠ABC+∠BCD=225°,则四边形ABCD周长的最大值为 .
12. 如图,在四边形ABCD中,CD=1,AB=2BC= , 且∠ABC+∠BCD=225°,则四边形ABCD周长的最大值为 . 13. 如图,将平行四边形沿对折,使点落在点处,若 , , , 则的长为 .
13. 如图,将平行四边形沿对折,使点落在点处,若 , , , 则的长为 .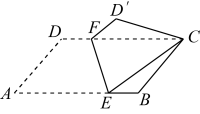 14. 如图,在平行四边形中,对角线交于点O, , 点E,F,G分别是的中点,交于点H.有下列4个结论:①;②;③;④ , 其中说法正确的是 .
14. 如图,在平行四边形中,对角线交于点O, , 点E,F,G分别是的中点,交于点H.有下列4个结论:①;②;③;④ , 其中说法正确的是 . 15. 如果一个多边形的内角和与外角和相等,那么这个多边形的边数是 .16. 如图,在中, , , , N是BC边上一点,M为AB边上的动点,D,E分别为CN,MN的中点,则DE的最小值是.
15. 如果一个多边形的内角和与外角和相等,那么这个多边形的边数是 .16. 如图,在中, , , , N是BC边上一点,M为AB边上的动点,D,E分别为CN,MN的中点,则DE的最小值是.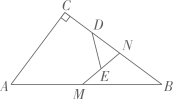
三、解答题(第17~22题每小题5分,第23、24题每小题8分)
-
17. 如图,在中,为边的中点,请用尺规作图法求作线段 , 使得点E在上, , 且.(保留作图痕迹,不写作法)
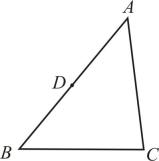 18. 如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
18. 如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长. 19. 如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
19. 如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF. 20. 如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.
20. 如图,点M、N在▱ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.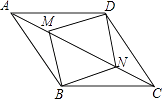 21. 分别在图①、图②中按要求作图(保留作图痕迹,不写作法).
21. 分别在图①、图②中按要求作图(保留作图痕迹,不写作法). (1)、如图①,在的方格纸中,点都在格点上,在图①中找一个格点D,使以点为顶点的四边形是平行四边形;(2)、如图②,已知四边形是平行四边形,为对角线,点P为上任意一点,请仅用无刻度的直尺在上找出另一点Q,使 .
(1)、如图①,在的方格纸中,点都在格点上,在图①中找一个格点D,使以点为顶点的四边形是平行四边形;(2)、如图②,已知四边形是平行四边形,为对角线,点P为上任意一点,请仅用无刻度的直尺在上找出另一点Q,使 .