人教版八年级下数学期末复习知识点扫盲满分计划——19.2.2一次函数
试卷更新日期:2023-05-26 类型:复习试卷
一、根据一次函数的定义求参数
-
1. 函数是关于的一次函数,则满足的条件是.2. 已知点都在直线上,则mn.(填大小关系)3. 若函数y=2x+3与y=3x-2b的图象交x轴于同一点,则b的值为 .4. 在平面直角坐标系中,若一次函数的图象过点 , , 则m的值为 .5. 直线经过 , 则;
二、列一次函数的解析式并求值
-
6. 一棵树现在的高度为 , 且未来10年内会每年长高 , 设年后树的高度为 , 则与的函数关系式( )A、 B、 C、 D、7. 山西老陈醋是中国四大名醋之一,已有3000余年的历史,素有“天下第一醋”的盛誉,以色、香、醇、浓、酸五大特征著称于世.某粮油店销售一种山西老陈醋,标价每瓶70元(10斤装),店里有个团购优惠,团购老陈醋5瓶以上,超过部分可享受8折优惠,若康康和朋友一起团购了x(x>5)瓶老陈醋共付款y元,则y与x的函数关系式为 .
 8. 已知池中有的水,每小时抽 , 则剩余水的体积与时间的函数关系式是 . (写出自变量取值范围)9. 某油箱容量为60升的汽车,加满汽油后行驶了100千米时,油箱中的汽油大约消耗了12升,如果加满汽油后汽车行驶的路程为x(千米),油箱中剩余油量为y(升),则y与x之间的关系式是 .10. 某经销商销售了一种水果,根据以往销售经验,每天的售价与销售量之间有如下关系:
8. 已知池中有的水,每小时抽 , 则剩余水的体积与时间的函数关系式是 . (写出自变量取值范围)9. 某油箱容量为60升的汽车,加满汽油后行驶了100千米时,油箱中的汽油大约消耗了12升,如果加满汽油后汽车行驶的路程为x(千米),油箱中剩余油量为y(升),则y与x之间的关系式是 .10. 某经销商销售了一种水果,根据以往销售经验,每天的售价与销售量之间有如下关系:每千克售价(元)
38
37
36
35
…
20
每天销量(千克)
50
52
54
56
…
86
(1)、从表格可以看出售价每下调1元销售量就增加千克;(2)、若某天的销售价定为30元/千克,这天的销量为千克;如果这种水果的进价是20元/千克,销售利润是元.(3)、设当售价从38元/千克下调到售价为x元/千克时,每天销售量为y千克,直接写出y与x之间的关系式 .三、判断一次函数的图像
-
11. 一次函数的图象大致是( )A、
 B、
B、 C、
C、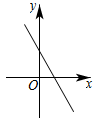 D、
D、 12. 在如图所示的计算程序中,y与x之间的函数关系式所对应的图象是( )
12. 在如图所示的计算程序中,y与x之间的函数关系式所对应的图象是( ) A、
A、 B、
B、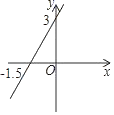 C、
C、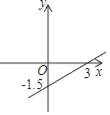 D、
D、 13. 如图所示,点B,C分别在y=2x和y=kx-2a上,A,D为x轴上两点,点B的纵坐标为a,若四边形ABCD为矩形,且 , 则k的值为( )
13. 如图所示,点B,C分别在y=2x和y=kx-2a上,A,D为x轴上两点,点B的纵坐标为a,若四边形ABCD为矩形,且 , 则k的值为( ) A、 B、 C、 D、14. 已知一次函数y=kx+b的图象如图所示,当x≤0时,y的取值范围是( )
A、 B、 C、 D、14. 已知一次函数y=kx+b的图象如图所示,当x≤0时,y的取值范围是( )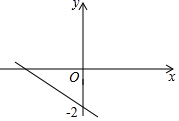 A、y≥0 B、y≤0 C、﹣2≤y<0 D、y≥﹣215. 在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A、y≥0 B、y≤0 C、﹣2≤y<0 D、y≥﹣215. 在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( ) A、
A、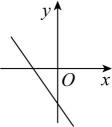 B、
B、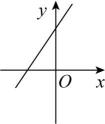 C、
C、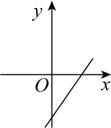 D、
D、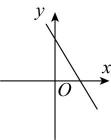
四、一次函数图像与坐标交点问题
-
16. 直线与x轴的交点坐标是( ).A、 B、 C、 D、17. 如图,在平面直角坐标系中,过点 , 分别作x轴的垂线,垂足分别为A、B.
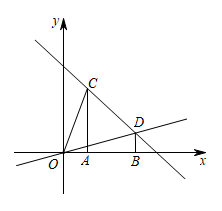 (1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.
(1)、求直线CD和直线OD的解析式;(2)、点M为直线OD上的一个动点,过点M作x轴的垂线交x轴于点P,交直线CD于点N.①当PM为中位线时,求MN的长;
②是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由.
18. 把直线向上平移5个单位长度,平移后的直线与x轴的交点坐标为 .19. 如图所示,在平面直角坐标系中,已知一次函数的图象与轴,轴分别交于 , 两点,以为边在第二象限内作正方形 . (1)、求正方形的面积;(2)、求点 , 的坐标;(3)、在轴上是否存在点 , 使的周长最小?若存在,请求出点的坐标;若不存在,请说明理由.20. 如图,直线与x轴相交于点A,与y轴相交于点B.
(1)、求正方形的面积;(2)、求点 , 的坐标;(3)、在轴上是否存在点 , 使的周长最小?若存在,请求出点的坐标;若不存在,请说明理由.20. 如图,直线与x轴相交于点A,与y轴相交于点B. (1)、求A,B两点的坐标;(2)、过B点作直线与x轴交于点P,若△ABP的面积为5,试求点P的坐标.
(1)、求A,B两点的坐标;(2)、过B点作直线与x轴交于点P,若△ABP的面积为5,试求点P的坐标.五、一次函数的平移问题
-
21. 直线是由( )单位长度得到的.A、向右平移8个 B、向左平移8个 C、向下平移8个 D、向上平移8个22. 将直线向左平移()个单位长度后,经过点 , 则的值为 .23. 如图,直线与x轴,y轴分别交于点A,B,将直线向左平移得到一条新的直线,它与x轴,y轴分别交于点C,D.若 , 则(1)、点D的坐标是;(2)、直线CD的解析式为 .
 24. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为 .25. 已知直线l:y=2x+4,把直线l向右平移6个单位得到直线l1 , 则直线l1的表达式为( )A、 B、 C、 D、
24. 若一次函数的图象向下平移3个单位后经过点 , 则b的值为 .25. 已知直线l:y=2x+4,把直线l向右平移6个单位得到直线l1 , 则直线l1的表达式为( )A、 B、 C、 D、六、利用一次函数的增减性
-
26. 已知点都在直线上,则m,n的大小关系是( )A、 B、m=n C、m<n D、不能确定27. 已知一次函数的图象上两点 , , 当时,有 , 那么m的值可能是( ).A、 B、 C、 D、28. 已知,一次函数 , 当时, . 则的值是 .29. 一次函数的图象经过两个点和 , 则 , 的大小关系是( )A、 B、 C、当时, D、当时,30. 若点 , 都在直线上,则下列大小关系成立的是( ).A、 B、 C、 D、
七、一次函数的规律探究
-
31. 如图,在平面直角坐标系中,直线l与x轴交于点B1 , 与y轴交点于D,且OB1=1,∠ODB1=60°,以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , ……依次进行下去,则点A2020的横坐标是.
 32. 如图,直线与轴交于点D,与轴交于点 , 把正方形、和按如图所示方式放置,点、在直线上,点、、在轴上,按照这样的规律,则点的坐标是 , 正方形中的点的坐标为 .
32. 如图,直线与轴交于点D,与轴交于点 , 把正方形、和按如图所示方式放置,点、在直线上,点、、在轴上,按照这样的规律,则点的坐标是 , 正方形中的点的坐标为 . 33. 如图放置的△OAB1 , △B1A1B2 , OB2A2B3都是边长为2的等边三角形,边0A在y轴上,点B1 , B2 , B3 , ……都在直线y=x上,则点A2022的坐标是
33. 如图放置的△OAB1 , △B1A1B2 , OB2A2B3都是边长为2的等边三角形,边0A在y轴上,点B1 , B2 , B3 , ……都在直线y=x上,则点A2022的坐标是 34. 如图,△OA1B1 , △A1A2B2都是斜边在x轴上的等腰直角三角形,点A1 , A2都在x轴上,点B1 , B2都在一次函数的图象上,则点B2的坐标为 .
34. 如图,△OA1B1 , △A1A2B2都是斜边在x轴上的等腰直角三角形,点A1 , A2都在x轴上,点B1 , B2都在一次函数的图象上,则点B2的坐标为 . 35. 如图,在平面直角坐标系中,将沿x轴向右滚动到的位置,再到的位置…依次进行下去,若已知点 , 则点的坐标为.
35. 如图,在平面直角坐标系中,将沿x轴向右滚动到的位置,再到的位置…依次进行下去,若已知点 , 则点的坐标为.
八、综合训练
-
36. 如图1,在平面直角坐标系中,直线:与坐标轴交于 , 两点,点为的中点,动点从点出发,沿方向以每秒1个单位的速度向终点运动,同时动点从点出发,以每秒2个单位的速度沿射线方向运动,当点到达点时,点也停止运动以 , 为邻边构造▱ , 设点运动的时间为秒.
 (1)、直接写出点的坐标为 .(2)、如图2,过点作轴于 , 过点作轴于证明:≌ .(3)、如图3,连结 , 当点恰好落在的边所在的直线上时,求所有满足要求的的值.37. 如图,在平面直角坐标系中,直线y=-x+8分别交两坐标轴于点A、B,直线CD与直线AB交于点C,与x轴交于点D.点C的横坐标为4,点D在线段OA上,且AD=7.
(1)、直接写出点的坐标为 .(2)、如图2,过点作轴于 , 过点作轴于证明:≌ .(3)、如图3,连结 , 当点恰好落在的边所在的直线上时,求所有满足要求的的值.37. 如图,在平面直角坐标系中,直线y=-x+8分别交两坐标轴于点A、B,直线CD与直线AB交于点C,与x轴交于点D.点C的横坐标为4,点D在线段OA上,且AD=7.
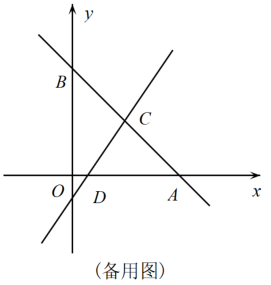
 (1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.38. 设 , 关于x的一次函数 , 当时,y的最小值是( )A、 B、 C、k D、39. 已知关于x的一次函数为 , 下列说法中错误的是( )A、若函数图象经过原点,则 B、若 , 则函数图象经过第一、二、三象限 C、函数图象与y轴交于点 D、无论m为何实数,函数图象总经过40. 如图,已知一次函数的图象经过 , 两点,并且交x轴于点C,交y轴于点D.
(1)、C、D两点的坐标分别为;(2)、求直线CD的函数解析式;(3)、在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.38. 设 , 关于x的一次函数 , 当时,y的最小值是( )A、 B、 C、k D、39. 已知关于x的一次函数为 , 下列说法中错误的是( )A、若函数图象经过原点,则 B、若 , 则函数图象经过第一、二、三象限 C、函数图象与y轴交于点 D、无论m为何实数,函数图象总经过40. 如图,已知一次函数的图象经过 , 两点,并且交x轴于点C,交y轴于点D. (1)、求k和m的值;(2)、求的面积.41. 如图,一次函数与x轴,y轴分别交于点A,B,点是直线AB上一点,直线MC交x轴于点;
(1)、求k和m的值;(2)、求的面积.41. 如图,一次函数与x轴,y轴分别交于点A,B,点是直线AB上一点,直线MC交x轴于点;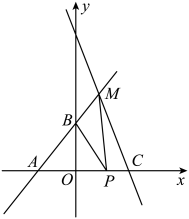 (1)、求直线MC的函数解析式;(2)、若点P是线段AC上一动点,连接BP,MP,若的面积是面积的2倍,求P点坐标.42. 如图,直线l1:y1=-2x+6与x轴,y轴分别交于点A,B,直线l2过点C(-5,0),与直线l1交于点D(a,8),与y轴交于点E.
(1)、求直线MC的函数解析式;(2)、若点P是线段AC上一动点,连接BP,MP,若的面积是面积的2倍,求P点坐标.42. 如图,直线l1:y1=-2x+6与x轴,y轴分别交于点A,B,直线l2过点C(-5,0),与直线l1交于点D(a,8),与y轴交于点E. (1)、求直线l2的解析式;(2)、求△BDE的面积.43. 在一次函数的图象上有一点 , 已知点到轴的距离为 , 则点的坐标为 .44. 已知一次函数(k为常数,且),无论k取何值,该函数的图象总经过一个定点,则这个定点的坐标是( )A、(0,1) B、(2,1) C、(1,0) D、(1,2)45. 对任意实数a,直线y=(a−1)x+3−2a一定经过点( )A、 B、 C、 D、
(1)、求直线l2的解析式;(2)、求△BDE的面积.43. 在一次函数的图象上有一点 , 已知点到轴的距离为 , 则点的坐标为 .44. 已知一次函数(k为常数,且),无论k取何值,该函数的图象总经过一个定点,则这个定点的坐标是( )A、(0,1) B、(2,1) C、(1,0) D、(1,2)45. 对任意实数a,直线y=(a−1)x+3−2a一定经过点( )A、 B、 C、 D、