人教版八年级下数学期末复习知识点扫盲满分计划——19.1.1正比例函数
试卷更新日期:2023-05-26 类型:复习试卷
一、正比例函数的定义
-
1. 若 为y关于x的正比例函数,则m的值为.2. 下列问题中,两个变量之间是正比例函数关系的是( )A、汽车以 的速度匀速行驶,行驶路程 与行驶时间 之间的关系 B、圆的面积 与它的半径 之间的关系 C、某水池有水 ,现打开进水管进水,进水速度 , 后水池有水 D、有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系3. 若函数y=2x+(1-m)是正比例函数,则m的值是。4. 已知y=(k-3)x+ -9是关于x的正比例函数,求当x=-4时,y的值.5. 若函数y=(m﹣1)x|m|是正比例函数,则该函数的图象经过第象限.
二、正比例函数的图像
-
6. 如图,点B,C分别在直线y=2x和直线y=kx上,A、D是x轴上两点,若四边形ABCD是长方形,且AB:AD=1:3,则k的值为.
 7. 如图,三个正比例函数的图象分别对应的解析式是:①y=ax , ②y=bx , ③y=cx , 请用“>”表示a , b , c的不等关系是 .
7. 如图,三个正比例函数的图象分别对应的解析式是:①y=ax , ②y=bx , ③y=cx , 请用“>”表示a , b , c的不等关系是 . 8. 正比例函数y=(m2+1)x经过的象限是( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限9. 如图,点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为.
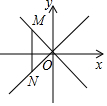
8. 正比例函数y=(m2+1)x经过的象限是( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限9. 如图,点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为.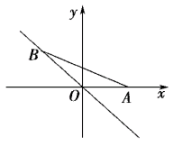 10. 已知▱ABCD中,A(1,3),B(2,-1),C(5,-5)(1)、D的坐标为.(2)、若经过原点的一条直线平分▱ABCD的面积,求此直线的解析式
10. 已知▱ABCD中,A(1,3),B(2,-1),C(5,-5)(1)、D的坐标为.(2)、若经过原点的一条直线平分▱ABCD的面积,求此直线的解析式三、正比例函数的性质
-
11. 已知点和点都在正比例函数的图象上.请你写出一个符合条件的k值 (写出一个即可),使当x1<x2时,y1>y2 .12. 对于函数 , 下列结论错误的是( )A、函数图象必经过点(1,3) B、y的值随x值的增大而增大 C、当时, D、函数图象经过第三象限13. 若正比例函数图象过点(1,-2),则下列说法不正确的是( )A、函数值随自变量的增大而增大 B、函数值随自变量的增大而减小 C、函数图象过点(2,-4) D、函数图象过二、四象限14. 在函数y=kx(k>0)的图象上有三点A1(x1 , y1),A2(x2 , y2),A3(x3 , y3),已知x1<x2<0<x3 , 则下列各式中正确的是( )A、y1<y2<0<y3 B、y3<0<y1<y2 C、y2<y1<y3<0 D、y3<y1<0<y215. 关于函数 , 下列结论正确的是( )A、函数图象必经过点(1,2) B、函数图象经过第二、四象限 C、y随x的增大而增大 D、不论x取何值,总有y>0
四、利用正比例函数求解析式
-
16. 已知y与x-1成正比例,当x=4时,y=27,求:(1)、y与x的函数解析式;(2)、当y=12时,求x的值.17. 已知 与 成正比例,且当 时, .(1)、求 与 的函数关系式;(2)、判断点 是否在该函数的图象上.18. 已知y与2x﹣3成正比例,且当x=1时,y=﹣1.(1)、求y关于x的函数解析式;(2)、当y=1时,求x的值.19. 已知y﹣1与x﹣1成正比例,且x=3时,y=4.(1)、求y与x之间的函数关系式;(2)、当y=﹣1时,求x的值.20. 已知 与 成正比例,当 时, .(1)、求 与 的函数关系式;(2)、若 在此函数图象上,求 的值.
五、综合训练
-
21. 已知正比例函数的图象经过点 , 如果和在该函数的图象上,那么a和b的大小关系是( )A、 B、 C、 D、22. 在平面直角坐标中,点A(﹣3,2)、B(﹣1,2),直线y=kx(k≠0)与线段AB有交点,则k的取值范围为 .23. 如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为 .
 24. 已知P1(x1 , y1),P2(x2 , y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,如果P1点在P2点左边,那么y1 , y2的大小关系是( )A、y1=y2 B、y1<y2 C、y1>y2 D、不能确定25. 已知y+5与3x+4成正比例,当x=1时,y=2.求:(1)、y与x之间的函数表达式;(2)、当x=-1时,求y的值.26. 若函数 的图象经过A(1, )、B(-1, )、C(-2, )三点,则 , , 的大小关系是.27. 已知正比例函数 ,当 时,对应的y的取值范围是 ,且y随x的减小而减小,则k的值为 .28. 若y+1与x-2成正比例,当 时, ;则当 时, 的值是( )A、-2 B、-1 C、0 D、129. 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
24. 已知P1(x1 , y1),P2(x2 , y2)是正比例函数y=kx(k≠0)在第二象限的图象上的两个点,如果P1点在P2点左边,那么y1 , y2的大小关系是( )A、y1=y2 B、y1<y2 C、y1>y2 D、不能确定25. 已知y+5与3x+4成正比例,当x=1时,y=2.求:(1)、y与x之间的函数表达式;(2)、当x=-1时,求y的值.26. 若函数 的图象经过A(1, )、B(-1, )、C(-2, )三点,则 , , 的大小关系是.27. 已知正比例函数 ,当 时,对应的y的取值范围是 ,且y随x的减小而减小,则k的值为 .28. 若y+1与x-2成正比例,当 时, ;则当 时, 的值是( )A、-2 B、-1 C、0 D、129. 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( ) A、k≤2 B、 C、 D、30. 若y=(m﹣1)x|m|是正比例函数,则m的值为31. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l2于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .
A、k≤2 B、 C、 D、30. 若y=(m﹣1)x|m|是正比例函数,则m的值为31. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l2于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .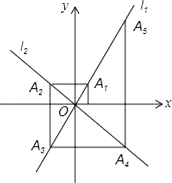 32. 已知函数y=(k﹣) .(1)、k为何值时,函数是正比例函数;(2)、k为何值时,正比例函数的图象在二,四象限;(3)、k为何值时,正比例函数y随x的减小而减小.33. 已知y关于x的函数y=(m+)(n﹣1)x|n|+m2﹣是正比例函数.(1)、求m,n的值;
32. 已知函数y=(k﹣) .(1)、k为何值时,函数是正比例函数;(2)、k为何值时,正比例函数的图象在二,四象限;(3)、k为何值时,正比例函数y随x的减小而减小.33. 已知y关于x的函数y=(m+)(n﹣1)x|n|+m2﹣是正比例函数.(1)、求m,n的值;
(2)、根据两点法画出函数图象;(3)、根据正比例函数的性质写出即可.
34. 已知直线L1:y=4x和点P(6,4),在直线L1上求一点Q,使过P,Q的直线与直线L1以及x轴在第一象限内所围成的三角形面积最小.35. 下列函数解析式中,不是正比例函数的是( )A、xy=﹣2 B、y+8x=0 C、3x=4y D、