初中数学同步训练必刷题（人教版七年级下册 10.3 课题学习从数据谈节水）
试卷更新日期：2023-05-25 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 自主创业的小华开了一家特色美食店，开业一周后地计划用统计图直观反成这周各天收入的起伏情况，下列各统计图中，你认为最优的选择是（ ）A、统计数据表 B、条形统计图 C、扇形统计图 D、折线统计图2. 如图表示某校学生参加第二课堂活动情况统计，其中唱歌的人数占20%，表示书法的扇形的圆心角60°，书法和绘画的人数比为1：2，则参加其它活动的人数占总人数的（ ）
A、35% B、30% C、25% D、20%3. 李老师对本班50名学生的血型进行了统计，列出如下的统计表：组别
A型
B型
型
O型
占全班人数的百分比
40%
30%
20%
10%
则本班型血的人数是（ ）
A、20 B、15 C、5 D、104. 为节约用电，某市根据每户居民每月用电量分为三档频数户收费．第一档电价：每月用电量低于240度，每度0.48元；第二档电价：每月用电量为度，每度0.53元；第三档电价：每月用电量超过400度，每度0.78元小明同学对该市有1000居民的某小区月用电量（单位：度）进行了抽样调查，绘制了如图所示的统计图．下列说法不合理的是
A、本次抽样调查的样本容量为50 B、估计该小区按第一档电价交费的居民户数最多 C、该小区按第二档电价交费的居民有240户 D、该小区按第三档电价交费的居民比例约为5. 从A地到B地有驾车、公交、地铁三种出行方式，为了选择适合的出行方式，对6：00—10：00时段这三种出行方式不同时刻出发所用时长（从A地到B地）进行调查、记录与整理，数据如图所示.
根据统计图提供的信息，下列推断合理的是（ ）
A、若7：00前出发，地铁是最快的出行方式 B、若选择公交出行且需要30分钟以内到达，则7：00之前出发均可 C、驾车出行所用时长受出发时刻影响较小 D、在此时段里，地铁出行的所用时长都在30分钟至40分钟之间6. 图（1）表示的是某书店今年1~4月的各月营业总额的情况，图（2）表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~4月的营业额一共是130万元，则这四个月中“党史”类书籍的营业额最高的是（ ）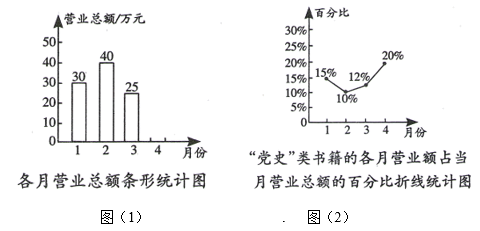
A、1月 B、2月 C、3月 D、4月7. 某学校将为初一学生开设A，B，C，D，E，F共6门选修课，现选取若干学生进行了“我最喜欢的一门选修课”调查，将调查结果绘制成如图统计图表(不完整).选修课
A
B
C
D
E
F
人数
40
60
100
根据图表提供的信息，下列结论中错误的是（ ）
A、这次被调查的学生人数为400人 B、扇形统计图中E部分扇形的圆心角为72° C、被调查的学生中喜欢选修课E，F的人数分别为80，70 D、喜欢选修课C的人数最少8. 随着智能手机的普及，“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐，某商场对2021年7—12月中使用这两种支付方式的情况进行统计，得到如图所示的折线图，根据统计图中的信息，得出以下四个推断，其中不合理的是（ ）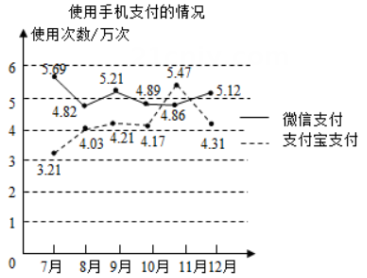
A、6个月中11月份使用手机支付的总次数最多 B、6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多 C、6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大 D、9月份平均每天使用手机支付的次数为0.314万次9. 某校八((1)斑全体同学喜欢的球类运动如图所示.则从图中可以直接看出（ ）
A、喜欢各种球类的具体人数 B、全班同学一学期来喜欢各种球类的变化情况 C、全班的总人数 D、全班同学现在喜欢各种球类人数的百分比10. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查.已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：身高情况分组表(单位：cm)
组别
A
B
C
D
E
身高
x＜155
155≤x＜160
160≤x＜165
165≤x＜170
x≥170
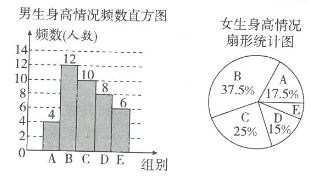
根据图表提供的信息，样本中，身高在160≤x＜170之间的女学生人数为（ ）
A、8 B、6 C、14 D、16二、填空题（每空3分，懂30分）
-
11. 空气是由多种气体混合而成的，为了简明扼要地介绍空气的组成情况，较好地描述数据，最适合使用的统计图是.12. 如图是某中学七年级学生视力统计图，其中近视200~400度的学生所在扇形的圆心角为度.
13. 某小区12月1日~12月5日每天用水量变化情况如图所示，该小区这5天一共用水立方米．
14. 某健步走运动爱好者用手机软件记录了某个月（30天）每天健步走的步数，并制成了如图所示的统计图.根据该图，在这个月中，他健步走的步数达到1.5万的天数是 .
15. 为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数.请根据统计表计算，跳绳次数（x）在120≤x＜200范围内人数占抽查学生总人数的百分比为.1分钟内跳绳的次数
人数
40≤x＜80
10
80≤x＜120
50
120≤x＜160
30
160≤x＜200
10
16. 在整理数据3，5，6，6，■，8时，发现面处的数据看不清，但从扇形统计图上发现数据6的圆心角是180°，则■处的数据是 ．17. 如图，整个圆表示某班参加课外活动的总人数，跳绳的人数占30%，表示踢毽的扇形圆心角是60°，踢毽和打篮球的人数比是12，那么表示参加“其它”活动的人数占总人数的%.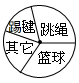
18. 公益活动中，小明根据本班同学的捐款情况绘制成如图所示的不完整统计图，其中捐10元的人数占全班总人数的40%，则本次捐款20元的人数为人.
19. 如图反映的是双十中学七（3）班学生外出方式（乘车、步行、骑车）人数的条形统计图（部分）和扇形分布图，那么扇形图中骑车的学生人数所占的圆心角是 °．
20. 某中学七年级甲.乙，丙三个班中，每班的学生人数都为40名，某次数学考试的成绩统计如下(如图，每组分数含最小值，不含最大值).根据图，表提供的信息﹐则80～90分这一组人数最多的班是.
丙班数学成绩频数统计表
分数
50～60
60～70
70～80
80～90
90～100
人数
1
4
15
11
9
三、解答题（共6题，共60分）
-
21. 暑期将至，学校组织学生进行“防溺水”安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．其中A组的频数a比B组的频数b小15．请根据以上信息，解答下列问题：
(1)、本次共抽取名学生，b的值为；(2)、在扇形统计图中，n= ， E组所占比例为%；(3)、补全频数分布直方图；(4)、若全校共有2500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．22. 随着科技的不断发展，越来越多的中学生拥有了自己的手机，某中学课外兴趣小组对使用手机的时间做了调查：随机抽取了该校部分使用手机的中学生进行调查（问卷调查表如图所示），并用调查结果绘制了图1、图2两种“周使用手机的时间统计图”（均不完整），请根据统计图表解答以下问题：中学生每周使用手机的时间问卷调查表：（在相应的时间段打√）
选项
使用时间t（小时）
A
B
C
D
(1)、本次接受问卷调查的共有人；在扇形统计图中“D”选项所占的百分比；(2)、扇形统计图中，“B”选项所对应扇形圆心角为度；(3)、请补全条形统计图；(4)、若该校共有1200名中学生，请你估计该校使用手机的时间在“A”选项的有多少名学生？23. 下面是某年参加国际教育评估的15个国家学生的数学平均成绩（）的统计图．
(1)、请你补全频数分布直方图；(2)、求所在扇形圆心角的度数（保留整数）；(3)、哪一个图能更好地说明一半以上国家的学生成绩在之间？(4)、哪一个图能更好地说明学生成绩在的国家多于成绩在的国家？24. 白色污染（White Pollution）是人们对难降解的塑料垃圾（多指塑料袋）污染环境现象的一种形象称谓．为了让全校同学感受丢弃塑料袋对环境的影响，小彬随机抽取某小区户居民，记录了这些家庭某个月丢弃塑料袋的数量（单位：个）：29 39 35 39 39 27 33 35 31 31 32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38 29 39 35 33 39 39 38 42 37 32
请根据上述数据，解答以下问题：
分组
划记
频数
A：25-30
____
____
B：30~35
14
C：35~40
____
____
D：40~45
4
合计
/
40
(1)、小彬按“组距为”列出了如下的频数分布表（每组数据含最小值），请将表中空缺的部分补充完整，并补全频数分布直方图；(2)、根据（1）中的直方图可以看出，这户居民家这个月丢弃塑料袋的个数在组的家庭最多；（填分组序号）(3)、根据频数分布表，小彬又画出了图所示的扇形统计图．请将统计图中各组占总数的百分比填在图中；(4)、若该小区共有户居民家庭，请你估计每月丢弃的塑料袋数量不小于个的家庭个数．25. 某学校体育兴趣小组，为了更好的开展活动，需要了解学校1000名学生对A ， B ， C ， D四项体育活动的喜好情况，随机抽取了100名学生进行了“你最喜欢哪种运动”的调查（必选且只选一种），根据调查绘制了条形统计图和扇形统计图，部分信息如下：
(1)、在抽取的100人中最喜欢运动项目A的人数为；(2)、求扇形统计图中“C”对应扇形的圆心角度数；(3)、补全条形统计图；(4)、依据本次调查结果，估计全校1000人名学生中最喜欢B运动项目的人数．26. 某校响应国家号召，为防疫做贡献，决定在全校范围内开展防疫知识的宣传教育活动．为了了解宣传效果，该校在活动前和活动后抽取同一部分学生，就防疫知识进行两次跟踪测评（测试满分100分），两次测评中所有同学的成绩没有低于30分．现在将收集的数据制成频数分布直方图（每一组包含左端值，不包含右端值）和频数分布表．
宣传活动后防疫知识情况统计表
成绩
频数
2
6
6
16
m
30
12
(1)、宣传活动前，在抽取的学生中哪一组成绩的人数最多？占抽取人数的百分之几？(2)、宣传活动后，在抽取的学生中分数高于65分的至少有人，至多有人；(3)、小红认为，宣传活动后成绩在60~70的人数为16，比活动前减少了14人，因此学校开展的宣传活动没有效果请你结合统计图表，说一说小红的看法是否正确．