天津市津南区七校联考2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 下列各数: , , , , (相邻两个之间的个数逐次加), , , 是无理数的有( )个.A、 B、 C、 D、2. 下列各式,正确的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点(﹣1,m2+1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知实数x,y满足+|y+3|=0,则x+y的值为 ( )A、-2 B、2 C、4 D、-45. 为了绿化校园,某班学生参与共种植了144棵树苗 其中男生每人种3棵,女生每人种2棵,且该班男生比女生多8人,设男生有 人,女生有 人,根据题意,所列方程组正确的是A、 B、 C、 D、6. 如图所示,小明家相对于学校的位置,下列描述最正确的是( )
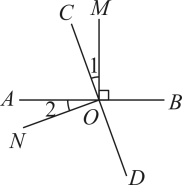
 A、在距离学校300米处 B、在学校的东南方向 C、在东偏南45°方向300米处 D、在学校北偏西45°方向300米处7. 如图,E是直线 上一点, ,射线 平分 , .则 ( )
A、在距离学校300米处 B、在学校的东南方向 C、在东偏南45°方向300米处 D、在学校北偏西45°方向300米处7. 如图,E是直线 上一点, ,射线 平分 , .则 ( ) A、 B、 C、 D、8. 已知轴,且点A的坐标为 , 点B的坐标为 , 则点A的坐标为( )A、 B、 C、 D、9. 若 是关于x,y的二元一次方程,则 ( )A、2 B、 C、2或 D、010. 下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.A、5个 B、4个 C、3个 D、2个11. 若 ,是关于 和 的二元一次方程 的解,则 的值等于A、3 B、6 C、 D、12. 实数、在数轴上的位置如图所示,化简的结果是( ).
A、 B、 C、 D、8. 已知轴,且点A的坐标为 , 点B的坐标为 , 则点A的坐标为( )A、 B、 C、 D、9. 若 是关于x,y的二元一次方程,则 ( )A、2 B、 C、2或 D、010. 下列语句中真命题有( )①点到直线的垂线段叫做点到直线的距离;②内错角相等;③两点之间线段最短;④过一点有且只有一条直线与已知直线平行;⑤在同一平面内,若两条直线都与第三条直线垂直,则这两条直线互相平行.A、5个 B、4个 C、3个 D、2个11. 若 ,是关于 和 的二元一次方程 的解,则 的值等于A、3 B、6 C、 D、12. 实数、在数轴上的位置如图所示,化简的结果是( ). A、 B、0 C、 D、
A、 B、0 C、 D、二、填空题
-
13. 把命题“同角的余角相等”写成“如果……,那么……”的形式为 .14. , , 则=15. 若一个正数的两个平方根分别是和 , 则这个正数是.16. 已知 是关于 的二元一次方程 的解,则17. 如图,已知 , 直线分别与 , 相交于 , 两点,现把一块含角的直角三角尺按如图所示的位置摆放.若 , 则 .
 18. 将从开始的连续自然数按下表所示规律排列:
18. 将从开始的连续自然数按下表所示规律排列:行
第列
第列
第列
第列
第行
第行
第行
第行
.
第行
规定位于第行、第列的自然数记为 .如:自然数记为 , 自然数记为 , 自然数记为 , , 按此规律,自然数记为 .
三、解答题
-
19. 计算:(1)、(2)、20. 解方程组:(1)、 ;(2)、 .21. 如图,在平面直角坐标系中,点、、的坐标分别为( , ),(4,3),( , 2).将先向左平移4个单位,再向下平移2个单位得到 .
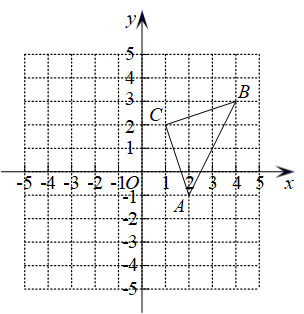 (1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;( , )( , )( , )(3)、求的面积.22. 完成下面的证明.
(1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;( , )( , )( , )(3)、求的面积.22. 完成下面的证明.如图,已知AD⊥BC,EF⊥BC,∠1=∠2,求证:∠BAC+∠AGD=180°.
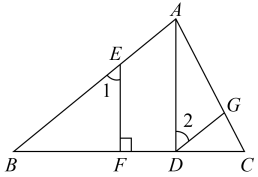
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=90°,∠ADB=90°( ),
∴∠EFB=∠ADB(等量代换),
∴EF//AD( ),
∴∠1=∠BAD( ),
又∵∠1=∠2(已知),
∴∠2=∠ ▲ (等量代换),
∴DG//BA( ),
∴∠BAC+∠AGD=180°( ).
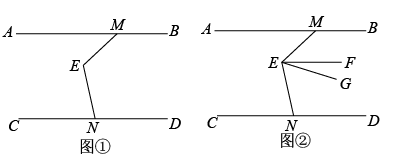
23. 如图,∠AGB=∠EHF,∠C=∠D,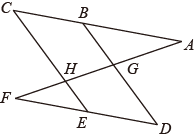 (1)、求证:BDCE;(2)、若∠A=30°,求∠F的度数.
(1)、求证:BDCE;(2)、若∠A=30°,求∠F的度数.