上海市闵行区2022-2023学年七年级下学期期中考试数学试题
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 在、、、、、、(位数是无限的,相邻两个“”之间“”的个数依次增加个)这些数中,无理数的个数是( )A、 B、 C、 D、2. 下列运算中,正确的是( )A、 B、 C、 D、3. 下列说法不正确的是( )A、两直线被第三条直线所截,所得的同位角相等 B、两平行线被第三条直线所截,一组内错角的角平分线互相平行 C、两平行线被第三条直线所截,一组同位角的角平分线互相平行 D、两平行线被第三条直线所截,一组同旁内角的角平分线互相垂直4. 如图,下列条件不能判定ABCD的是( )
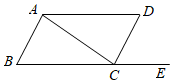 A、∠CAD=∠ACB B、∠BAC=∠ACD C、∠B+∠BCD=180° D、∠B=∠DCE5. 在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是( )A、锐角三角形 B、等腰三角形 C、直角三角形 D、等腰直角三角形6. 如图,在中, , 把沿边上的高所在的直线翻折,点落在边的延长线上的点处,如果 , 则的度数为( )
A、∠CAD=∠ACB B、∠BAC=∠ACD C、∠B+∠BCD=180° D、∠B=∠DCE5. 在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是( )A、锐角三角形 B、等腰三角形 C、直角三角形 D、等腰直角三角形6. 如图,在中, , 把沿边上的高所在的直线翻折,点落在边的延长线上的点处,如果 , 则的度数为( )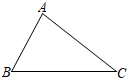 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
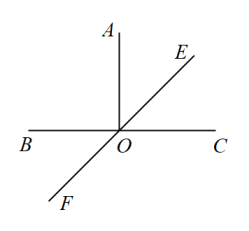
7. 的平方根是 .8. 计算: = .9. 比较大小: (填“>”或“<”或“=”).10. 把写成方根的形式: .11. 用科学记数法表示 . (保留两个有效数字)12. 如果 , 那么整数= .13. 已知数轴上点到原点的距离为1,且点A在原点的左侧,数轴上到点A的距离为的点所表示的数是 .14. 如图, , 直线平分 , 则 .
 15. 如图, , 、交于点 , 三角形的面积等于 , 三角形的面积等于 , 那么三角形的面积等于 .
15. 如图, , 、交于点 , 三角形的面积等于 , 三角形的面积等于 , 那么三角形的面积等于 .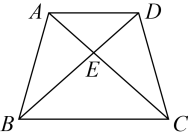 16. 如图, , , , 则 .
16. 如图, , , , 则 . 17. 一张长方形纸条经过折叠后如图所示, , 则∠1= .
17. 一张长方形纸条经过折叠后如图所示, , 则∠1= .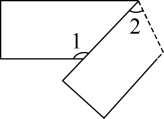 18. 观察等式: , , , 按上述规律,若 , 则 .
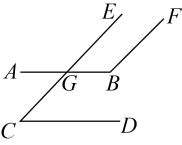
18. 观察等式: , , , 按上述规律,若 , 则 .三、解答题
-
19. 计算: .20. 计算:21. 计算: .22. 利用幂的性质计算: .23. 按要求完成作图并填空:
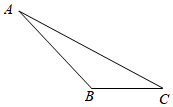 (1)、作∠ABC的平分线,交边AC于点D(尺规作图,保留作图痕迹);(2)、过点A画直线BC的垂线,交直线BC于点E,那么点A到直线BC的距离是线段的长;(3)、在(2)的条件下,如果∠ABC=135°,点B恰好是CE的中点,BC=2cm,那么S△ABC=cm2 .24. 已知:如图,与互补, , 试说明 .
(1)、作∠ABC的平分线,交边AC于点D(尺规作图,保留作图痕迹);(2)、过点A画直线BC的垂线,交直线BC于点E,那么点A到直线BC的距离是线段的长;(3)、在(2)的条件下,如果∠ABC=135°,点B恰好是CE的中点,BC=2cm,那么S△ABC=cm2 .24. 已知:如图,与互补, , 试说明 .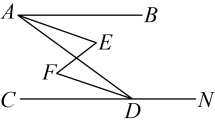
解:因为与互补
所以( )
所以( )
又因为( )
所以 (等式性质)
即
所以( )
所以( )