山西省大同市灵丘县2022-2023学年七年级下学期期中数学质量检测试卷

试卷更新日期：2023-05-25 类型：期中考试

进入出卷网下载

一、单选题

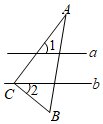
1. 已知实数 $\frac{1}{3}$ ， $\sqrt{3}$ ， $π$ ， $- 2$ ， $0.20020002$ …其中无理数出现的个数为（）

A、2个 B、4个 C、3个 D、5个

查看试题解析
2. 点（﹣4，2）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 点 $M (2 ， 4)$ 向下平移2个单位长度，得到的点的坐标是（）

A、 $(2 ， 2)$ B、 $(0 ， 2)$ C、 $(4 ， 4)$ D、 $(2 ， 6)$

查看试题解析
4. 如图，直线a∥b，直角三角板ABC的直角顶点C在直线b上，若∠1＝55°，则∠2＝（）

A、55° B、45° C、35° D、25°

查看试题解析
5. 下列命题是假命题的是（）

A、同角（等角）的补角相等 B、两直线平行，同位角相等 C、若 $a ∥ b$ ， $a ∥ c$ ，则 $b ∥ c$ D、同一平面内，若 $\vec{a} ⊥ \vec{b}$ ， $a ⊥ c$ ，则 $b ⊥ c$

查看试题解析
6. 如图，下列条件中，不能判定 $A B ∥ C D$ 的是（）

A、 $∠ D + ∠ B A D = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ B = ∠ D C E$

查看试题解析
7. 设n为正整数，且 $n < \sqrt{2022} < n + 1$ ，则n的值为（）

A、42 B、43 C、44 D、45

查看试题解析
8. 如图，为了解决村民饮水困难，需要在河边建立取水点，下面四个点中哪个最方便作为取水点（）

A、A点 B、B点 C、C点 D、D点

查看试题解析
9. 如图， $A B / / C D$ ，点 $E ， F$ 在 $A C$ 边上，已知 $∠ C E D = 70 ° ， ∠ B F C = 130 °$ ，则 $∠ B + ∠ D$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
10. 观察下列等式：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ，
$\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ，
$\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，
…
$\frac{1}{n (n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$
将以上等式相加得到
$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + ⋯ + \frac{1}{n (n + 1)} = 1 - \frac{1}{n + 1}$ ．
用上述方法计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + ⋯ + \frac{1}{99 \times 101}$ 其结果为（）

A、 $\frac{50}{101}$ B、 $\frac{49}{101}$ C、 $\frac{100}{101}$ D、 $\frac{99}{101}$

查看试题解析

二、填空题

11. $\sqrt{16}$ 的算术平方根是

查看试题解析
12. 比较大小： $- \sqrt{5}$ $- 2$ .（填＞、=或＜）

查看试题解析
13. 如图，将一副三角板如图叠放，且EF $∥$ BC，则∠BFD=度．

查看试题解析
14. 点 $M (a + 2, 2 a - 8)$ 是第四象限内一点，若点 $M$ 到两坐标轴的距离相等，则点 $M$ 的坐标为．

查看试题解析
15. 如图，一环湖公路的 $A B$ 段为东西方向，经过四次拐弯后，又变成了东西方向的 $F E$ 段，则 $∠ B + ∠ C + ∠ D + ∠ E$ 的度数是．

查看试题解析

三、解答题

16.

(1)、计算： $- 3^{2} + | \sqrt{2} - 3 | + \sqrt{36}$ ；

(2)、已知 $27 {(x - 1)}^{3} = 64$ ，求x的值．

查看试题解析
17. 已知一个正数的平方根为2a﹣1和﹣a+2，求这个正数．

查看试题解析
18. 如图，两直线 $A B$ 、 $C D$ 相交于点 $O$ ， $O E$ 平分 $∠ B O D$ ，如果 $∠ A O C ： ∠ A O D = 7 ： 11$ ，

(1)、求 $∠ C O E$ ；

(2)、若 $O F ⊥ O E$ ，求 $∠ C O F$ ．

查看试题解析
19. 如图，在平面直角坐标系中，三角形ABC的顶点都在网格格点上，其中B点坐标为（6，4）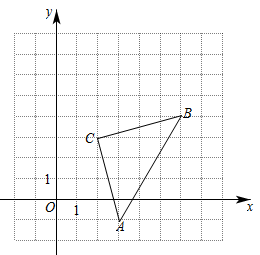

(1)、请写出点A，点C的坐标；

(2)、将△ABC先向左平移1个单位长度，再向上平移3个单位长度，得到△A′B′C′．请画出平移后的三角形，并写出△A′B′C′的三个顶点的坐标；

(3)、求△ABC的面积．

查看试题解析
20. 阅读下列材料，完成相应任务．
台球中的数学
如图1是台球桌面实物图，图2是抽象出的数学图形，已知长方形桌面 $A B C D$ 中， $A D ∥ B C$ ，一个球在桌面上的点 $E$ 处滚向桌边 $A D$ ，碰到 $A D$ 上的点 $F$ 后反弹，再碰到 $B C$ 边上的点 $G$ 后，再次反弹进入底袋点 $D$ ．在球碰到桌边反弹的过程中，击出线与桌边的夹角 $∠ 1$ 等于反弹线与桌边的夹角 $∠ 2$ ，同理 $∠ 3 = ∠ 4$ ．

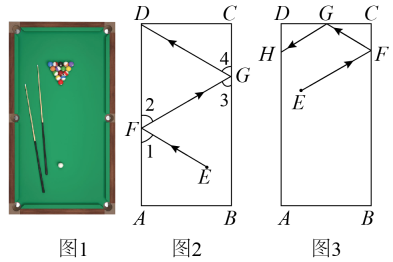(1)、任务一：如图2，求证： $E F ∥ G D$ ；

(2)、任务二：如图3，若球在桌面的点 $E$ 处，经过两次反弹后碰到 $A D$ 边上的点 $H$ 处，若 $∠ C F G + ∠ C G F = 90 °$ ，请你判断 $E F$ 与 $G H$ 的位置关系，并说明理由．

查看试题解析
21. 课上老师提出一个问题：“如图，已知 $A B ∥ C D$ ， $E F ⊥ A B$ 于点 $O$ ， $F G$ 交 $C D$ 于点 $P$ ，当 $∠ 1 = 30 °$ 时，求 $∠ E F G$ 的度数．”
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1，图2，图3所示．

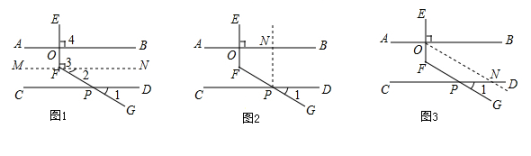(1)、补全甲同学的分析思路．
辅助线：过点 $F$ 作 $M N ∥ C D$ ．
分析思路：
①欲求∠EFG的度数，由图可知只需转化为求  ▲  和  ▲  的度数之和；
②由辅助线作图可知 $∠ 2 = ∠ 1$ ；
③由 $A B ∥ C D$ ， $M N ∥ C D$ 推出  ▲   ，由此可推出 $∠ 3 = ∠ 4$ ；
④由已知 $E F ⊥ A B$ ，可得 $∠ 4 = 90 °$ ，所以可得 $∠ 3$ 的度数，从而可求 $∠ E F G$ 的度数．

(2)、请你根据乙同学所画的辅助线，补全求解过程．
解：过 $P$ 作  ▲   ，交 $A B$ 于点 $N$ ．
$∴$   ▲   $= ∠ E F G$ （两直线平行，同位角相等）．
$∵ E F ⊥ A B$ ，
$∴ ∠ B O F = 90 °$ ，
$∴ ∠ B N P = ∠ B O F = 90 °$ （   ）．
∵ $A B ∥ C D$ ．
$∠ N P D + ∠ B N P = 180 °$ （    ），
$∴ ∠ N P D = 90 °$ ，
$∴ ∠ E F P = ∠ N P G = ∠ N P D + ∠ 1 =$   ▲   ．

(3)、请你根据丙同学所画的辅助线，求 $∠ E F G$ 的度数．

查看试题解析
22. 如图，有一只蚂蚁从点B沿数轴向左爬了2个单位长度到达点A，若点B表示数 $\sqrt{3}$ ，设点A所表示的数为m．

(1)、实数m的值是；

(2)、求 ${(m + 2)}^{2} + | m + 1 |$ 的值．

(3)、在数轴上还有C、D两点分别表示实数c和d，且有 $| 2 c + 4 |$ 与 $\sqrt{d - 4}$ 互为相反数，求 $2 c + 3 d + 8$ 的平方根．

查看试题解析
23. 综合与实践：
问题情境：在综合与实践课上，同学们以“一个含30°角的直角三角尺和两条平行线”为背景开展数学活动．如图1，已知两直线a，b且 $a ∥ b$ 和直角三角形ABC， $∠ B C A = 90 °$ ， $∠ B A C = 30 °$ ， $∠ A B C = 60 °$ ．

(1)、操作发现：在图1中， $∠ 1 = 46 °$ ，求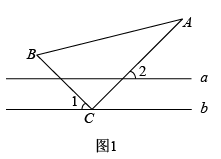 $∠ 2$ 的度数；

(2)、如图2，创新小组的同学把直线a向上平移，并把 $∠ 2$ 的位置改变，发现 $∠ 2 - ∠ 1 = 120 °$ ，说明理由；

(3)、实践探究：缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，AC平分 $∠ B A M$ ，此时发现 $∠ 1$ 与 $∠ 2$ 又存在新的数量关系，请写出你的发现并说明理由．

查看试题解析