江西省萍乡市安源区2022-2023学年七年级下学期期中质量检测数学试卷

试卷更新日期：2023-05-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a^{2} b)}^{3} = a^{2} b^{3}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
2. 甲型流感病毒的直径大约为 $0.0000000081$ 米，用科学记数法表示为（）

A、 $0.81 \times 1 0^{- 9}$ 米 B、 $0.81 \times 1 0^{- 8}$ 米 C、 $8.1 \times 1 0^{- 7}$ 米 D、 $8.1 \times 1 0^{- 9}$ 米

查看试题解析
3. 下列长度的三根木棒首尾相接，能组成三角形的是（）

A、 $3 c m ， 4 c m ， 5 c m$ B、 $7 c m ， 8 c m ， 15 c m$ C、 $6 c m ， 12 c m ， 20 c m$ D、 $5 c m ， 5 c m ， 11 c m$

查看试题解析

4. 小明一家自驾车到离家

500 k m

的某景点旅游，出发前将油箱加满油．下表记录了行驶路程

x (k m)

与油箱余油量

y (L)

之间的部分数据：

行驶路程 $x (k m)$	$0$	$50$	$100$	$150$	$200$	…
油箱余油量 $y (L)$	$45$	$41$	$37$	$33$	$29$	…

下列说法不正确的是（）

A、该车的油箱容量为

45 L

B、该车每行驶

100 k m

耗油

8 L

C、油箱余油量

y (L)

与行驶路程

x (k m)

之间的关系式为

y = 45 - 8 x

D、当小明一家到达景点时，油箱中剩余

5 L

油

查看试题解析

5. 如图，已知 $A B$ // $C D$ ， $∠ A = 40 °$ ， $∠ C = 65 °$ ，则 $∠ P$ 的度数为（）

A、20° B、35° C、30° D、25°

查看试题解析
6. 如图，ΔABC≌ΔDCB，若AC＝7，BE﹦5，则DE的长为（）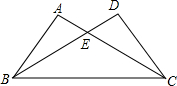

A、2 B、3 C、4 D、5

查看试题解析
7. 如果 $x^{2} + m x + 9$ 是一个完全平方式，则m的值（）

A、6 B、 $\pm 6$ C、3 D、 $\pm 3$

查看试题解析
8. 如果 $m^{2} + m = 3$ ，那么代数式 $m (m - 2) + (m + 2)^{2}$ 的值为（）

A、14 B、10 C、7 D、6

查看试题解析
9. “龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点．用s表示路程，t表示时间，则与故事情节相吻合的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，边长为（m+3）的正方形纸片，剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为3，则另一边长是（）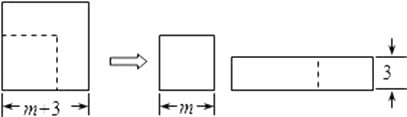

A、m+3 B、m+6 C、2m+3 D、2m+6

查看试题解析

二、填空题

11. 圆的面积 S与半径 r之间有如下关系：S＝πr² ，在这个关系中，常量是，变量是．

查看试题解析
12. 已知△ABC的三个内角满足∠A﹕∠B﹕∠C=1﹕2﹕3，则△ABC是三角形.（填“锐角”“直角”或“钝角”）

查看试题解析
13. 已知 $a + b = 3$ ， $a - b = 1$ ，则 $a^{2} - b^{2} =$ ．

查看试题解析
14. 已知 $(x + a) (x + b) = x^{2} + 5 x + a b$ ， $a + b$ ＝．

查看试题解析
15. 如图，已知直线a∥b，∠1=40°，∠2=60°，则∠3=

查看试题解析
16. 如图，在 $Δ A B C$ 中， $∠ A B C$ ， $∠ A C B$ 的平分线 $B E$ ， $C D$ 相交于点F， $∠ A = 60 °$ ，则 $∠ B F C$ 的度数为.

查看试题解析
17. 如图，把一张长方形纸条ABCD沿EF折叠，若∠1=65°，则∠EGF应为．

查看试题解析
18. 某电视台“中国梦”栏目的一位记者乘汽车赴360km外的农村采访，全程的前一部分为高速公路，后一部分为乡村公路．若汽车在高速公路和乡村公路上分别以某一速度匀速行驶，汽车行驶的路程 $y (k m)$ 与时间 $x (h)$ 之间的关系如图所示，则下列结论正确的是（填序号）．
①汽车在高速公路上的行驶速度为 $90 k m / h$ ；

②乡村公路总长为90km；

③汽车在乡村公路上的行驶速度为 $60 k m / h$ ；

④该记者在出发后5小时到达采访地．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 3^{2} + 202 3^{0} \times (- 3) + {(- \frac{1}{3})}^{- 2}$ ；

(2)、 $202 3^{2} - 2022 \times 2024$

查看试题解析
20. 先化简，再求值： $[(a + b)^{2} - (a - b)^{2} + 6 a^{2} b^{3}] \div (- 2 a b)$ ，其中 $a = - 2$ ， $b = 1$ ．

查看试题解析
21. 如图，已知直线AB、CD被直线EF所截，且∠AGE=46°，∠EHD=134°，请判断AB与CD平行吗？说明理由．

查看试题解析
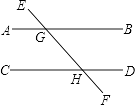22. 在下面的解题过程的横线上填空，并在括号内注明理由．
如图，已知 $∠ A = ∠ F$ ， $∠ C = ∠ D$ ，试说明 $B D ∥ C E$ ．

解：因为 $∠ A = ∠ F$ （已知），

所以 $A C ∥ D F$ （  ）．

所以 $∠ 1 = ∠$   ▲  （  ）．

又因为 $∠ C = ∠ D$ （已知），

所以 $∠ 1 = ∠ C$ （  ）．

所以 $B D ∥ C E$ （  ）．

查看试题解析
23. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ ， $∠ A O E = ∠ C O F = 90 °$ ．

(1)、写出 $∠ D O E$ 的所有余角．

(2)、若 $∠ A O F = 69 °$ ，求 $∠ C O E$ 的度数．

查看试题解析
24. 某市出租车收费标准如下：3千米以内（含3千米）收费11元；超过3千米的部分，每千米收费3元．

(1)、写出应收车费， $y$ （元）与出租车行驶路程 $x$ （千米）之间的关系式（其中 $x ≥ 3$ ）；

(2)、小明从家到体育馆乘出租车行驶6千米应付多少元？

(3)、小明从体育馆到图书馆乘出租车，付车费23元，从体育馆到图书馆出租车行驶了多少千米？

查看试题解析
25. 如图1是一个长为2a，宽为2b的长方形（其中a，b均为正数，且a>b），沿图中虚线用剪刀均匀分成四块相同小长方形，然后按图方式拼成一个大正方形．

(1)、你认为图2中大正方形的边长为；小正方形（阴影部分）的边长为．（用含a，b的代数式表示）

(2)、仔细观察图，请你写出下列三个代数式（a+b）² ，（a-b）² ， ab所表示的图形面积之间的相等关系．

(3)、已知a+b=7，ab=6，求代数式（a-b）²的值．

查看试题解析
26. 基本性质：三角形中线等分三角形的面积．
如图1， $A D$ 是 $△ A B C$ 边 $B C$ 上的中线，则 $S_{△ A B D} = S_{△ A C D} = \frac{1}{2} S_{△ A B C}$ ．

理由：因为 $A D$ 是 $△ A B C$ 边 $B C$ 上的中线，所以 $B D = C D$ ．

又因为 $S_{△ A B D} = \frac{1}{2} B D \times A H$ ， $S_{△ A C D} = \frac{1}{2} C D \times A H$ ，所以 $S_{△ A B D} = S_{△ A C D} = \frac{1}{2} S_{△ A B C}$ ．

所以三角形中线等分三角形的面积．

基本应用：

在如图2至图4中， $△ A B C$ 的面积为a．

(1)、如图2，延长 $△ A B C$ 的边 $B C$ 到点D，使 $C D = B C$ ，连接 $D A$ ．若 $△ A C D$ 的面积为 $S_{1}$ ，则 $S_{1} =$ （用含a的代数式表示）；

(2)、如图3，延长 $△ A B C$ 的边 $B C$ 到点D，延长边 $C A$ 到点E，使 $C D = B C$ ， $A E = C A$ ，连接 $D E$ ．若 $△ D E C$ 的面积为 $S_{2}$ ，则 $S_{2} =$ （用含a的代数式表示）；

(3)、在图3的基础上延长 $A B$ 到点F，使 $B F = A B$ ，连接 $F D$ ， $F E$ ，得到 $△ D E F$ （如图4）．若阴影部分的面积为 $S_{3}$ ，则 $S_{3} =$ （用含a的代数式表示）；

(4)、拓展应用：
如图5，点D是 $△ A B C$ 的边 $B C$ 上任意一点，点E，F分别是线段 $A D$ ， $C E$ 的中点，且 $△ A B C$ 的面积为 $8 a$ ，则 $△ B E F$ 的面积为（用含a的代数式表示），并写出理由．

查看试题解析