江西省抚州市南城县2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 半径是R的圆的周长 , 下列说法正确的是( )A、C, , R是变量,2是常量 B、C是变量,2, , R是常量 C、R是变量,2, , C是常量 D、C,R是变量,是常量3. 下列代数运算正确的是( )A、 B、 C、 D、4. 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的一组对边上,如果∠1=25°,那么∠2的度数是( )
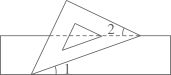 A、30° B、25° C、20° D、15°5. 下列各式中不能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的关系用图象描述大致是( )
A、30° B、25° C、20° D、15°5. 下列各式中不能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的关系用图象描述大致是( )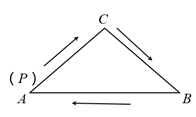 A、
A、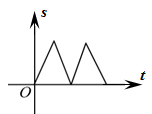 B、
B、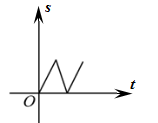 C、
C、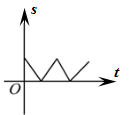 D、
D、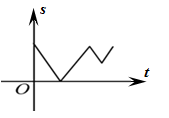
二、填空题
-
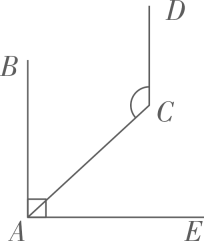
7. 如果一个角等于 , 那么它的补角是 .8. 黄金是自然界中延展性最好的金属.最薄的金箔的厚度为0.000000091m,数据0.000000091用科学记数法表示为 .9. 科学家研究发现声音在空气中传播的速度y(米/秒)与气温有的关系,若今天的气温是 , 则声音的传播速度是米/秒.10. 如图, , , ,则 的度数为 .
 11. 定义一种新运算A※B=A2+AB . 例如(﹣2)※5=(﹣2)2+(﹣2)×5=﹣6.按照这种运算规定,(x+2)※(2﹣x)=20,则x= .12. 如图,在中, , D是线段上一个动点,连接 , 把沿折叠,点C落在同一平面内的点处,当平行于的边时,的大小为 .
11. 定义一种新运算A※B=A2+AB . 例如(﹣2)※5=(﹣2)2+(﹣2)×5=﹣6.按照这种运算规定,(x+2)※(2﹣x)=20,则x= .12. 如图,在中, , D是线段上一个动点,连接 , 把沿折叠,点C落在同一平面内的点处,当平行于的边时,的大小为 .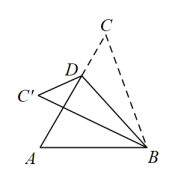
三、解答题
-
13.(1)、用乘法公式计算:(2)、计算:14. 如图,在方格纸中,点C在直线AB外.
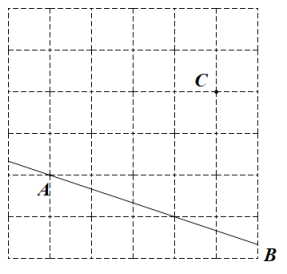 (1)、过点C画AB的垂线CE;(2)、过点C画AB的平行线CH;(3)、通过你的观察,CH与CE的位置关系为 .15. 如图,直线AB与CD相交于点O,于点O,OF平分 . 若:=4:5,求的度数
(1)、过点C画AB的垂线CE;(2)、过点C画AB的平行线CH;(3)、通过你的观察,CH与CE的位置关系为 .15. 如图,直线AB与CD相交于点O,于点O,OF平分 . 若:=4:5,求的度数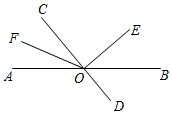 16. 先化简 ,再求值,其中17. 如图,长方形中, , , 点E为边上一动点,连接 , 随着点E的运动,四边形的面积也发生变化.
16. 先化简 ,再求值,其中17. 如图,长方形中, , , 点E为边上一动点,连接 , 随着点E的运动,四边形的面积也发生变化.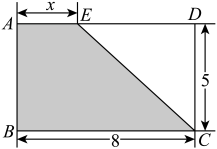 (1)、写出四边形的面积y与的长之间的关系式.(2)、当四边形的面积为25时,求的长.18. 补充完成下面的推理过程.
(1)、写出四边形的面积y与的长之间的关系式.(2)、当四边形的面积为25时,求的长.18. 补充完成下面的推理过程.如图,已知点分别是的边上的点, .
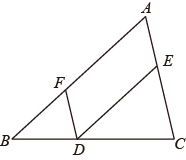
求证: .
证明: , (已知)
▲ ( )
( )
▲ ( )
▲ ▲ ( )
19. 规定两数a,b之间的一种运算,记作:如果 , 那么 . 例如:∵ , ∴
(1)、根据上述规定,填空: , , ;(2)、小明在研究这种运算时发现一个现象: , 小明给出了如下的理由:设 , 则 , 即 ,
∴ , 即 ,
∴ .
请你尝试运用这种方法判断是否成立,若成立,请说明理由.
20. 县建昌大道上安装的护栏平面示意图如图所示,假如每根立柱宽为 , 立柱间距为 . (1)、根据图中信息,将表格补充完整;
(1)、根据图中信息,将表格补充完整;立柱根数
1
2
3
4
5
…
护栏总长度/m
0.2
3.4
9.8
…
(2)、设有x根立柱,护栏总长度为 , 求y与x之间的关系式.(3)、求护栏总长度为时,立柱的根数.21. 上周末,小明坐公交车到象山公园游玩,他从家出发0.8小时后达到图书城,逗留一段时间后继续坐公交车到象山公园,小明离家一段时间后,爸爸驾车沿相同的路线前往象山公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题: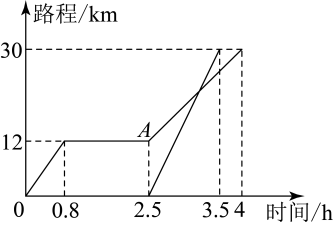 (1)、图中自变量是 , 因变量是;(2)、小明家到象山公园的路程为km,小明在图书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从图书城到象山公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(6)、小明从家到图书城时,他离家路程s与坐车时间t之间的关系式为 .22. 完全平方公式:适当的变形,可以解决很多的数学问题.
(1)、图中自变量是 , 因变量是;(2)、小明家到象山公园的路程为km,小明在图书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从图书城到象山公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(6)、小明从家到图书城时,他离家路程s与坐车时间t之间的关系式为 .22. 完全平方公式:适当的变形,可以解决很多的数学问题.例如:若 , 求的值.
解:设 , 则 , ,
所以
根据上面的解题思路与方法,解决下列问题:
(1)、若 , 求的值;(2)、填空:①若 , 则;
②若 , 则 .
(3)、如图,点C是线段上的一点,以为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分面积.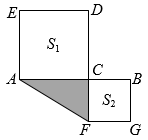 23. 在数学综合与实践课上,老师给出了下列问题:(1)、探究结论:如图1, , , 则 ▲ :
23. 在数学综合与实践课上,老师给出了下列问题:(1)、探究结论:如图1, , , 则 ▲ :如图2, , , 则 ▲

结论:两个角的两边分别平行,则这两个角 ▲ 或 ▲
(2)、应用结论:①若两个角的两边分别平行,其中一个角是另一个角的2倍少60°,则角的度数为 ▲ ;②在图3中,五边形 , 点G、F分别在、上,将∠A沿翻折得到 , , , , , 求的度数.
(3)、拓展应用:在图4中, , , , , 平分 , G点是线段上的一个动点,若中有两个相等的角, , , 直接写出的度数.