江西省九江市修水县2022-2023学年七年级下学期4月期中数学试题

试卷更新日期：2023-05-25 类型：期中考试

进入出卷网下载

一、单选题

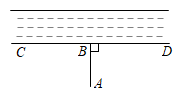
1. 下列运算中，正确的是（）

A、 ${(a^{2})}^{3} = a^{8}$ B、 ${(- 3 a)}^{2} = 6 a^{2}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 $a^{9} \div a^{3} = a^{3}$

查看试题解析
2. 如图，现要从村庄 $A$ 修建一条连接公路 $C D$ 的最短小路，过点 $A$ 作 $A B ⊥ C D$ 于点 $B$ ，沿修建公路，则这样做的理由是（）

A、垂线段最短 B、两点之间，线段最短 C、过一点可以作无数条直线 D、两点确定一条直线

查看试题解析
3. 某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地，全程所用的时间为t(h)，在这个变化过程中，（）

A、s是变量 B、t是常量 C、v是常量 D、s是常量

查看试题解析
4. 下列说法中，正确的是（）

A、相等的角是对顶角 B、两条直线被第三条直线所截，同位角相等 C、在同一平面内，过一点有且仅有一条直线垂直于已知直线 D、一个锐角的补角可能等于该锐角的余角

查看试题解析
5. 如图所示， $A B ∥ C D$ ， $E C ⊥ C D$ ，若 $∠ B E C = 30 °$ ，则 $∠ A B E$ 的度数为（　　）

A、100° B、110° C、120° D、130°

查看试题解析
6. 下列各情境分别可以用哪幅图来近似地刻画？正确的顺序是（）
①紧急刹车的汽车（速度与时间的关系）；

②人的身高变化（身高与年龄的关系）；

③跳跃横杆的跳高运动员（高度与时间的关系）；

④一面冉冉上升的红旗（高度与时间的关系）．

A、abcd B、dabc C、dbca D、cabd

查看试题解析

二、填空题

7. 已知 $∠ A$ 与 $∠ B$ 互余，且 $∠ A = 37 °$ ，则 $∠ B$ 的补角是度.

查看试题解析
8. 某流感球形病毒细胞的直径约为 $0.00000156 m$ ，用科学记数法表示这个数为．

查看试题解析
9. 拖拉机工作时，油箱中的余油量 $Q$ （升）与工作时间 $t$ （时）的关系式为 $Q = 40 - 6 t$ ．从关系式可知这台拖拉机最多可以工作小时．

查看试题解析
10. 若 $3^{m} = 2$ ， $3^{n} = 5$ ，则 $3^{m + 2 n} =$ ．

查看试题解析
11. 某复印店复印收费y（元）与复印面数x面的函数图象如图所示，从图象中可以看出，复印超过100面的部分，每面收费元.

查看试题解析
12. 如图，点 $E$ 在 $A B$ 的延长线上，下列条件：① $∠ 1 = ∠ 3$ ；② $∠ 2 = ∠ 4$ ；③ $∠ D A B = ∠ C B E$ ；④ $∠ D + ∠ B C D = 180 °$ ；⑤ $∠ D C B = ∠ C B E$ ，其中能判断 $A D / / C B$ 的是．（填写正确的序号即可）

查看试题解析

三、解答题

13. 计算：

(1)、 ${(x - 2 y)}^{2} - (x - y) (x + y)$ ．

(2)、 $1001 \times 999 - 99 7^{2}$ ．（利用公式计算）

查看试题解析
14. 如图，利用尺规在 $A D$ 的右侧作 $∠ D C P = ∠ D A B$ （不写作法，只需保留作图痕迹）．

查看试题解析
15. 如图， $A F$ 与 $B D$ 相交于点 $C$ ， $∠ B = ∠ A C B$ ，且 $C D$ 平分 $∠ E C F$ ．试说明： $A B ∥ C E$ ．

查看试题解析
16. 先化简，再求值：
$[(x + 2 y) (x - 2 y) - {(2 x - y)}^{2} - (x^{2} - 5 y^{2})] \div (- 2 x)$ ，其中 $x$ 、 $y$ 满足 $2^{3 x} \div 2^{3 y} = 8$ .

查看试题解析
17. 如图所示，直角梯形ABCD中，O是BC的中点，求 $△ A D O$ 的面积（用含a，b的式子表示）．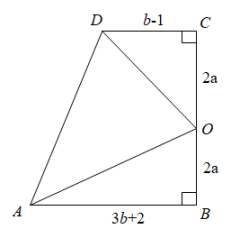

查看试题解析

18. 父亲告诉小明“距离地面越高，温度越低”，并给小明出示了下面的表格．

距离地面的高度 $/ k m$	0	1	2	3	4	5
温度/℃	20	14	8	2	$- 4$	$- 10$

根据上表，父亲还给小明出了下面几个问题，请你和小明一起回答．

(1)、上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

(2)、如果用

h

表示距离地面的高度，用

t

表示温度，那么随着

h

的变化，

t

是怎么变化的？请求出

t

与

h

之间的关系式．

(3)、距离地面

6 k m

的高空的温度是多少？

查看试题解析

19. 如图，在三角形 $A B C$ 中， $C D ⊥ A B$ ，垂足为 $D$ ， $D G$ 与 $A C$ 相交于点 $G$ ，点 $E$ 在 $B C$ 上， $E F ⊥ A B$ ，垂足为 $F$ ， $∠ 1 = ∠ 2$ ．

(1)、试说明 $D G ∥ B C$ 的理由；

(2)、如果 $∠ B = 34 °$ ，且 $∠ A C D = 47 °$ ，求 $∠ 3$ 的度数．

查看试题解析
20. 如图①，长方形ABCD的边长分别为a、b，请认真观察图形，解答下列问题：

(1)、若用四个完全相同的长方形ABCD拼成如图②的正方形，请写出下列三个代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， ab之间的一个等量关系式：．

(2)、根据（1）中的等量关系，解决如下问题：若 $x + y = 7$ ， $x y = 6$ ，求 $x - y$ 的值．

(3)、若将长方形ABCD的各边向外作正方形（如图③），若四个正方形周长之和为32，四个正方形面积之和为20，求出长方形ABCD的面积．

查看试题解析