河北省唐山市路北区2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 如果座位表上“5列2行”记作(5,2),那么(4,3)表示( )A、3列5行 B、5列3行 C、4列3行 D、3列4行2. 下列实数 , , 0, , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个3. 已知实数的一个平方根是2,则它的另一个平方根是( )A、 B、 C、 D、4. 下面四个图形中,与是邻补角的是( )A、
 B、
B、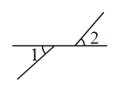 C、
C、 D、
D、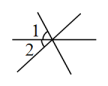 5. 如图,体育课上测量跳远成绩的依据是( )
5. 如图,体育课上测量跳远成绩的依据是( ) A、平行线间的距离相等 B、两点之间,线段最短 C、垂线段最短 D、两点确定一条直线6. 已知正方体的体积为64,则这个正方体的棱长为( )
A、平行线间的距离相等 B、两点之间,线段最短 C、垂线段最短 D、两点确定一条直线6. 已知正方体的体积为64,则这个正方体的棱长为( )
A、4 B、8 C、 D、7. 如图,辽宁省在河北省的( ) A、西偏南方向 B、东偏北方向 C、西偏北方向 D、东偏南方向8. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在下列条件中,不能判定的是( )
A、西偏南方向 B、东偏北方向 C、西偏北方向 D、东偏南方向8. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在下列条件中,不能判定的是( ) A、 B、 C、 D、10. 若与是同一个数的两个不相等的平方根,则这个数是( )A、2 B、 C、4 D、111. 如图,直线与相交于点O,射线在内部,且于点O,若 , 则的度数为( )
A、 B、 C、 D、10. 若与是同一个数的两个不相等的平方根,则这个数是( )A、2 B、 C、4 D、111. 如图,直线与相交于点O,射线在内部,且于点O,若 , 则的度数为( )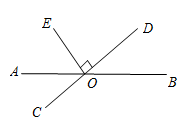 A、125° B、135° C、65° D、55°12. 过和两点的直线一定( )A、垂直于x轴 B、与y轴相交但不平行于x轴 C、平行于x轴 D、与x轴相交但不平行于y轴13. 如图所示,平分 , 平分 , 不能判定的条件是( )
A、125° B、135° C、65° D、55°12. 过和两点的直线一定( )A、垂直于x轴 B、与y轴相交但不平行于x轴 C、平行于x轴 D、与x轴相交但不平行于y轴13. 如图所示,平分 , 平分 , 不能判定的条件是( ) A、 B、 C、 D、14. 如图,将沿着某一方向平移一定的距离得到 , 则下列结论:①;②;③;④中,正确的是( )
A、 B、 C、 D、14. 如图,将沿着某一方向平移一定的距离得到 , 则下列结论:①;②;③;④中,正确的是( ) A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
15. 49的算术平方根是 .16. 如图,点A,B,C在直线l上,PB⊥l , PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是cm.
 17. 若 ,且a,b是两个连续的整数,则a+b的值为18. 如图,在平面直角坐标系中,点在y轴正半轴上,占在x轴负半轴上,且 , 点M坐标为 , N点为线段上一动点,P为线段上的一动点.
17. 若 ,且a,b是两个连续的整数,则a+b的值为18. 如图,在平面直角坐标系中,点在y轴正半轴上,占在x轴负半轴上,且 , 点M坐标为 , N点为线段上一动点,P为线段上的一动点. (1)、的面积为;(2)、的最小值为 .
(1)、的面积为;(2)、的最小值为 .三、解答题
-
19. 计算:(1)、;(2)、;20. 如图是一个数值转换程序.
 (1)、当整数x的值为16时,求输出y的值;(2)、在输入整数x值后,始终输不出y值的情况?如果存在,请直接写出所有满足要求的x的值;如果不存在,请说明理由;(3)、一个两位数x,恰好经过两次取算术平方根才能输出无理数,直接写出这样的x有多少个.21. 如图,网格线的交点叫格点,格点P是的边上的一点(请用无刻度的直尺借助网格的格点画图,保留画图痕迹).
(1)、当整数x的值为16时,求输出y的值;(2)、在输入整数x值后,始终输不出y值的情况?如果存在,请直接写出所有满足要求的x的值;如果不存在,请说明理由;(3)、一个两位数x,恰好经过两次取算术平方根才能输出无理数,直接写出这样的x有多少个.21. 如图,网格线的交点叫格点,格点P是的边上的一点(请用无刻度的直尺借助网格的格点画图,保留画图痕迹).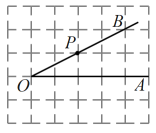 (1)、过点P画的垂线,交于点E;过点P画的垂线,垂足为F;(2)、线段这三条线段大小关系是(用“”号连接),理由是 .22. 已知: , .(1)、若x,y分别为点P的横、纵坐标,求点的坐标;(2)、求的算术平方根.23. 如图,平分 , , , .
(1)、过点P画的垂线,交于点E;过点P画的垂线,垂足为F;(2)、线段这三条线段大小关系是(用“”号连接),理由是 .22. 已知: , .(1)、若x,y分别为点P的横、纵坐标,求点的坐标;(2)、求的算术平方根.23. 如图,平分 , , , . (1)、求 , 的度数;(2)、证明: .24. 如图,△ABC三个顶点的坐标分别是 , , .
(1)、求 , 的度数;(2)、证明: .24. 如图,△ABC三个顶点的坐标分别是 , , .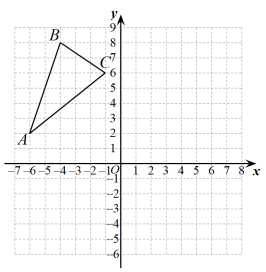 (1)、画出向右平移7个单位向下平移6个单位后的图形 , 并写出 , 两个顶点的坐标.(2)、求的面积.(3)、 与x轴交点的横坐标.25. 已知点是直角坐标系内一点.(1)、若点A在y轴上,求出点A的坐标;(2)、经过点 , 的直线,与x轴平行,求出点A的坐标;(3)、点A到两坐标轴的距离相等,点A的坐标.26. 已知:如图,直线与分别相交于点E,F.
(1)、画出向右平移7个单位向下平移6个单位后的图形 , 并写出 , 两个顶点的坐标.(2)、求的面积.(3)、 与x轴交点的横坐标.25. 已知点是直角坐标系内一点.(1)、若点A在y轴上,求出点A的坐标;(2)、经过点 , 的直线,与x轴平行,求出点A的坐标;(3)、点A到两坐标轴的距离相等,点A的坐标.26. 已知:如图,直线与分别相交于点E,F. (1)、如图1,若 , , 和的位置关系为;(2)、在(1)的情兄下,若点P是平面内的一个动点,连接 , 探索三个角之间的关系;
(1)、如图1,若 , , 和的位置关系为;(2)、在(1)的情兄下,若点P是平面内的一个动点,连接 , 探索三个角之间的关系;①当点P在图2的位置时,可得;
请阅读下面的解答过程,并填空(理由或数学式):
解:如图2、过点P作 ,
则( ).
∵(已知),(作图),
∴( ).
∴ .
∴( ).
即;
②当点P在图3的位置时,求三个角之间有何数量关系;
③当点P在图4的位置时,请三个角之间的关系.