广东省深圳市育才教育集团2022-2023学年七年级下学期期中考试数学试卷
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 淋巴细胞是机体免疫应答功能的重要细胞成分,是对抗外界感染和监控体内细胞变异的一线“士兵”,最小的淋巴细胞直径仅 . 则下列用科学记数法表示正确的是( )A、 B、 C、 D、2. 计算:的结果是( )A、 B、 C、 D、3. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、4cm,4cm,10cm C、3cm,1cm,3cm D、3cm,4cm,9cm4. 如图,已知直线和相交于点 , 是直角,平分 , , 则的度数为( )
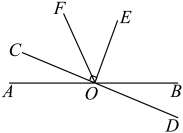 A、 B、 C、 D、72°5. 下列说法正确的是( )
A、 B、 C、 D、72°5. 下列说法正确的是( )①若线段与没有交点,则 .
②平行于同一条直线的两条直线互相平行.
③过一点有且只有一条直线与已知直线垂直.
④过直线外一点作已知直线的垂线段,垂线段的长度叫做这个点到这条直线的距离.
A、①②③④ B、①②④ C、②③ D、②④6. 如图, , , , 图中全等的三角形的对数是( )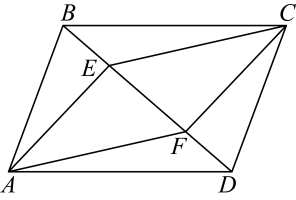 A、4 B、5 C、6 D、77. 若是完全平方式,则的值是( )A、4 B、8 C、4或-4 D、8或-88. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )
A、4 B、5 C、6 D、77. 若是完全平方式,则的值是( )A、4 B、8 C、4或-4 D、8或-88. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )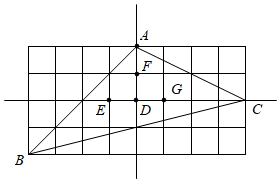 A、点 B、点 C、点 D、点9. 课本中给出了用直尺和圆规作的平分线的方法.
A、点 B、点 C、点 D、点9. 课本中给出了用直尺和圆规作的平分线的方法.作法
图形
①以点O为圆心,任意长为半径作弧,分别交射线、于点C、D.②分别以点C、D为圆心,大于的长为半径作弧,两弧在的内部交于点M.
③作射线 .
就是的平分线.
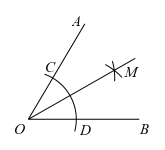
该作图依据是( )
A、 B、 C、 D、10. 如图,在中, , , , 点为的中点,如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.若在某一时刻能使与全等.则点的运动速度为( )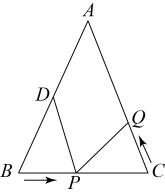 A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题
-
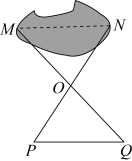
11. 如图,小强利用全等三角形的知识测量池塘两段的距离.如果 , 则池塘两段的距离为 .
 12. 小佳计划用一根长为的铁丝围成一个长方形,那么这个长方形的长与宽之间的关系式为 .13. 如果一个角的补角是122°,那么这个角的余角是 .14. 已知 , , 那么 .15. 定义:如果一个三角形的两个内角与满足 , 那么我们称这样的三角形为“准直角三角形”.如图,将三角形纸片沿着折叠,使得点落在边上的点处,已知 . 设 , 当和同时成为“准直角三角形”时.的值为 .
12. 小佳计划用一根长为的铁丝围成一个长方形,那么这个长方形的长与宽之间的关系式为 .13. 如果一个角的补角是122°,那么这个角的余角是 .14. 已知 , , 那么 .15. 定义:如果一个三角形的两个内角与满足 , 那么我们称这样的三角形为“准直角三角形”.如图,将三角形纸片沿着折叠,使得点落在边上的点处,已知 . 设 , 当和同时成为“准直角三角形”时.的值为 .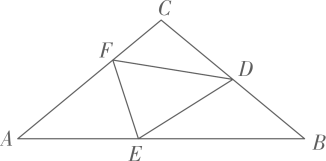
三、解答题
-
16. 计算:(1)、(2)、17. 先化简,再求值: , 其中 ,18. 完成下面的解题过程:
如图,AD//BC,点F是AD上一点,CF与BA的延长线相交于点E,且∠1=∠2,∠3=∠4.CD与BE平行吗?为什么?
解:CD//BE,理由如下:
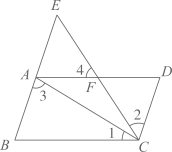
∵AD//BC(已知),
∴∠4= ▲ ( )
∵∠3=∠4(已知),
∴∠3= ▲ ( )
∵∠1=∠2(已知),
∴∠1+∠ACE=∠2+∠ACE ( )
即∠BCE= ▲
∴∠3= ▲
∴CD//BE( )
19. 上周末,小明坐公交车到象山公园游玩,他从家出发0.8小时后达到图书城,逗留一段时间后继续坐公交车到象山公园,小明离家一段时间后,爸爸驾车沿相同的路线前往象山公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题: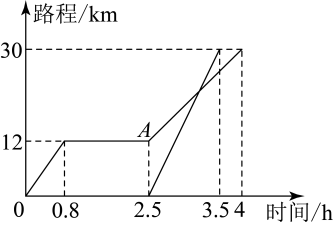 (1)、图中自变量是 , 因变量是;(2)、小明家到象山公园的路程为km,小明在图书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从图书城到象山公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(6)、小明从家到图书城时,他离家路程s与坐车时间t之间的关系式为 .20. 如图,已知△ABC中,∠B=60°,AD是BC边上的高,AE是∠BAC的平分线,且∠1=10°,求∠C的度数
(1)、图中自变量是 , 因变量是;(2)、小明家到象山公园的路程为km,小明在图书城逗留的时间为h;(3)、小明出发小时后爸爸驾车出发;(4)、图中A点表示;(5)、小明从图书城到象山公园的平均速度为km/h,小明爸爸驾车的平均速度为km/h;(6)、小明从家到图书城时,他离家路程s与坐车时间t之间的关系式为 .20. 如图,已知△ABC中,∠B=60°,AD是BC边上的高,AE是∠BAC的平分线,且∠1=10°,求∠C的度数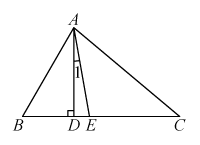 21. 在数学中,有许多关系都是在不经意间被发现的,请认真观察图形,解答下列问题:
21. 在数学中,有许多关系都是在不经意间被发现的,请认真观察图形,解答下列问题: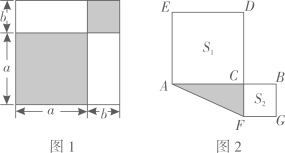 (1)、如图1,用两种不同的方法表示阴影图形的面积,得到一个等量关系: .(2)、如图1中, , 满足 , , 求的值.(3)、如图2,点在线段上,以 , 为边向两边作正方形, , 两正方形的面积分别为 , , 且 , 求图中阴影部分面积.22. 在中, , 点是射线上一动点(不与点 , 重合),以为一边在的右侧作 , 使 , , 连接 .
(1)、如图1,用两种不同的方法表示阴影图形的面积,得到一个等量关系: .(2)、如图1中, , 满足 , , 求的值.(3)、如图2,点在线段上,以 , 为边向两边作正方形, , 两正方形的面积分别为 , , 且 , 求图中阴影部分面积.22. 在中, , 点是射线上一动点(不与点 , 重合),以为一边在的右侧作 , 使 , , 连接 . (1)、如图1,当点在线段上时,与有何数量关系,请说明理由;(2)、在(1)的条件下,当时,那么度;(3)、设 , .
(1)、如图1,当点在线段上时,与有何数量关系,请说明理由;(2)、在(1)的条件下,当时,那么度;(3)、设 , .①如图2,当点在线段上,时,请探究与之间的数量关系,并证明你的结论;
②如图3,当点在线段的延长线上,时,请将图3补充完整并直接写出此时与之间的数量关系.