广东省汕尾市2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-05-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、0 B、－1 C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 在平面直角坐标中，点 $M (- 2 ， 3)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. $\sqrt{7}$ 的相反数是（）

A、 $- \sqrt{7}$ B、 $\sqrt{- 7}$ C、 $\frac{1}{\sqrt{7}}$ D、 $\sqrt{7}$

查看试题解析
4. 在下列图形中，不能通过其中一个四边形平移得到的是（）

A、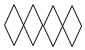 B、 C、 D、

查看试题解析
5. 估计 $\sqrt{6}$ 的值是在（）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
6. 在平面直角坐标系中，将点 $P (1 ， 4)$ 向下平移3个单位长度，再向右平移2个单位长度得到点Q，则点Q的坐标是（）

A、 $(3 ， 1)$ B、 $(4 ， 2)$ C、 $(- 1 ， 1)$ D、 $(4 ， - 1)$

查看试题解析
7. 如图， $a ∥ b$ ， $∠ 1 = 55 °$ ，求 $∠ 2$ 的度数．下面是小云同学的解题过程：

解：如图，

∵ $∠ 1 = 55 °$ ，

∴ $∠ 3 = 125 °$ ．

∵ $a ∥ b$ ，

∴ $∠ 2 = ∠ 3 = 125 °$ （填依据）．

则下列关于依据描述正确的是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
8. 小林在学习平面直角坐标系后，将如图所示的动物园的部分地图与平面直角坐标系联系起来，若“大象馆”的坐标为 $(- 1 ， 1)$ ， “熊猫馆”的坐标为 $(- 2 ， 3)$ ，则“企鹅馆”的坐标为（）

A、 $(2 ， 1)$ B、 $(1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(1 ， - 2)$

查看试题解析
9. 下列图形中，能说明“相等的角是对顶角”为假命题的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，若 $A B ∥ C D$ ，用含有∠1，∠2，∠3的式子表示∠α，则∠α应为（）

A、 $∠ 1 + ∠ 2 + ∠ 3$ B、 $∠ 2 + ∠ 3 - ∠ 1$ C、 $180 ° + ∠ 1 + ∠ 2 - ∠ 3$ D、 $180 ° + ∠ 2 - ∠ 1 - ∠ 3$

查看试题解析

二、填空题

11. $\sqrt{9}$ 的平方根是

查看试题解析
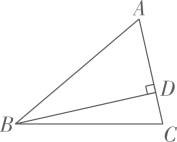
12. 春节假期期间，小刚去电影院观看《流浪地球2》，若将小刚的座位“7排11号”简记为（7，11），则同一场次“8排10号”的座位简记为．

查看试题解析
13. 如图，点C到BD的距离是一条线段的长，这条线段是．

查看试题解析
14. 如图，将三角形 $A B C$ 沿 $B C$ 向右平移得到三角形 $D E F$ ，连接 $A D$ ，若三角形 $A B C$ 的周长是 $8 c m$ ，四边形 $A B F D$ 的周长是 $12 c m$ ，则平移的距离是cm．

查看试题解析
15. 我们知道 $\sqrt{2}$ 是无理数，所以 $\sqrt{2}$ 的小数部分不能全部写出来，但我们可以用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分．已知 $5 + \sqrt{11}$ 的小数部分是a， $5 - \sqrt{11}$ 的小数部分是b，则 ${(a + b)}^{2023}$ 的值为．

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt[3]{- 64} - \sqrt[3]{27} + | - \sqrt{3} |$ ；

(2)、 $| \sqrt{3} - 2 | + \sqrt{{(- 4)}^{2}}$ ．

查看试题解析
17. 在平面直角坐标系中，已知点 $A (2 - a ， 2 a + 4)$ ．

(1)、若点A在x轴上，求点A的坐标．

(2)、若点B的坐标为 $(1 ， 4)$ ，且 $A B ∥ y$ 轴，求点A的坐标．

查看试题解析
18. 如图，直线 $A B$ ， $C D$ 相交于点O， $O E ⊥ A B$ ，若 $O A$ 平分 $∠ D O F$ 且 $∠ D O E = 50 °$ ，求 $∠ C O F$ 的度数．

查看试题解析
19. 已知 $3 a - 2$ 的平方根是 $\pm 2$ ， $a - 2 b - 4$ 的立方根是 $- 2$ ．

(1)、求a，b的值．

(2)、求 $2 a + b$ 的算术平方根．

查看试题解析
20. 如图，把两个面积均为 $18 c m^{2}$ 的小正方形分别沿对角线裁剪后拼成一个大的正方形．

(1)、求大正方形的边长．

(2)、若沿此大正方形边的方向裁剪出一个长方形，能否使裁剪出的长方形纸片的长宽之比为 $3 ： 1$ ，且面积为 $24 c m^{2}$ ．若能，试求剪出的长方形纸片的长宽；若不能，试说明理由．

查看试题解析
21. 如图，在平面直角坐标系中，已知点 $A (- 2 ， 2)$ ， $B (- 3 ， 6)$ ， $C (- 5 ， 3)$ ， $D (m ， n)$ 是三角形 $A B C$ 的边 $A B$ 上任意一点，三角形 $A B C$ 经过平移后得到三角形 $A_{1} B_{1} C_{1}$ ，点D的对应点为点 $D_{1} (m + 5 ， n - 4)$ ．

(1)、直接写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

(2)、在图中画出三角形 $A_{1} B_{1} C_{1}$ ．

(3)、求出三角形 $A B C$ 的面积．

查看试题解析
22. 如图，线段 $A B$ 交线段 $C D$ ， $E F$ 于点H，G，已知 $∠ B H D = ∠ B D H$ ， $∠ C H G = ∠ C$ ，

(1)、求证： $A C ∥ B E$ ．

(2)、若 $∠ B H D + ∠ H G F = 180 °$ ，求证： $∠ C + ∠ C F G = 180 °$ ．

(3)、在（2）的条件下，若 $∠ C F G + 30 ° = 2 ∠ B D H$ ，求 $∠ C$ 的度数．

查看试题解析
23. 如图，在平面直角坐标系中，已知点 $A (a ， 0)$ ， $B (0 ， b)$ ， $C (c ， 0)$ ，且a，b，c满足关系式 $| a - 4 | + {(b - 2)}^{2} + | c + 2 | = 0$ ，点 $P (m ， n)$ 在第一象限．

(1)、求a，b，c的值．

(2)、连接 $B C$ ，当 $S_{三角形 A B C} = \frac{3}{2} S_{三角形 A B P}$ （S代表面积）时，求 $S_{三角形 A B P}$ 的值．

(3)、当 $m = 3$ ， $n > 2$ 时，三角形 $A B P$ 的面积为7，求n的值．

查看试题解析