北京市大兴区2022-2023学年七年级下学期期中考试数学试卷
试卷更新日期:2023-05-25 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、81 B、 C、 D、32. 在平面直角坐标系中,下列各点在第二象限的是( )A、 B、 C、 D、3. 如图所示,线段经过平移后得到的线段是( )
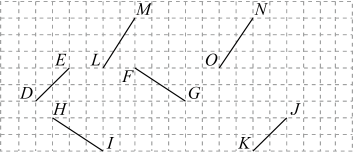 A、 B、 C、 D、4. 如图, , , 则点B到直线的距离是线段( )
A、 B、 C、 D、4. 如图, , , 则点B到直线的距离是线段( ) A、的长 B、的长 C、的长 D、的长5. 下列各数中没有平方根的是( )A、(-3)2 B、0 C、 D、-636. 如图,在数轴上表示实数 的点可能( ).
A、的长 B、的长 C、的长 D、的长5. 下列各数中没有平方根的是( )A、(-3)2 B、0 C、 D、-636. 如图,在数轴上表示实数 的点可能( ). A、点P B、点Q C、点M D、点N7. 如图,下列结论正确的是( )
A、点P B、点Q C、点M D、点N7. 如图,下列结论正确的是( ) A、与是对顶角 B、与是同位角 C、与是同旁内角 D、与是内错角8. 如图,相交于点O, , , 有如下四个结论:
A、与是对顶角 B、与是同位角 C、与是同旁内角 D、与是内错角8. 如图,相交于点O, , , 有如下四个结论:①;②;③;④ .
上面结论中,所有正确结论的序号是( )
 A、①② B、①②④ C、①②③ D、①②③④
A、①② B、①②④ C、①②③ D、①②③④二、填空题
-
9. 写出一个大于的无理数 .10. 的值是 .11. 将点P(﹣2,﹣3)向右平移5个单位长度得点P′.则点P′的坐标为 .12. 如图,点C在射线上,只需添加一个条件即可证明 , 这个条件可以是(写出一个即可).
 13. 如图,直线相交于点O, , O为垂足,如果 , 则 .
13. 如图,直线相交于点O, , O为垂足,如果 , 则 . 14. 命题“对顶角相等”的题设是 , 结论是 .15. 在平面直角坐标系中,点到x轴的距离是4,则A点的坐标是 .16. 在平面直角坐标系中, , , 若 , 且 , 则点C的坐标为 .
14. 命题“对顶角相等”的题设是 , 结论是 .15. 在平面直角坐标系中,点到x轴的距离是4,则A点的坐标是 .16. 在平面直角坐标系中, , , 若 , 且 , 则点C的坐标为 .三、解答题
-
17. 计算: .18. 计算:( , , 结果保留2位小数).19. 已知 , 求x的值.20. 如图,建立平面直角坐标系,使点B的坐标为 , 点C的坐标为 , 并写出点A的坐标.
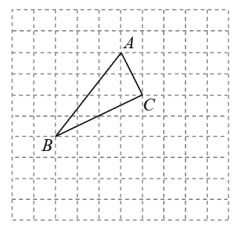 21. 如图,在平面直角坐标系中,三角形三个顶点的坐标分别是 , , . 将三角形平移,使点C与点O重合,得到三角形 , 其中点A,B的对应点分别为 , .
21. 如图,在平面直角坐标系中,三角形三个顶点的坐标分别是 , , . 将三角形平移,使点C与点O重合,得到三角形 , 其中点A,B的对应点分别为 , . (1)、画出三角形;(2)、写出点 , 的坐标.22. 看图填写.
(1)、画出三角形;(2)、写出点 , 的坐标.22. 看图填写.已知:如图, , , . 求证:平分 .

证明:∵ , ,
∴ , . ( )(填推理依据)
∴ .
∴ . ( )(填推理依据)
∴ . ( )(填推理依据)
. ( )(填推理依据)
又∵ , ∴ .
∴平分 . ( )(填推理依据)
23. 已知 , 其中x,y是有理数.求证: , .24. 如图,平分 , , 求证: . 25. 已知:如图, , 过AC上一点D,作交BC于点F.求证: .
25. 已知:如图, , 过AC上一点D,作交BC于点F.求证: .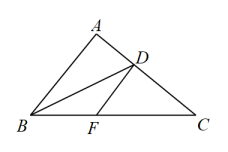 26. 如图,已知线段 , 分别以点A,B为端点作射线 , C,D,E三点分别在上,过点C的直线与线段分别交于点F,H,已知 , .
26. 如图,已知线段 , 分别以点A,B为端点作射线 , C,D,E三点分别在上,过点C的直线与线段分别交于点F,H,已知 , . (1)、判断与的位置关系并加以证明;(2)、若 , , 求的度数.27. 在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.已知点 , , , 其中m为正整数,且A,B,C三点不在同一直线上,分别连接 , 设这三条线段围成的区域内部(不包括线段上的点)的整点个数为n.
(1)、判断与的位置关系并加以证明;(2)、若 , , 求的度数.27. 在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.已知点 , , , 其中m为正整数,且A,B,C三点不在同一直线上,分别连接 , 设这三条线段围成的区域内部(不包括线段上的点)的整点个数为n. (1)、当时,直接写出整点个数n,并写出这些整点的坐标;(2)、若 , 则m的值为;(3)、若 , 则m的值为 .28. 在同一平面内,如果线段外一点到这条线段所在的直线的距离是2,我们称这个点为这条线段的“标准距离点”.例如,图1中点P为线段外一点,点P到线段所在的直线的距离是2,则称点P是线段的“标准距离点”.如图2,平面直角坐标系中,点 , 点在第二象限.
(1)、当时,直接写出整点个数n,并写出这些整点的坐标;(2)、若 , 则m的值为;(3)、若 , 则m的值为 .28. 在同一平面内,如果线段外一点到这条线段所在的直线的距离是2,我们称这个点为这条线段的“标准距离点”.例如,图1中点P为线段外一点,点P到线段所在的直线的距离是2,则称点P是线段的“标准距离点”.如图2,平面直角坐标系中,点 , 点在第二象限. (1)、在点 , , 中,线段的“标准距离点”是(只填字母);(2)、若点B是线段的“标准距离点”.
(1)、在点 , , 中,线段的“标准距离点”是(只填字母);(2)、若点B是线段的“标准距离点”.①a的值为 ▲ ;
②点C是x轴上一点(点C不与点A重合),三角形的面积等于三角形的面积,直接写出点C的坐标;
③已知点是线段的“标准距离点”,其中 , n是正数,连接交线段于点E,点F在x轴上,如果三角形的面积等于三角形的面积,求点F的坐标(用含m的式子表示).