广东省深圳市31校2022-2023学年中考联考二模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最大的是( )A、 B、0 C、3 D、2. 2023年1月2日,第十八届中国(深圳)国际文化产业博览交易会落下帷幕,深圳文化产业增加值突破2600亿元,深圳以其独具特色的工业底座和科技内涵为城市塑造了精神坐标,沉淀着独有的文化记忆.2600亿用科学记数法表示为( )A、 B、 C、 D、3. 我国的生活垃圾一般可分为四大类:厨余垃圾、可回收垃圾、有害垃圾和其他垃圾,图标如下,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算错误的是( )A、 B、 C、 D、5. 酸雨是指雨、雪等在形成和降落过程中,吸收并溶解了空气中的二氧化硫、氮氧化合物等物质,形成了值低于5.6的酸性降水.某学校化学课外活动小组的同学在降雨后用计对雨水的值进行了测试,测试结果如下:
4. 下列运算错误的是( )A、 B、 C、 D、5. 酸雨是指雨、雪等在形成和降落过程中,吸收并溶解了空气中的二氧化硫、氮氧化合物等物质,形成了值低于5.6的酸性降水.某学校化学课外活动小组的同学在降雨后用计对雨水的值进行了测试,测试结果如下:出现的频数
5
8
7
13
7
PH
4.8
4.9
5.0
5.2
5.3
下列说法错误的是( )
A、众数是5.2 B、中位数是5.1 C、极差是0.5 D、平均数是5.16. 学了圆后,小亮突发奇想,想到用这种方法测量三角形的角度:将三角形纸片如图1放置,使得顶点C在量角器的半圆上,纸片另外两边分别与量角器交于A,B两点.点A,B的度数是 , , 这样小明就能得到的度数.请你帮忙算算的度数是( ) A、 B、 C、 D、7. 下列命题中,是真命题的是( )A、如果 , 那么; B、对角线垂直的四边形是菱形; C、关于的一元二次方程没有实数根; D、经过直径的一端且垂直于这条直径的直线是圆的切线.8. 《张丘建算经》中有这样一首古诗:甲乙隔溪牧羊,二人互相商量;甲得乙羊九只,多乙一倍正当;乙说得甲九只,两人羊数一样;问甲乙各几羊,让你算个半晌,如果设甲有羊x只,乙有羊y只,那么可列方程组( )A、 B、 C、 D、9. 如图,函数与的图象如图所示,以下结论正确的是( )
A、 B、 C、 D、7. 下列命题中,是真命题的是( )A、如果 , 那么; B、对角线垂直的四边形是菱形; C、关于的一元二次方程没有实数根; D、经过直径的一端且垂直于这条直径的直线是圆的切线.8. 《张丘建算经》中有这样一首古诗:甲乙隔溪牧羊,二人互相商量;甲得乙羊九只,多乙一倍正当;乙说得甲九只,两人羊数一样;问甲乙各几羊,让你算个半晌,如果设甲有羊x只,乙有羊y只,那么可列方程组( )A、 B、 C、 D、9. 如图,函数与的图象如图所示,以下结论正确的是( )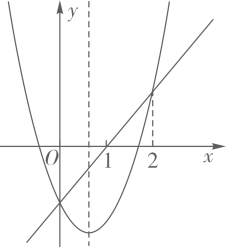 A、 B、 C、 D、当时,10. 如图是物体在焦距为(即)的凸透镜下成倒立放大实像的光路示意图.从点发出的平行于的光束折射后经过右焦点 , 而经过光心点的光束不改变方向,最后点发出的光汇聚于点 , 点发出的光汇聚于点 , 从而得到最清晰的实像.若物距 , 则像距为( )cm.
A、 B、 C、 D、当时,10. 如图是物体在焦距为(即)的凸透镜下成倒立放大实像的光路示意图.从点发出的平行于的光束折射后经过右焦点 , 而经过光心点的光束不改变方向,最后点发出的光汇聚于点 , 点发出的光汇聚于点 , 从而得到最清晰的实像.若物距 , 则像距为( )cm. A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
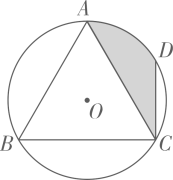
11. 因式分解: .12. 小明向如图所示的圆形区域内投掷飞镖.已知是等边三角形,D点是弧AC的中点,则飞镖落在阴影部分的概率为.
 13. 定义新运算“”,规定: , 若关于的不等式组的解集为 , 则的取值范围是.14. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在O点正下方的P处有一个钉子.已知在O点测得起始位置A的俯角是 , B点的俯角是 , B点测得钉子P的仰角是 , 且长为4,则摆绳长为 .
13. 定义新运算“”,规定: , 若关于的不等式组的解集为 , 则的取值范围是.14. 如图,一同学进行单摆运动实验,从A点出发,在右侧达到最高点B.实验过程中在O点正下方的P处有一个钉子.已知在O点测得起始位置A的俯角是 , B点的俯角是 , B点测得钉子P的仰角是 , 且长为4,则摆绳长为 . 15. 如图,等腰直角中, , 顶点M,P在正方形的边及边的延长线上动点.交于点F,连接并延长,交于N,交于点E.以下结论:①②③④若 , 则 , 其中正确的是 . (填写正确的序号)
15. 如图,等腰直角中, , 顶点M,P在正方形的边及边的延长线上动点.交于点F,连接并延长,交于N,交于点E.以下结论:①②③④若 , 则 , 其中正确的是 . (填写正确的序号)
三、解答题
-
16. 计算:17. 对于“已知 , 求的最大值”这个问题,小明是这样求解的:
∵ , ∴ , ∴
∴ , 所以的最大值为.
请你按照这种方法计算:当时,的最小值.
18. 深圳市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“A电工、B园艺、C厨艺、D木工、E编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图:
根据以上信息,回答下列问题:
(1)、本次调查的样本容量为;统计图中的 , ;(2)、通过计算补全条形统计图;(3)、E类所对应扇形的圆心角的大小为 ;(4)、该校共有3000名学生,请你估计全校喜爱“厨艺”的学生人数.19. 如图,已知中 , , E是的中点,连接并延长,与的延长线交于点F,与交于点G,连接 .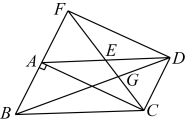 (1)、求证:四边形是矩形.(2)、若的面积是18,求的长.20. 已知一次函数()和反比例函数的图象如图所示.
(1)、求证:四边形是矩形.(2)、若的面积是18,求的长.20. 已知一次函数()和反比例函数的图象如图所示. (1)、一次函数必定经过点 . (写点的坐标)(2)、当时,一次函数与反比例函数图象交于点A,B,与x,y轴分别交于点C,D,连接并延长,交反比例另一支于点E,求出此时A,B两点的坐标及的面积.(3)、直线绕点C旋转,直接写出当直线与反比例图象无交点时m的取值范围.21. 按要求解答(1)、某市计划修建一条隧道,已知隧道全长2400米,一工程队在修了1400米后,加快了工作进度,每天比原计划多修5米,结果提前10天完成,求原计划每天修多长?(2)、隧道建成后的截面图如图所示,它可以抽象成如图所示的抛物线.已知两个车道宽度米,人行道地基AC,BD宽均为2米,拱高米.建立如图所示的直角坐标系.
(1)、一次函数必定经过点 . (写点的坐标)(2)、当时,一次函数与反比例函数图象交于点A,B,与x,y轴分别交于点C,D,连接并延长,交反比例另一支于点E,求出此时A,B两点的坐标及的面积.(3)、直线绕点C旋转,直接写出当直线与反比例图象无交点时m的取值范围.21. 按要求解答(1)、某市计划修建一条隧道,已知隧道全长2400米,一工程队在修了1400米后,加快了工作进度,每天比原计划多修5米,结果提前10天完成,求原计划每天修多长?(2)、隧道建成后的截面图如图所示,它可以抽象成如图所示的抛物线.已知两个车道宽度米,人行道地基AC,BD宽均为2米,拱高米.建立如图所示的直角坐标系.①此抛物线的函数表达式为 ▲ . (函数表达式用一般式表示)
②按规定,车顶部与隧道顶部在竖直方向上的高度差至少0.5米,则此隧道限高 ▲ 米.
③已知人行道台阶高均为0.3米,按照国家标准,人行道宽度不得低于1.25米,该隧道的人行道宽度设计是否达标?说明理由.
+

 22. “同弧或等弧所对的圆周角相等”,利用这个推论可以解决很多数学问题.
22. “同弧或等弧所对的圆周角相等”,利用这个推论可以解决很多数学问题.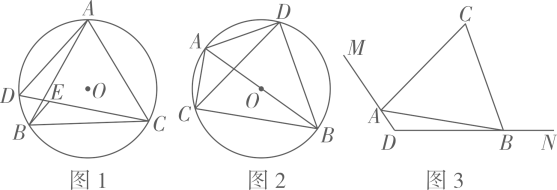 (1)、【知识理解】如图1,圆的内接四边形中, , ,
(1)、【知识理解】如图1,圆的内接四边形中, , ,①;(填“”,“”,“”)
②将点绕点顺时针旋转得到点 , 则线段的数量关系为 .
(2)、【知识应用】如图2,是圆的直径, , 猜想的数量关系,并证明;(3)、【知识拓展】如图3,已知 , 分别是射线上的两个动点,以为边往外构造等边 , 点在内部,若 , 直接写出四边形面积的取值范围.