云南省玉溪市2023年中考一模数学试卷

试卷更新日期：2023-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 在0，－3， $\sqrt{2}$ ， 1四个数中，最大的数是（）

A、0 B、－3 C、 $\sqrt{2}$ D、1

查看试题解析
2. 襄阳市正在创建全国文明城市，某社区从今年6月1日起实施垃扱分类回收．下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志，其中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $3 \sqrt{2} - \sqrt{2} = 3$ B、 ${(a - 1)}^{2} = a^{2} - 1$ C、 ${(a^{3})}^{2} = a^{5}$ D、 $4 a^{2} \cdot a = 4 a^{3}$

查看试题解析
4. 如图， $A B ∥ C D$ ，直线 $E F$ 分别交 $A B ， C D$ 于点F，E． $∠ D E F$ 的平分线交 $A B$ 于点G．若 $∠ 1 = 50 °$ ，则 $∠ 2 =$ （）

A、 $130 °$ B、 $65 °$ C、 $50 °$ D、 $25 °$

查看试题解析
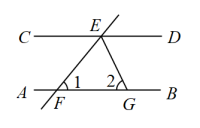5. 代数式 $\frac{5}{\sqrt{x + 1}}$ 有意义时，x应满足的条件为（）

A、 $x > - 1$ B、 $x \geq - 1$ C、 $x < - 1$ D、 $x \neq - 1$

查看试题解析
6. 若关于 $x$ 的一元二次方程 $x^{2} - x + n = 0$ 有两个相等的实数根，则实数n的值为（）

A、4 B、 $\frac{1}{4}$ C、 $- \frac{1}{4}$ D、－4

查看试题解析
7. 《孙子算经》中记载：“凡大数之法，万万曰亿，万万亿曰兆”说明了大数之间的关系：1亿 $=$ 1万 $\times$ 1万，1兆 $=$ 1万 $\times$ 1万 $\times$ 1亿．将“1兆”用科学记数法表示为（）

A、 $1 \times 10^{12}$ B、 $10 \times 10^{15}$ C、 $1 \times 10^{16}$ D、 $0.1 \times 10^{17}$

查看试题解析
8. 如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成第100个图形，则第100个图形需要的小木棒的数量为（）

A、796 B、798 C、800 D、802

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的直径，点C，D在 $⊙ O$ 上，若 $∠ D = 40 °$ ，则 $∠ B A C$ 的度数是（）

A、40° B、45° C、50° D、80°

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A = 90 °$ ，设 $∠ A ， ∠ B ， ∠ C$ 所对的边边长分别为a，b，c，则下列等式正确的是（）

A、 $\tan B = \frac{b}{a}$ B、 $\tan B = \frac{c}{b}$ C、 $\sin B = \frac{a}{b}$ D、 $\sin B = \frac{b}{a}$

查看试题解析
11. 下列说法正确的是（）

A、了解一批新能源电池的使用寿命，可以采用抽样调查的方式 B、如果某彩票的中奖概率是 $2 %$ ，那么一次购买50张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同， $S_{甲}^{2} = 2.3$ ， $S_{乙}^{2} = 4.24$ ，则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子，掷出的点数是0”是必然事件

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A D > A B$ ，连接 $A C$ ，分别以点A，C为圆心，大于 $\frac{1}{2} A C$ 的长为半径画弧，两弧交于点M，N，直线 $M N$ 分别交 $B C ， A D$ 于点E，F．下列结论：
①四边形 $A E C F$ 是菱形；② $∠ C F D = 2 ∠ A C F$ ；③ $A C \cdot E F = C E \cdot A B$ ；④若 $A E$ 平分 $∠ B A C$ ，则 $C E = 2 B E$ ．

其中正确结论的个数是（）

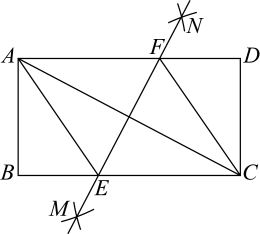A、4 B、3 C、2 D、1

查看试题解析

二、填空题

13. 分解因式： $x y^{2} - x =$ ．

查看试题解析
14. 设 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} + 2 x - 8 = 0$ 的两根，则 $x_{1}^{2} + x_{2}^{2} =$ ．

查看试题解析
15. 已知一个圆锥的底面半径为 $5cm$ ，母线长为 $6cm$ ，则这个圆锥的侧面积为 ${cm}^{2}$ ．

查看试题解析
16. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的一部分如图所示，该函数的图象经过点 $(- 3 ， 0)$ ，对称轴为直线 $x = - 1$ ．对于下列结论：
① $a b c > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a + b + c = 0$ ；④若 $(x_{1} ， y_{1})$ 和 $(x_{2} ， y_{2})$ 均在该函数的图象上，且 $- 1 < x_{1} < x_{2}$ ，则 $y_{1} > y_{2}$ ．

其中正确的结论有．（填序号）

查看试题解析

三、解答题

17. 计算： ${(\sqrt{3})}^{2} + (4 - π) ° - | - 3 | + \sqrt{2} \cos 45 °$ ．

查看试题解析
18. 先化简，再求值： $\frac{a}{a - 1} \div \frac{a + 1}{a^{2} - 1} - (1 - 2 a)$ ，其中 $a = - \frac{1}{3}$ ．

查看试题解析

19. 孔子说“知之者不如好之者，好之者不如乐之者．”兴趣是最好的老师，阅读、书法、绘画、手工、烹饪、运动、音乐……各种兴趣爱好是打开创新之门的金钥匙．某校为了解学生兴趣爱好情况，组织了问卷调查活动，从全校

1500

名学生中随机抽取了

200

人进行调查，其中一项调查内容是学生每周自主发展兴趣爱好的时长，对这项调查结果使用画“正”字的方法进行初步统计，绘制了学生每周自主发展兴趣爱好的时长的频数分布表和频数分布直方图如下：

学生每周自主发展兴趣爱好时长频数分布表

组别	时长t（单位： $h$ ）	人数累计	人数
A	$1 \leq t < 2$	正正正正正正正正	40
B	$2 \leq t < 3$	正正正正正正正正正正	50
C	$3 \leq t < 4$	正正正正正正正正正正正正正正正正	80
D	$4 \leq t < 5$	正正正正正正	30

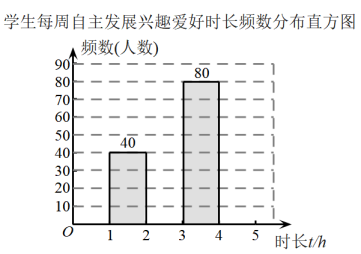
根据以上信息，解答下列问题：

(1)、补全频数分布直方图；

(2)、这

200

名学生每周自主发展兴趣爱好时长的中位数落在组；

(3)、若将上述调查结果绘制成扇形统计图，则B组的学生人数占调查总人数的百分比为，对应的扇形圆心角的度数为；

(4)、学校倡议学生每周自主发展兴趣爱好时长应不少于

2h

，请你估计，该校学生中有多少人需要增加自主发展兴趣爱好时间？

查看试题解析

20. 从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛．

(1)、若甲一定被选中参加比赛，再从其余3名学生中任意选取1名，恰好选中乙的概率是；

(2)、任意选取2名学生参加比赛，求一定有丁的概率．（用树状图或列表的方法求解）

查看试题解析
21. 为深入学习党的二十大精神，某校举办了“学习二十大，奋进新征程”知识竞赛，学校计划购买两种奖品共计30份分别发放给获得一等奖、二等奖的同学，获奖同学各发一份奖品，同一等级奖品相同．设一等奖奖品的单价为x元，购买两种奖品的总费用为y元．

(1)、若购买一等奖、二等奖奖品的单价分别为40元、20元，则学校共需花费800元，求获得一等奖、二等奖的人数分别是多少？

(2)、在（1）的结果下，若一等奖、二等奖奖品的单价的和为60元，一等奖奖品的单价不超过二等奖奖品单价的 $1.5$ 倍，求总费用y的最小值．

查看试题解析
22. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $B C$ 是 $⊙ O$ 的直径，点D是 $⊙ O$ 外一点， $A C$ 平分 $∠ B C D$ ，过点A作直线 $C D$ 的垂线，垂足为点D，连接 $A D$ ，点E是 $A B$ 的中点，连接 $O E$ ．

(1)、求证： $A D$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的直径为10， $O E = 3$ ，求 $C D$ 的长．

查看试题解析
23. 如图①，四边形 $A B C D$ 是正方形，点E是对角线 $A C$ 上一点（点E不与点A，C重合），过点E作 $E F ∥ C D$ ，交BC于点F，作 $E G ∥ B C$ ，交 $C D$ 于点G．

(1)、求证：四边形 $E F C G$ 是正方形；

(2)、如图②，将四边形 $E F C G$ 绕点C顺时针旋转 $α (0 ° < α < 90 °)$ ，连接 $A E$ ， $D G$ ，求 $\frac{A E}{D G}$ 的值．

查看试题解析
24. 已知抛物线 $y = a x^{2} + b x$ 经过点 $(1 ， 1)$ ，关于直线 $x = 1$ 成轴对称．设抛物线 $y = a x^{2} + b x$ 与函数 $y = \frac{- 2}{x}$ 图象的交点（交点也称公共点）的横坐标为d． $m = \frac{d^{9} - 2 d^{8} + d^{6} - 8 d^{5} + 4 d^{4} - 8 d^{2}}{d^{7} - 4 d^{6} + 4 d^{5}}$ ， $n = \frac{1}{d}$ ．

(1)、求抛物线的解析式；

(2)、以下结论： $m > n$ ， $m = n$ ， $m < n$ ，你认为哪个正确？并证明你认为正确的结论．

查看试题解析